
1458
.pdf
|
5,6 |
8, 4 |
11, 4 |
|
14 |
|
|
|
|
|
4, 2 |
8, 2 |
|
|
6 |
|
|
z |
5,8 |
z |
|
u; |
(2.48) |
|||
|
|
10,8 |
16,8 |
|
|
5 |
|
|
|
10, 2 |
|
|
|
|
|||
y 2,8 |
2, 2 |
3, 2 z. |
|
|
|
|
|
|
, x
z ,
y u -
.
2.6.
: -
( ) .
–
( ,
),
.
( ) – ,
-
.
:
.
– , -
, -
, . . -
.
– ,
-
. -
, . .
.
-
.
:
30
– ,
( )
. , .
– ,
, .
, -
-
, .
–
, -
.
,
, -
.
, 1- -
. -
, 2-
. , -
( . . 2.7).
,
-
. , .
-
,
= K + 0. |
(2.49) |
K. -
, ,
. ,
.
, -
-
.
– -
,
.
,
-
, . ,
, – –
.
31
2.7.
,
, -
, .
y = F(x,f), t.
.
-
y
x:
y = F(x ). |
(2.50) |
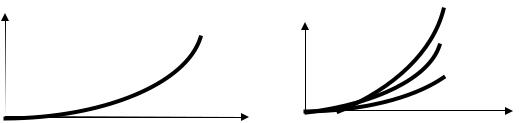
( . 2.6, )
y ( ).
f,
y = F(x)
f ( . 2.6, ), y = F(f) x.
) |
|
) |
f3 |
|
|
||
|
|
f2 |
|
|
|
||
|
|
|
f1 |
|
|
|
|
. 2.6.
.
y = Kx. , -
( ) K . -
K = y/u,
. -
( -
), ( . . 2.11).
32
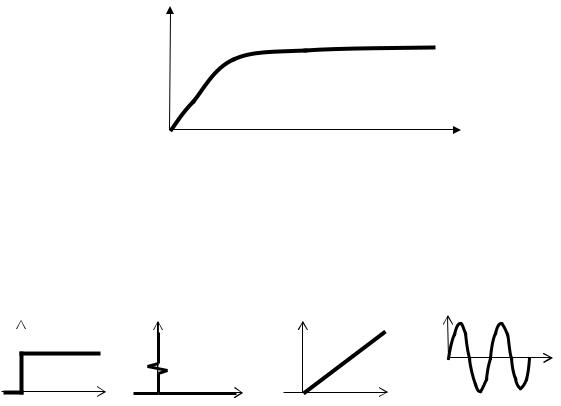
. -
, -
, .
y(t) ( . 2.7).




t
. 2.7.
, .
( . 2.8).
x |
x |
x |
x |
1 |
|
t |
|
|
|
t |
t |
t |
) |
) |
) |
) |
|
, |
|
) |
|
) |
|
|
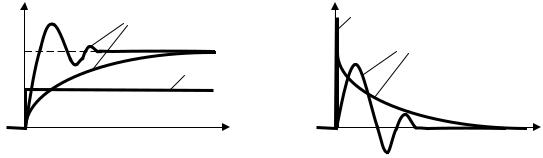
. 2.8.
( , -
, , -
) – , -
– .
1(t)
0, t 0; |
(2.51) |
1(t) |
|
1, t 0. |
|
33
( , ) – -
, , -
( ,
.). -
.
(t)
|
, t 0; |
(2.52) |
|||
|
(t) |
||||
|
0, t 0. |
|
|||
|
|
d1(t) |
|
|
|
(t)dt 1(t) (t) |
. |
(2.53) |
|||
|
|||||
|
|
dt |
|
||
(t)
:
h(t) -
-
(t) x(t) = 1(t)
, . . (0) = 0 (0) = 0 ( . 2.9, ).
w(t) -
-
, . .
(0) = 0 (0) = 0 ( . 2.9, ).
y |
h(t) |
) |
y |
x(t) = (t) |
) |
w(t)
x(t) = 1(t)
t |
t |
. 2.9. :) h(t);
) w(t)
, -
.
34
-
, ,
, -
.
-
y(t), -
x(t).
x(t ) xmax sin t; |
(2.54) |
|
|
y (t ) ymax sin( t ), |
|
xmax, ymax – , – |
, |
– .
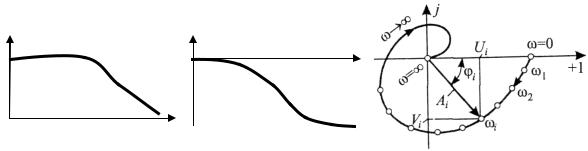
( ) – -
A = ymax/xmax ( . 2.10, ).
( ) –
. 2.10, ).
( ) –
, [+1; j]
( . 2.10, ), -
. -
Ai , i .
.
) |
) |
) |
|
|
|
|
|
. 2.10. :) ; ) ; )
–
, ( . 2.11).
35
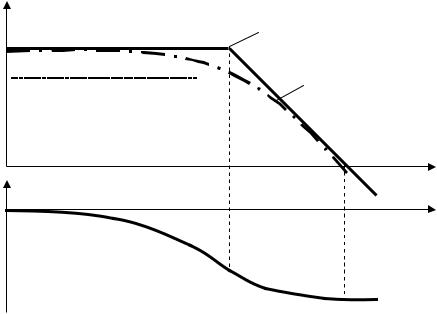
L,
20lgK
lg
, |
0 |
|
|
|
lg
. 2.11.
– L = f(lg ), – = f(lg ).
L lg :
lg b , 10b ; |
(2.55) |
L 20 lg A . |
(2.56) |
L [ ].
– , -
.
1 = 10 – 10 . 2 = 20 – 100 ;
3 = 30 – 1000 .
lg [ ].
– ,
10 .
-
.
– , -
( ).
-
:
L = 20lgK lg = 0 ( = 1) – ,
K – ;
36
0 – ,
;
– – L ;
[ ].
2.10.
-
. -
, . .
Y(p) X(p)
:
W ( p) |
Y ( p) |
. |
(2.57) |
|
|||
|
X ( p) |
|
|
-
|
B( p) |
|
b p m b p m 1 |
b p m 2 |
... b |
|
||
W ( p) |
|
|
0 |
1 |
2 |
m |
, |
(2.58) |
|
a0 p n a1 p n 1 |
|
|
|||||
|
A( p) |
|
a2 p n 2 ... an |
|
||||
B(p) = b0 pm + b1 pm-1 + b2 pm-2 + … + bm – ,(p) = a0 pn + a1 pn-1 + a2 pn-2 + … + an – .
,
n. (2.57) , -
Y(p) = W(p X(p). |
(2.59) |
X -F ( . 2.1) ( )
:
F(p) = 0, A( p) Y ( p) B( p) X ( p) ;
X(p) = 0, A( p) Y ( p) Q( p) F ( p) .
, , -
,
WX |
( p) |
Y ( p) |
|
B( p) |
; |
(2.60) |
X ( p) |
|
|||||
|
|
|
A( p) |
|
||
37
WF |
( p) |
Y ( p) |
|
Q( p) |
. |
(2.61) |
F ( p) |
|
|||||
|
|
|
A( p) |
|
||
(2.60)
, (2.61) -
.
(2.60) (2.61).
2.11.
, -
.
:
;
;
.
,
.
.
, -
-
.
,
.
,
. -, .
:
;
;
;
;
;
;
.
38
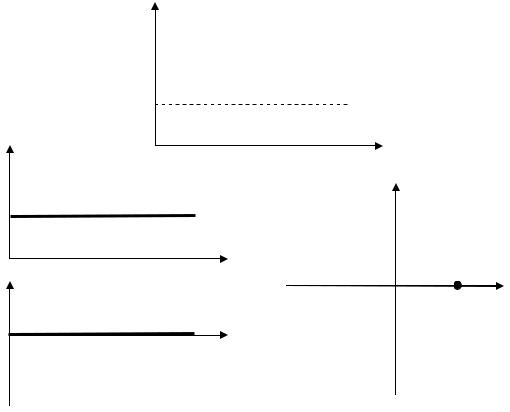
x K . K -
. -
,
.
:
= K· . |
(2.62) |
|
(2.63) |
W(p) = K. |
|
( . 2.12, ) |
|
h(t) =K 1(t). |
(2.64) |
( . 2.12, ) |
|
A K ; |
(2.65) |
L 20 lg K ; |
(2.66) |
0 . |
(2.67) |
, [+1; j],
, ( . 2.12, ).
|
h(t) |
) |
|
|
|
K |
|
|
|
|
|
|
|
|
|
x = 1(t) |
|
|
|
L, |
0 |
|
t |
|
|
|
|
||
|
|
|
) |
|
|
) |
|
|
|
|
jV( ) |
|
||
20 lg K |
|
|
||
|
|
|
|
|
0 |
|
lg |
|
|
|
|
|
K |
|
, |
|
|
|
|
|
0 |
U( ) |
||
|
|
|||
|
|
|
|
|
0 |
|
lg |
|
|
|
|
|
||
. 2.12. :) ; ) ; )
39
