
1458
.pdf
|
|
|
. 2.1 |
||||
|
|
|
|
|
|
|
|
f (x) |
f '(x) |
||||||
tg x |
|
|
|
1 |
|
|
|
|
cos2 x |
|
|||||
|
|
|
|||||
ctg x |
|
|
|
1 |
|
|
|
|
sin2 x |
|
|||||
|
|
|
|||||
arcsin x |
|
|
|
1 |
|
|
|
|
1 x2 |
|
|||||
|
|
|
|||||
arccos x |
|
1 |
|
|
|
||
|
|
|
|
||||
|
|
|
1 x2 |
|
|||
arctg x |
|
|
|
1 |
|
|
|
|
1 x2 |
|
|||||
|
|
|
|||||
arcctg x |
|
|
1 |
|
|
|
|
|
x2 |
|
|||||
|
1 |
|
|||||
: |
|||||||
F 3xy 4x2 1,5xy 5 y y 0 . |
(2.7) |
||||||
-
. -
x0 1, x0 0 , y0 0 .
0 -
: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 0 – 4 + 0 = 0 + 0. |
(2.8) |
|||||||||||||
0 = 2. - |
|||||||||||||||||||||||
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
F |
|
|
|
3 y 8x |
|
0 |
|
|
3 2 8 1 2 ; |
(2.9) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
F |
|
|
x |
0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3x 1,5x 1 |
|
0 |
3 1 1,5 0 1 2 ; |
(2.10) |
|||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
0 |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1,5 y |
|
1,5 2 3 ; |
(2.11) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
0 |
F |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 . |
(2.12) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
20

, ,
(2.6):
5 y 2 y 3 x 2 x 0 . |
(2.13) |
2.4.
.
, -
a |
|
d 2 y |
a |
dy |
a |
|
y b |
dx |
b x , |
(2.14) |
|
0 dt |
|
|
|
|
|||||||
|
2 |
1 dt |
|
2 |
0 dt |
1 |
|
||||
– .
x(t) y(t) X(p) Y(p) -
p, , :
|
|
|
X ( p) x(t)e pt dt Y ( p) y(t)e pt dt , |
(2.15) |
|
0 |
0 |
|
a0 p2 Y(p) + a1 p Y(p) + a2 Y(p) = b0 p X(p) + b1 X(p); |
|
(2.16) |
|||||
p |
d |
. |
|
|
|
(2.17) |
|
|
|
|
|
||||
|
dt |
|
|
|
|
||
- |
|||||||
|
|
|
d n |
n |
|
|
|
|
|
p |
, |
|
|||
dtn |
|||||||
|
|
|
|
|
|
||
...dt 1 , x(t) y(t) – - p
X(p) Y(p).
-
,
(2.15) – ,
–
.
21

|
|
L x(t) X p . |
(2.18) |
x(t) , X(p) – .
.
x(t) L 1 X ( p) |
1 |
|
|
|
X ( p)e pt dt . |
(2.19) |
|||
|
||||
|
2 |
|
||
,
( . 2.2),
X(p) x(t). -
,
.
(2.15) (2.19).
2.2
|
x(t) X(p) |
|
(t ) e p |
|
1(t)(t ) |
e p |
|
||||||||||||||
|
|
p |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
t |
n |
|
|
n! |
|
|
|
|
|
|
|||||
|
|
p |
n 1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1(t) |
1 |
|
|
|
|
|
|
|
|||||||
|
p |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
» |
1(t)t |
1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
p2 |
|||||||||
|
1(t) t 2 |
2 |
|
|
|||||||||||||
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|||||||
|
1(t) t3 |
6 |
|
|
|||||||||||||
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|||||||
|
Me |
t |
|
|
|
|
M |
||||||||||
|
|
p |
|
||||||||||||||
= const |
x(t) X(p) |
||||||||||||||||
22

|
|
|
|
|
|
|
|
|
. 2.2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x(t) X(p) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
xi (t) Xi ( p) |
||||||||||||||
|
|
|
|
|
|
|
|
i 1 |
i 1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
d n x(t) |
p |
n |
|
X ( p) |
|||||||||||
|
|
|
|
dt n |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
X ( p) |
|
|
|
||||
|
|
|
|
|
|
x(t)dt |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
sin( t) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
p |
2 |
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
cos( t) |
|
|
|
|
|
p |
|
|
|
|
|||
|
|
|
|
|
|
|
p |
2 |
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
d 2 y |
5 |
dy |
6 y 2 |
dx |
12x . |
|
|
|
|
|
|
|
|
|
(2.20) |
||||
|
dt 2 |
dt |
dt |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
, -
, . . x(t) = 1(t).
X(p) = 1/ .
X(p) Y(p): |
|
p2 Y(p) + 5 p Y(p) + 6 Y(p) = 2 p X(p) + 12 X(p), |
(2.21) |
p2 Y(p) + 5 p Y(p) + 6 Y(p) = 2 p 1 + 12 1 , p p
Y(p (p3 + 5 p2 + 6 p) = 2 p + 12.
Y:
Y p |
2 p 12 |
|
|
. |
|
p3 5 p2 6 p |
||
(2.22)
(2.23)
(2.24)
-
.
,
p(p + 2)(p + 3):
Y p |
2 p 12 |
|
|
2 p 12 |
|
2 |
|
4 |
|
2 |
|
. (2.25) |
p3 5 p2 |
|
p( p 2)( p 3) |
|
|
p 3 |
|||||||
|
6 p |
|
p |
p 2 |
|
|||||||
23
, ,
|
|
y(t) = 2 – 4 e-2t + 2 e-3t. |
(2.26) |
,
, .
,
) -
1- ( ) -
– .
xi(t) (n–1) -
y(t).
.
x (t) y(i 1) |
(t), i 1, 2...n . |
(2.27) |
i |
|
|
– n
, -
-
. -
( )
-
.
) y -
xi(t) , y(t)
t = t1 > t0
xi0 = xi(t0).
, . .
u(t) -
y(t). xi
–
24
t1 > t0 -
xi0
[t0; t1] u = u[t0; t1].
. 2.3) :
x x1 , x2 ... |
xn T , |
(2.28) |
( ) |
|
|
u u1 ,u2 ... |
um T , |
(2.29) |
|
|
|
f f1,f2 ... |
fl T , |
(2.30) |
|
|
y y1 , y2 ... |
yk T . |
(2.31) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
x |
y |
||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
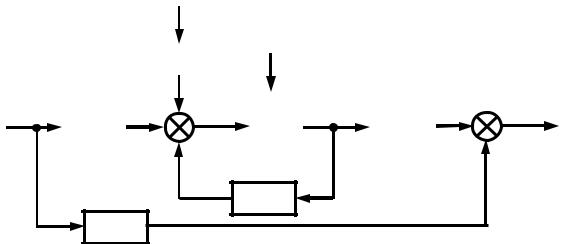
. 2.3.
x -
,
. -
n .
m , l , k n
-
1- :
25
x1 a11x1 a12 x2 ... a1n xn b11u b12u ... b1mu q11 f ... q1l f ; |
|
|||||||||||||||||||||||||
x |
|
a x a |
|
x |
... a |
|
|
x |
b u b |
|
|
u ... b |
|
|
u q |
21 |
f ... q |
2l |
f ; |
|||||||
2 |
21 1 |
|
22 2 |
|
|
2n n |
|
21 |
22 |
|
2 m |
|
|
|
|
|||||||||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1x1 |
an2 x2 ... ann xn bn1u bn2u ... bnmu qn1 f ... qnl f ; (2.32) |
|||||||||||||||||||||||
xn |
||||||||||||||||||||||||||
y |
|
c x |
c |
|
x ... c |
|
|
x |
n |
d |
u |
d |
|
u |
... d |
|
u; |
|
|
|
|
|||||
1 |
11 1 |
12 2 |
1n |
|
|
11 |
12 |
|
|
1m |
|
|
|
|
|
|
|
|||||||||
y |
|
c x |
c |
|
x |
... c |
|
|
x |
d u d |
|
|
|
u ... d |
|
|
|
u; |
|
|
|
|
||||
|
2 |
21 1 |
22 2 |
|
2n n |
|
21 |
|
22 |
|
2 m |
|
|
|
|
|
||||||||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
k |
c x |
c |
|
x |
... c |
|
x |
n |
d |
u d |
k 2 |
u ... d |
km |
u. |
|
|
|
|
|||||||
|
k1 1 |
k |
2 2 |
|
kn |
|
|
k1 |
|
|
|
|
|
|
|
|||||||||||
|
|
(2.32) - |
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x Ax Bu Qf ; |
|
|
|
|
|
|
|
(2.33) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
y Cx Du, |
|
|
|
|
|
|
|
|
|||||||
– , – -
, Q – n l,
– , D –
m.
,
, (2.33) -
y
y C Ax Bu Qf Du , |
(2.34) |
p |
|
. 2.4, x0 – -
.
Q D , ,
.
m = 1, k =1 n , ,, D, Q
a11 |
a12 |
... |
a1n |
b1 |
|
|
|
|
|
|
|
|||
a |
a |
... |
a |
|
|
b |
|
|
c |
c |
|
, D 0 |
,Q 0 . (2.35) |
|
A |
21 |
22 |
|
|
2n , B 2 |
, c |
n |
|||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
||
|
|
an2 |
... |
|
|
|
|
|
|
|
|
|
|
|
an1 |
ann |
bn |
|
|
|
|
|
|
|
|||||
26
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Q) |
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u |
|
|
|
|
. |
|
|
|
x |
|
y |
|
+ |
|
1 |
|
|
||||||||
+ |
|
x |
|
|
||||||||
|
(B) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(C) |
|
|
|
+ |
|
|
|
p |
|
|
+ + |
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
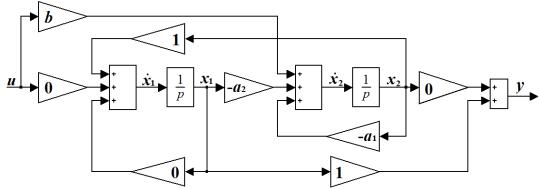
(A)
(D)
. 2.4. ,
-
, ( -
) . -
z, -
z = Px, |
(2.36) |
– , n n,
, . . det P 0.
-
z Az Bu; |
||
|
|
|
|
|
(2.37) |
y Cz, |
|
|
|
|
|
1 |
; |
|
|
A PAP |
|
|
||
|
|
|
|
(2.38) |
|
B PB; |
|
|
|||
|
|
1 |
. |
|
|
C CP |
|
|
|
||
-
. -
. y
u .
27
-
, -
2- :
y a1 y a2 y bu |
(2.39) |
u – , y – , ai, b – -
.
(2.27),
, (n–1) y(i–1)
xi:
x1 y , x2 y |
(2.40) |
: |
|
x1 y x2 ; |
(2.41) |
x2 y bu a1 y a2 y bu a1x2 a2 x1 |
(2.42) |
-
(2.32)
x1 x2 ;
x2 a2 x1 a1x2 bu; (2.43)
y x1.
(2.43) :
|
0 |
|
1 |
|
0 |
|
|
|||
x |
|
a |
|
a |
x |
b |
u; |
(2.44) |
||
|
|
2 |
|
|
|
|||||
|
1 |
|
|
|||||||
|
|
|
0 |
x. |
|
|
|
|
|
|
y 1 |
|
|
|
|
|
|||||
(2.43), -
, . 2.5.
. 2.5.
28
-
, -
1- :
x1 x1 u; |
|
|
||
|
2x2 x3 5u; |
|
||
x2 |
(2.45) |
|||
x |
4x |
x |
4x ; |
|
3 |
1 |
2 |
3 |
|
y 2x |
x . |
|
|
|
|
2 |
3 |
|
|
(2.45):
|
|
1 0 0 |
1 |
|
|||||
|
|
|
0 |
2 1 |
|
|
5 |
|
|
x |
|
x |
|
u; |
(2.46) |
||||
|
|
|
4 |
1 4 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
y 0 2 1 x.
|
1 |
3 |
0 |
|
|
P |
|
6 |
0 |
|
(2.47) |
|
1 . |
||||
|
|
5 |
2 |
|
|
|
|
1 |
|
||
-
(2.46), (2.38).
-
MS Excel
:
( A) "= (A16:C18;A3:C5);( (A16:C18)))" "= (A16:C18;A8:A10)"
(C) "= (A13:C13; (A16:C18))"
:
( ) = {A3:C5}, (B) = {A8:A10}, (C) = {A13:C13}, (P) = {A16:C18}.
, ,
-
(
), F2,
Ctrl+Shift+Enter.
29
