
1458
.pdf1.4.
,
, -
.
1.:
;
;
.
2.:
– , -
-
(X = const);
– ,
(X -);
– , -
-
(X = var).
3. . . 2.6):
– -
-
;
–
.
4. :
– ;
– .
5. :
– ;
– -
.
:
) , -
;
10
) ,
-
.
6. :
–
;
, , ) –
.
-
, ,
, .
7. :
;
;
;
.
8.:
;
.
9.:
;
.
-
. -
.
.
-
, -
.
1. :
;
;
;
.
11
2. , :
;
;
;
;
.
3. -
:
( );
( ).
4.:
;
.
5.. . 2.6):
– , -
(
). ;
– .
: -
.
.
, -
. -
.
.
( . 1.5). -
,
, , -
, -
.
, -
,
. -
12
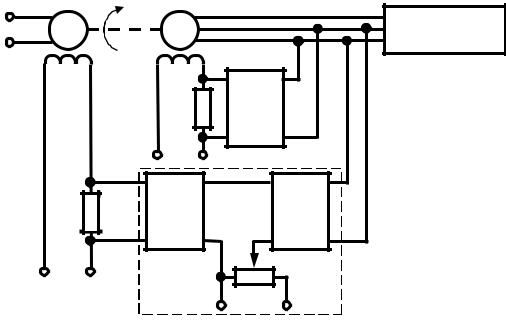
. , -
, ,
.
-,
(
) ( -
).
. -
.
– U |
|
|
|
|
|
|
|
– U |
|
|
|
|
|
– U |
|
R |
|
|
|
|
– U |
|
|
|
. 1.5.
, , -
-
( . 1.6).
(
), R , -
, , -
13
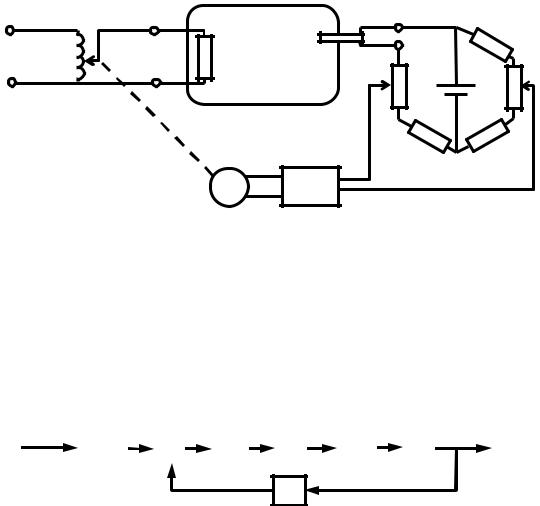
.
, . -
R ,
, .
, -
. , , -
, -
, -
. , , -
.
|
|
|
RT |
~ U |
|
|
|
|
|
|
R |
|
|
G |
|
|
|
|
. 1.6.
, . 1.7.
|
|
|
|
|
|
|
|
|
|
|
Y ( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
) |
R |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
R
Y' (
)
. 1.7.
14
?
2.?
3..
4.?
.
5.? -
?
6.?
.
7..
8.-
?
9..
.
11.-
.
15

2.
2.1.
– -
, -
.
, , (
) .
, -
, . . .
. -
, -
.
-
. -
, . -
,
. -
, -
, . . , . .
2.2.
,
, f y . 2.1). -
.
|
f |
|
|
|
y |
x |
|
|
|
|
|
. 2.1.
16
– , -
. -
. ,
.
.
,
-
, ,
.
( -
)
, ,
.
2.3. .
, -
-
,
, .
-
,
, .
–
, .
, .
.
-
,
F (x, x, x,....., y, y, y,.....) 0. |
(2.1) |
, -
.
-
.
17
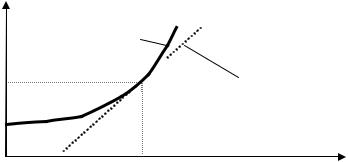
, -
-
, -
,
.
-
F( , ) = 0 ( 0, 0) -
. 2.2),
F |
x |
F |
y 0 . |
(2.2) |
x |
|
|||
|
y |
|
||
y
y0 
x0 |
x |
. 2.2.
, -
y = f(x),
0, y0.
, ( 0, y0) ,
,
|
|
|
df |
|
||
|
|
y |
f (x0) |
|
(x x0), |
(2.3) |
|
|
|
||||
|
|
|
dx 0 |
|
||
: |
df |
– x |
||||
|
||||||
dx 0 |
|
|
|
|
||
x = x0). |
|
|||||
(2.3) |
|
|||||
|
|
|
y f (x0) k x ; |
(2.4) |
||
|
|
|
y k x . |
(2.5) |
||
18

, -
= – 0
= – 0.
( 0, y0). k -
: k tg .
(2.1)
, , -
F
x
|
F |
||
|
x |
|
|
x |
|||
0 |
|
||
|
F |
||
|
x ... |
|
|
y |
|||
0 |
|
||
|
F |
|
|||
|
y |
|
|
y ... 0 , (2.6) |
|
y |
|||||
0 |
|
0 |
|
||
|
F |
, |
F |
|
, …, |
F |
– - |
|
|
|
|||||
x |
0 x 0 |
y |
0 |
||||
.
. 2.1
.
|
|
|
|
|
|
2.1 |
||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f (x) |
|
|
f '(x) |
||||||||||||||
|
|
g(x) |
|
|
|
|
|
|
g' (x) |
|
||||||||
|
g(x) ± q(x) |
|
|
|
|
g' (x) ± q' (x) |
|
|||||||||||
|
g(x q(x) |
|
|
g' (x q(x) + g(x q' (x) |
||||||||||||||
|
|
|
g (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
g (x)q(x) g(x)q (x) |
, q(x) 0 |
|||||||||||||
|
|
|
q(x) |
|
|
|
q2 (x) |
|
|
|
||||||||
|
C |
, const |
|
|
|
|
Cq (x) |
, q(x) 0 |
||||||||||
|
|
|
|
|
|
|
||||||||||||
|
q(x) |
|
|
|
|
|
|
|
q2 (x) |
|
|
|
||||||
|
g(x) |
q(x) |
|
q( x) |
|
q(x) |
|
|
|
|
||||||||
|
|
|
g(x) |
g (x) |
|
|
|
|
q |
(x) ln g(x) , g(x) 0 |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
g(x) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
= const |
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
|
|
|
|
|
|
x -1 |
|
|||||||
|
|
|
C x |
|
|
|
|
|
|
C x lnC |
|
|||||||
|
|
log c x |
|
|
|
|
1 |
|
|
, x 0,C |
1 |
|||||||
|
|
|
|
|
x ln C |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
sin x |
|
|
|
|
|
|
|
|
cos x |
|
|||||
|
|
cos x |
|
|
|
|
|
|
- sin x |
|
||||||||
19
