Тема 10
Метод множеств в решении геометрических задач на построение
Вопросы для самопроверки
1.Назвать геометрическое множество точек, удаленных от данной точки на расстояние R.
2.Назвать геометрическое множество точек, удаленных от данной прямой на расстояние R.
3.Назвать геометрическое множество точек, равноудаленных от двух данных точек.
4.Назвать геометрическое множество прямых, проходящих через данную точку и данную прямую.
5.Назвать геометрическое множество прямых, проходящих через данную точку и удаленных от другой точки на расстояние R.
6.Назвать геометрическое множество прямых, проходящих через данную точку и перпендикулярных данной прямой.
7.Назвать геометрическое множество прямых, проходящих через
данную точку и наклоненных к данной плоскости под углом ϕ.
_________________________________________________________________________________________________________________
Суть метода множеств
Пусть требуется построить фигуру Х, удовлетворяющую ряду требований, например Т1, Т2.
1.Рассматривают одно из требований, например Т1, и строят в этих ограниченных условиях фигуру Х1, которая является множеством искомой
Х.
2.Рассматривают другое требование Т2 и строят по требованию Т2 множество искомых Х, образующее фигуру Х2.
3.Искомая фигура Х находится как пересечение вспомогательных
фигур Х1 и Х2:
Х = Х1 ∩Х2
ПРИМЕР. На прямой с найти точку Х, равноудаленную от точек А и В.
Анализ условия
В задаче два требования:
1.Т1 – точка Х равноудалена от точек А и В.
2.Т2 – точка Х принадлежит прямой с.
38
Решение |
|
12 |
|
|
Х2 |
|
|
|
|
|||||
1. |
Множество Х1 то- |
|
|
с2 |
||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
||||||||
чек Х по Т1 есть срединная |
|
А2 |
|
|
|
|
|
22 |
|
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||
плоскость δ |
плоскость, |
|
|
|
|
|
|
|
|
|
|
|
||
проходящая |
через середину |
|
|
|
|
|
|
|
В2 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
отрезка АВ и перпендику- |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
лярная ему. |
|
|
х1 2 |
|
|
|
|
|
|
|
|
|
|
|
2. |
Множество Х2 |
то- |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
21 |
|
|||||
чек Х по Т2 есть прямая |
с. |
|
|
|
|
|
|
с1 |
|
В1 |
||||
3. |
Искомая точка Х |
|
|
|
|
|
|
Х1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
строится как точка пересе- |
11 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||
чения прямой с с плоско- |
|
|
|
|
|
В3 |
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||
стью δ : |
|
|
|
|
|
|
|
|
|
|
23 |
|||
|
Х = с ∩δ |
|
|
А1 |
|
|
|
|
|
|
|
с |
||
|
|
|
|
|
|
|
|
|
||||||
|
|
3 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
х1 |
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
13 |
Х3 |
|||||
|
|
|
|
|
|
|
А3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
B |
c |
X
δ
A
39
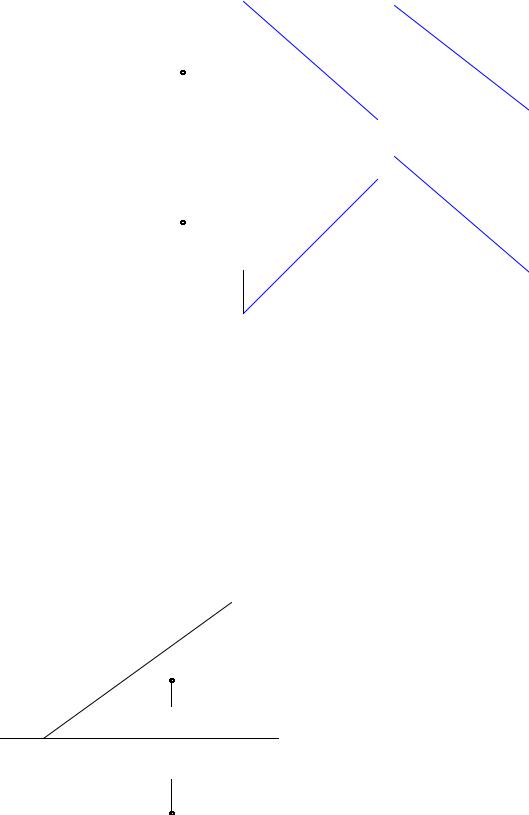
51. |
Построить |
|
|
|
|
b2 |
|
c2 |
|
прямую х, проходящую |
|
|
|
|
|
|
|
|
|
через точку А и пересе- |
|
|
|
|
|
|
|
|
|
кающую |
скре- |
А2 |
|
|
|
||||
щивающиеся прямые b |
|
|
|
||||||
|
|
|
|
|
|
|
|
||
и с. |
х1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
c1 |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
А1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
b1
52. Построить горизонтальный след h0 плоскости α (h0, f0), удаленной от точки А на расстояние 15 мм.
f20
А2
х1 2
А1
40
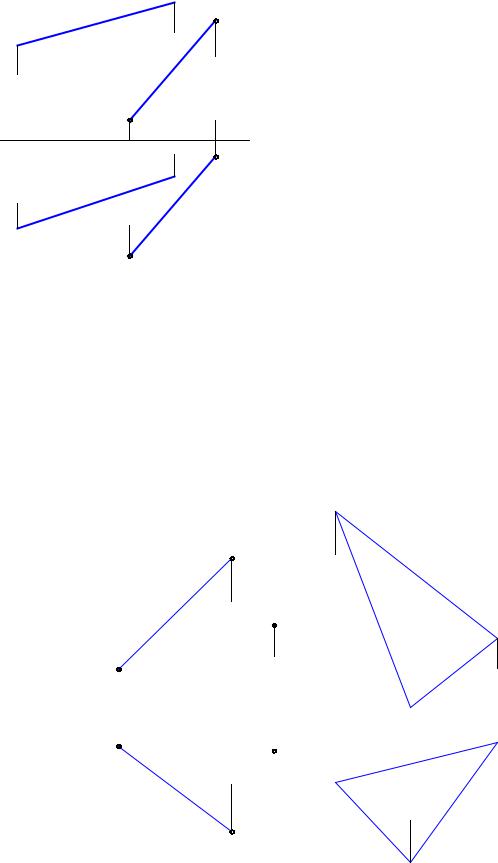
53. На прямой с найти точки S, T, удаленные от прямой АВ на расстояние 20 мм.
с2 А2
В2
х1 2 |
А1 |
|
с1
В1
54.Через точку А провести прямую х, параллельную плоскости KLM
ипересекающую ВС.
М2
С2
А2
L2
|
В2 |
|
|
|
|
К |
||
|
|
|
|
|||||
|
|
|
|
|
|
|||
х1 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
А1 |
|
|
L1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
В1 |
|
М1 |
|||||
|
|
|||||||
|
|
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
С1
К1
41