
- •Принятые обозначения
- •Краткая запись основных операций
- •Основная литература
- •Дополнительная литература
- •Тема 4
- •Тема 10
- •Метод множеств в решении геометрических задач на построение
- •Вопросы для самопроверки
- •Суть метода множеств
- •Анализ условия
- •Решение
- •53. На прямой с найти точки S, T, удаленные от прямой АВ на расстояние 20 мм.
- •55. Построить прямую х, параллельную прямой с и пересекающую скрещивающиеся прямые а и b.

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Сибирская государственная автомобильно-дорожная академия (СибАДИ)»
Кафедра «Начертательная геометрия, инженерная и машинная графика»
О.А. Мусиенко, И.И. Ширлина
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Рабочая тетрадь для практических занятий
Издание второе, исправленное
Студента_____________________________
Группы______________________________
Преподаватель________________________
Омск - 2016
УДК 515 (075.8) |
Согласно 436-Ф3 от 29.12.2010 «О защите детей от |
ББК 22.151.34 |
информации, причиняющей вред их здоровью и |
М 91 |
развитию» данная продукция маркировке не |
|
подлежит. |
Рецензент
д-р техн. наук, проф. С.А. Матвеев (СибАДИ)
Работа утверждена редакционно-издательским советом СибАДИ в качестве рабочей тетради для практических занятий.
Мусиенко, Ольга Алексеевна.
М91 Начертательная геометрия : рабочая тетрадь для практических занятий / О.А. Мусиенко, И.И. Ширлина. – Изд. 2-е, испр. – Омск : СибАДИ, 2016. – 52 с.
ISBN 978-5-93204-923-5.
Собраны задачи для освоения на практике теоретического курса начертательной геометрии, предварительно изложенного в лекциях. Предназначена для непосредственного в ней решения задач обучающимися первого курса направлений и специальностей транспортного строительства.
УДК 515 (075.8) ББК 22.151.34
ISBN 978-5-93204-923-5 |
© ФГБОУ ВПО «СибАДИ», 2014 |
|
© ФГБОУ ВО «СибАДИ», 2016 |
ВВЕДЕНИЕ
Начертательная геометрия, изучающая способы изображения пространственных форм на плоскости, нашла широкое практическое применение в конструкторской практике, в черчении и других технических дисциплинах при решении инженерных задач графическими методами.
В инженерной практике геометрические модели изучаются с помощью чертежей, которые являются средством общения людей в их производственной деятельности. Изображения, построенные по правилам, изучаемым в начертательной геометрии, позволяют представить мысленно форму предметов и их взаимное расположение в пространстве, определить размеры и исследовать геометрические свойства изображаемого предмета.
Изучение курса начертательной геометрии включает обязательное прослушивание лекций, проработку темы лекции с помощью учебника, самостоятельное решение задач данного пособия, написание контрольных работ и выполнение графических работ по индивидуальным заданиям. Задачи каждой темы выполняются карандашом с помощью чертежных инструментов непосредственно в данной рабочей тетради.
После этого студент допускается к сдаче экзамена.
Принятые обозначения
1.Точки в пространстве – прописными буквами латинского алфавита А, В, С,…, а также цифрами 1, 2, 3,…
2.Прямые и кривые линии пространства – строчными буквами латинского алфавита – a, b, c, d…
3.Плоскости – строчными буквами греческого алфавита α, β, γ, δ …
Плоскости проекции – π1, π2, π3… 4. Проекции точек, линий и плоскостей обозначают теми же буква-
ми, что и оригиналы, с добавлением индекса, соответствующего индексу плоскости проекций, например, А1, А2, А3, а1, а2, а3.
Краткая запись основных операций
≡ – совпадение двух геометрических элементов;
• – скрещивающиеся прямые; ∩ – знак пересечения двух элементов;– знак объединения; // – параллельность элементов;
– перпендикулярность элементов;– знак принадлежности элемента множеству;
– принадлежность подмножества множеству;– логическое следствие;– знак "касательно".
3
Например, выражение α (а || b) ∩ m = А означает, что плоскость α, заданная параллельными прямыми а и b пересекается с прямой m в точке А.
Основная литература
1.Начертательная геометрия / под ред. Н.Н. Крылова. – М. : Высшая школа, 2007.
2.Гордон, В.О. Курс начертательной геометрии / В.О. Гордон, М.А. Семенцов-Огиевский. – М. : Высшая школа, 2003.
3.Третьяк, О.М. Инженерное сооружение в проекциях с числовыми отметками : учебно-методическое пособие / О.М. Третьяк, О.А. Мусиенко, Л.Ф. Константинова. – Омск : СибАДИ, 2009.
Дополнительная литература
1. Гордон, В.О. Сборник задач по курсу начертательной геометрии : учеб. пособие для втузов / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева; под ред. Ю.Б. Иванова. – 7-е изд., стер. – М. : Высшая школа, 2004.
Условия защиты тем и графических работ
Каждая тема по начертательной геометрии должна быть освоена студентом с помощью лекций и по учебнику, задачи по теме самостоятельно решены к соответствующему занятию непосредственно в данной тетради с помощью простого карандаша и чертежных инструментов.
На занятии после проверки задач преподавателем студент исправляет выявленные ошибки и защищает тему. Во время защиты оценивается знание терминологии геометрических объектов (всех линий чертежа), правильное изображение изучаемых геометрических объектов на чертеже, грамотное использование способов решения задач на построение, и аккуратность графического исполнения. По окончанию занятия предлагаются тесты по теме. Защищенная тема подписывается и студентом, и преподавателем.
Графические работы выполняются студентом по индивидуальным заданиям на листах ватмана формата А3 карандашом с помощью чертежных инструментов. После проверки работы преподавателем во время консультаций и исправления студентом ошибок, выполняется отмывка объектов на чертеже. При защите работы студент должен представить классификацию исходных данных своей графической работы, способы решения графической задачи и доказать правильность своего решения.
Условия рейтинговой оценки текущей работы должны быть зафиксированы студентом на последних страницах данной тетради. Рейтинговая оценка учитывает не только качество и самостоятельность выполненных работ, но и сроки их выполнения.
4

Тема 1
Комплексный чертеж точки. Координаты. Принадлежность точки прямой. Положение прямой относительно плоскости проекций
Вопросы для самопроверки
1.Что такое комплексный чертеж точки, как он образуется? Как направлены на комплексном чертеже ось x, ось y, ось z?
2.Что называют координатами точки?
3.Какими координатами определяется горизонтальная, какими фронтальная проекция точки?
4.Какая прямая называется прямой общего положения, уровня, проецирующей?
5.Какая прямая называется горизонталью, фронталью, профильной прямой? Как расположены их проекции?
6.Как на комплексном чертеже определяется принадлежность точки прямой?
________________________________________________________________
1. По наглядному изображению построить комплексный чертеж точек А, В, С, D, записать их координаты и четверти пространства, которым они принадлежат.
A(_______________),
B(_______________),
C(_______________),
D(_______________)
5
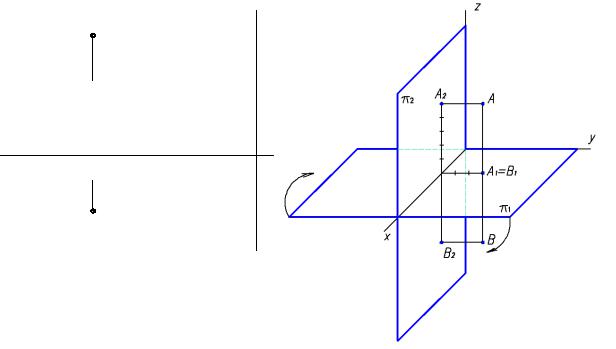
2. По координатам точек A, B, C, D, E, F построить их проекции на плоскости π1, π2. Определить четверти пространства, в которых расположены точки.
A (10, 20, 20) |
- |
|
|
|
B (20, 15, -25) |
- |
|
|
|
C (30, -20, 10) |
- |
|
|
0 |
|
|
|||
|
|
|
||
D (40, 0, 30) |
- |
x1 2 |
|
|
|
|
|||
E (50, -20, -30) - |
|
|
|
|
|
|
|
||
F (60, 30, 10) |
- |
|
|
|
3. Построить проекции точки В, симметричной точке А относительно плоскости π1. Записать координаты точек и их положение в четвертях пространства.
z
А2
x
А1
y
А ( |
, |
, |
), |
В ( |
, |
, |
) |
|
|
|
|
6
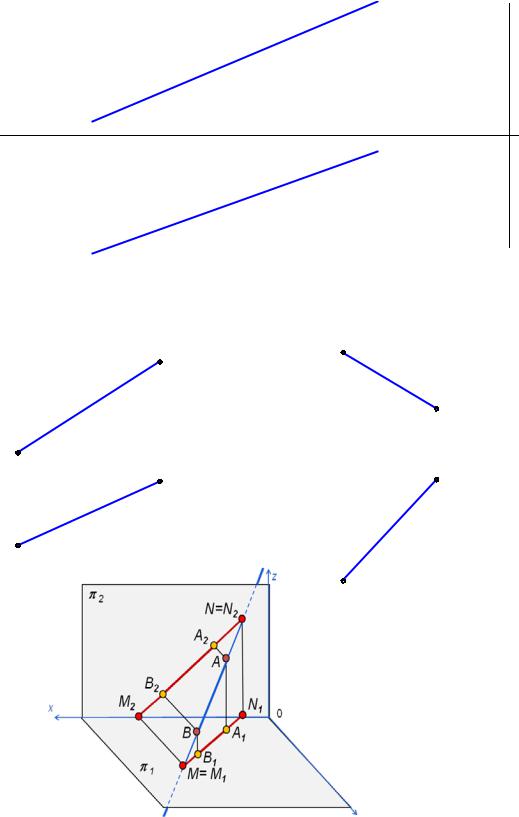
4. На прямой l построить проекции точек А (__, __, 25), В (__,20,__), С (60, __, __), D (__, __, 0) и определить недостающие координаты.
l2
x1 2 0 l1
5.Построить горизонтальный М и фронтальный N следы прямой АВ
иопределить через какие четверти пространства она проходит.
|
|
|
В2 |
|
|
А2 |
|||
|
|
|
|
|
|
В2 |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
А2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
x1 2 |
|
x1 2 |
В1 |
||||||
|
|
|
|
|
|||||
А1 |
|
|
В1 |
|
|
А1 |
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
7
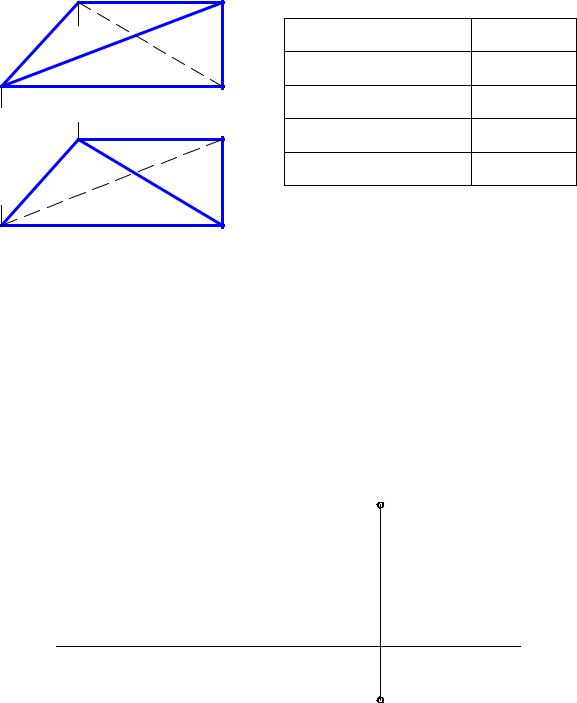
6. Определить из каких отрезков составлена фигура 1234.
12 |
22 |
42 |
32 |
11 |
31 |
41 |
21 |
Прямая Отрезок
Общего положения
Горизонталь
Фронталь
Профильная
7. Построить проекции отрезка АВ параллельного π1, длиной 40 мм и расположенного к плоскости π2 под углом 30°. Сколько решений имеет задача?
В2
x1 2
В1
8

Тема 2
Взаимное положение прямых (параллельные, пересекающиеся, скрещивающиеся, перпендикулярные). Комплексный чертеж плоскости. Плоскость общего положения, частного положения.
Прямая и точка в плоскости
Вопросы для самоподготовки
1.Как на чертеже располагаются проекции двух параллельных прямых, двух пересекающихся прямых?
2.В каком случае прямой угол проецируется в виде прямого угла?
3.Какие точки называются горизонтально- и фронтальноконкурирующими? Как определить их видимость на чертеже?
4.Как задается плоскость на чертеже?
5.Какие плоскости называются плоскостями общего положения, проецирующими, уровня? Как они изображаются на чертеже?
6.Каким свойством обладают проецирующие плоскости, плоскости
уровня?
7.Что такое след плоскости на плоскости проекций?
8.Что такое горизонталь, фронталь и линия ската плоскости?
9.Сформулируйте признак принадлежности точки плоскости, прямой плоскости.
8.Через точку А провести прямую а параллельную прямой b; пересекающую прямую с; скрещивающуюся с прямой d.
А2 |
|
b2 |
|
|
А2 |
|
c |
|
А2 |
|
d |
||||
|
|
|
|
|
2 |
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|||||||||
x |
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
b |
|
|
c1 |
|
|
|
d1 |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
А1 |
|
|
1 |
|
А1 |
|
|
|
А1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
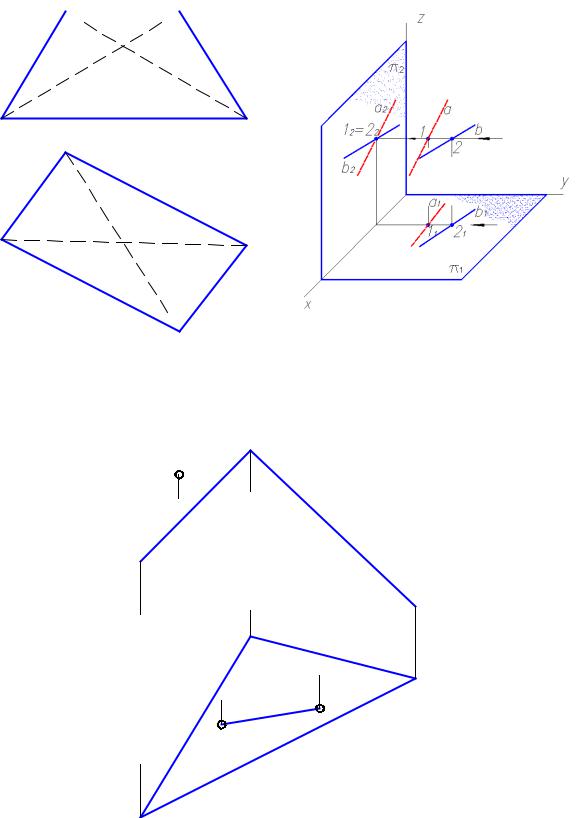
9. Определить видимость ребер многогранника. Доказать решение с помощью конкурирующих точек.
C2 
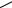 B2
B2
D2 |
A2 |
|
C1 |
D1 |
A1 |
 B1
B1
10. Построить недостающую проекцию точки Р и отрезка ЕF, лежащих в плоскости АВС.
C2
Р2
A2
 B2 C1
B2 C1
Е1 F1 B1
A1
10

11. Построить прямоугольник АВСD с вершиной С на прямой е.
|
|
е2 |
|
|
х1 2 |
|
В2 |
|
А2 |
|
|
|
|
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
е1 |
|
А1 |
|
|
|
||
|
|
|
||
|
|
|
|
11
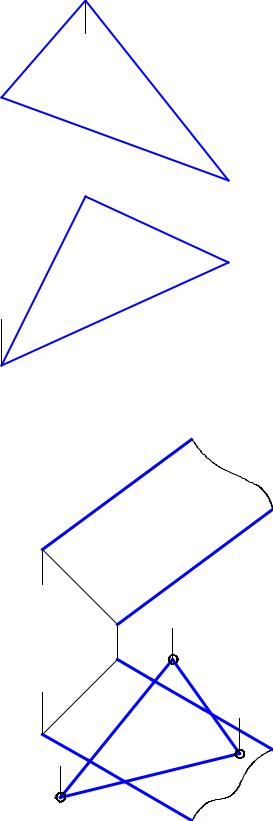
12. В плоскости, заданной треугольником АВС построить прямые: горизонталь h, А h; фронталь f; В f; линию ската u, С u.
C2
х1 2 |
A2 |
|
|
||
|
|||||
|
|
|
|
B2 |
|
|
|
|
|
||
|
|
|
|
||
|
|
C1 |
|
B1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
A1
13. Построить недостающую проекцию треугольника, расположен-
ного в плоскости (k // l ). |
k2 |
|
l2
C1
l1
A1 |
B1 |
|
k1 |
||
|
||
|
12 |

14. Построить фронтальную проекцию грани |
2 . Указать, |
какие |
|||
плоскости определяют грани многогранника. |
|
|
|
||
|
В2 =С2 |
|
|
|
|
5 |
|
|
Плоскость |
Грань |
|
|
|
|
|
|
|
|
4 |
3 |
Общего положения |
|
|
|
Горизонтально- |
|
|||
|
|
|
|||
|
А2 =D2 |
|
проецирующая |
|
|
|
|
Фронтально- |
|
||
|
А1 |
|
проецирующая |
|
|
|
|
Профильно- |
|
||
|
|
7 |
проецирующая |
|
|
|
6 |
Горизонтальная |
|
||
|
В1 |
|
уровня |
|
|
5 |
1 |
Фронтальная |
|
||
С1 |
уровня |
|
|
||
|
2 |
Профильная |
|
||
|
4 |
3 |
уровня |
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
15. Построить проекции прямой призмы длиной 60 мм. АВС – основание призмы. Определить видимость ребер призмы.
А2 
B2 
x1 2 |
С2 |
|
С1 |
||
|
А1
В1
13
Тема 3
Построения с простейшими геометрическими фигурами
Вопросы для самоподготовки
1.Сформулируйте аксиому принадлежности прямой и плоскости.
2.Каков признак параллельности двух плоскостей?
3.Сформулируйте признак параллельности прямой и плоскости.
4.Что такое горизонтально, фронтально и профильно проецирующие плоскости?
5.Назовите основное свойство проецирующих плоскостей.
6.Как установить взаимное положение прямой и плоскости?
________________________________________________________________
16. Построить недостающую проекцию треугольника, |
располо- |
женного в заданной плоскости. |
|
|
|
f 0 |
|
|
|
|
2 |
|
|
|
|
С2 |
|
|
|
|
В2 |
|
|
x1 2 |
А2 |
0 |
0 |
|
|
|
(f1 =h2 ) |
||
|
|
|||
h10
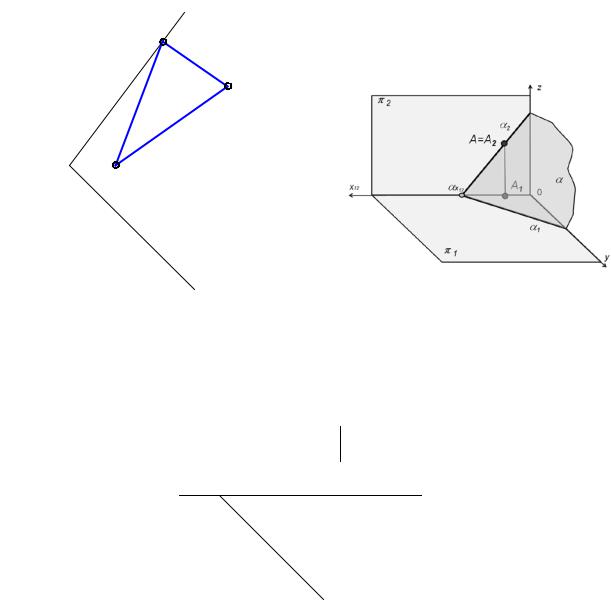
17. Построить фронтальный след f0 плоскости, заданной горизонтальным следом h0 и точкой А.







 А2
А2
x1 2







 А1
А1
h10
14

18. Построить проекции пятиугольника АВСDE.
А2
Е2
В2
С2 

С1 
 D1
D1
В1
А1
19. Через точку А провести прямую, пересекающую прямые b и с.
b2
A2 |
|
|
c2 |
|
|||
|
|
|
|
|
|
|
|
x1 2
c1
A1 b1
15

20. Достроить фронтальную проекцию ∆АВС, если его плоскость параллельна прямой d.
d2
A2 
 B2
B2
B1
A1 

C1 d1
21. Построить фронтальную проекцию прямого угла ВАС.
|
|
B2 |
x1 2 |
|
A2 |
|
B1 |
|
|
|
|
|
C1 |
|
|
|
A1 |
|
|
4 |
|
1 |
|
|
x |
|
|
|
16 |

22. Построить новую проекцию плоскости, чтобы она стала проеци-
рующей.
C2
B2
х1 2 |
A2 |
|
|
|
|
|
|
||
|
||||
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A1 |
|
|
|
|
|
|||
B1
17
