
1409
.pdf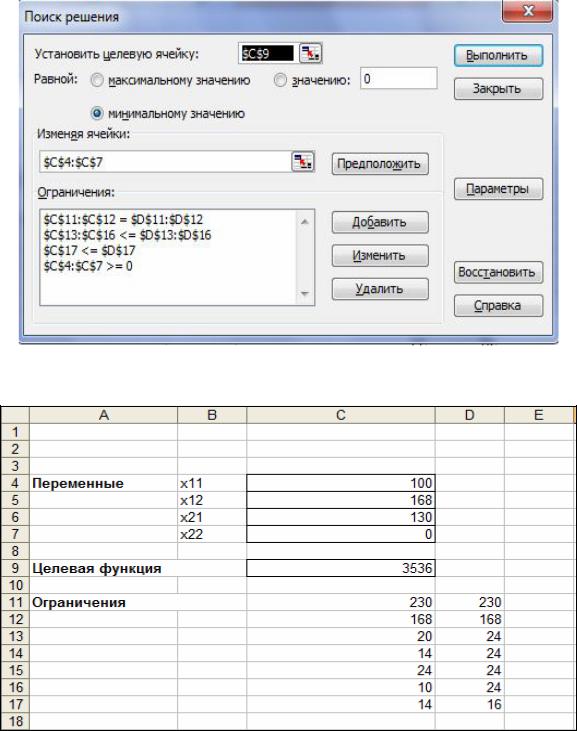
Рис. 4. Установка необходимых параметров задачи в окне Поиск решения
Рис. 5. Результат расчета надстройки Поиск решения
По результатам решения задачи можно сделать вывод, что для минимизации стоимости погрузочных работ первый погрузчик на первой площадке должен погрузить 100 т, на второй – 130 т, второй погрузчик на первой площадке – 130 т; использование второго
11
погрузчика на второй площадке в данных условиях нецелесообразно
(рис. 5).
Пример 2. Для работы в офисе автотранспортной компании требуется в понедельник - среду не менее 24 работников, в четверг и субботу – не менее 22 работников, в пятницу – не менее 20 работников, основной пик работы приходится на воскресенье, поэтому в воскресенье требуется не менее 28 сотрудников. Причем должен соблюдаться следующий рабочий график: каждый сотрудник работает 5 дней в неделю с двумя выходными подряд.
Дневная оплата сотрудников составляет 400 руб. (без учета премиальных и комиссионных).
Определите оптимальное количество человек в смену для обслуживания офиса автотранспортной компании с учетом минимума издержек на заработную плату, учитывая установленный график работы персонала [1].
Решение.
1. Математическая модель. Пусть xj – число сотрудников,
работающих по j-му графику. Матрица графиков работы сотрудников
А:
0 |
1 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
|||||
1 |
0 0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
|||||
1 |
1 |
1 |
1 0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 0 |
|
Матрица необходимого количества сотрудников на каждый рабочий день:
bТ 24 24 24 22 20 22 28 .
Матрица почасовой оплаты труда:
с 400 400 400 400 400 400 400 .
Система ограничений на обязательный минимум количества сотрудников в каждый рабочий день:
12
x2 x3 x4 x5 x6 24;x3 x4 x5 x6 x7 24;
x1 x4 x5 x6 x7 24;x1 x2 x5 x6 x7 22;
x1 x2 x3 x6 x7 20;x1 x2 x3 x4 x7 22;
x1 x2 x3 x4 x5 28.
Ограничение на неотрицательность переменных модели: xj >0.
Целевая функция – минимум затрат на заработную плату:
F400x1 400x2 400x3 400x4 400x5 400x6 400x7 min.
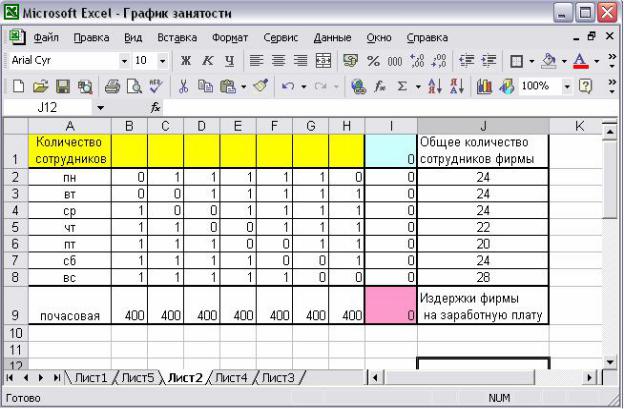
2.Ввод исходных данных. Экранная форма для ввода условий задачи вместе с введенными в нее исходными данными представлена на рис. 6.
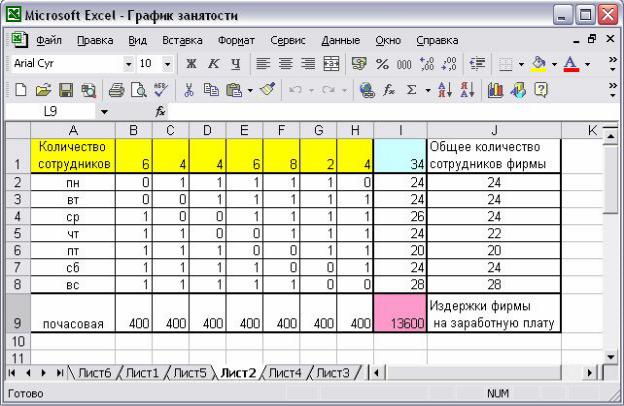
Рис. 6. Экранная форма задачи
При наборе графика работы персонала учитывается пять рабочих дней и два выходных в неделю. Все рабочие графики вводятся в
массив (B2:H8), причем «1» означает рабочий день графика, а «0» –
13
выходной. Так, первый график, представленный в столбце В, имеет два выходных (в понедельник и вторник) и 5 рабочих дней (со среды по воскресенье). Массив (B1:H1) соответствует переменным задачи, т.е. количеству сотрудников, работающих по определенному графику.
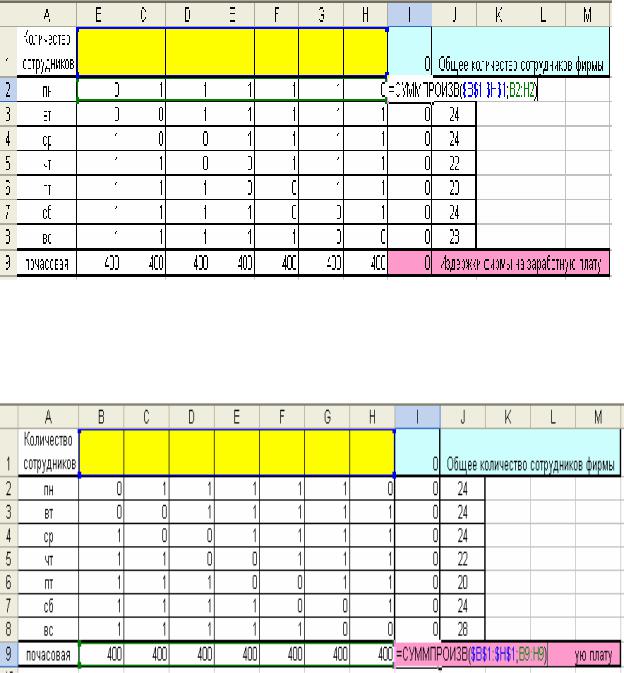
В ячейке I2 вводится формула СУММПРОИЗВ, рассчитывающая количество сотрудников, работающих в понедельник (рис.7). Аналогичные формулы вводятся и в ячейках I3:I8.
Рис. 7. Ввод левой части ограничений
В ячейке I9 вводится целевая функция издержек фирмы на заработную плату (рис. 8).
Рис. 8. Ввод целевой функции
14
Для расчета общего количества сотрудников вводится формула СУММ(В1:Н1) в ячейку I1.
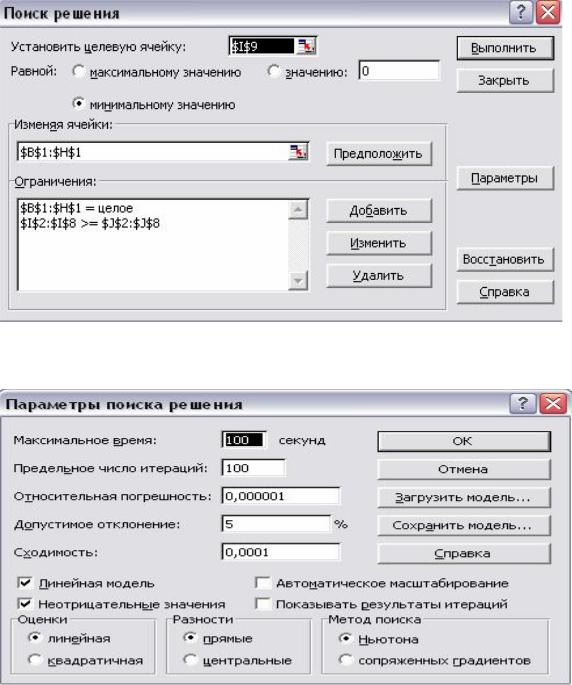
Граничные условия и ограничения вводят аналогично предшествующей задаче с помощью диалоговых окон Добавление ограничения и Параметры поиска решения. Целевую ячейку устремляют к минимуму. Окно Поиск решения после ввода всех необходимых данных задачи представлено на рис. 9.
Рис. 9. Окно Поиск решения задачи
Рис. 10. Окно Параметры поиска решения задачи
15
В данном примере можно использовать ограничение целых чисел, если дробное число сотрудников недопустимо. Можно
n
добавить ограничение на общее число сотрудников: xj Х , Х –
j 1
максимально допустимое число сотрудников фирмы. Выбор линейной модели и неотрицательных переменных в диалоговом окне Параметры ускорит получение результата (см. рис. 10). Решая данную задачу, получаем рис. 11:
Рис. 11. Экранная форма задачи после получения решения
Распределение сотрудников по рабочим графикам следующее:
6 сотрудников работают по рабочим графикам с выходными в понедельник-вторник и четверг-пятницу;
4 сотрудника работают по графикам с выходными вторниксреда, среда-четверг и воскресенье-понедельник;
8 сотрудников имеют график работы с выходными в пятницусубботу;
2 сотрудника – с выходными в субботу-воскресенье.
Всего фирме требуется 34 сотрудника, еженедельные затраты на
16
заработную плату – 13600 руб.
Задачи для самостоятельной работы [1]:
1. Необходимо составить оптимальный график работы служащих фирмы, занимающейся грузоперевозками, с учетом минимума издержек на заработную плату, учитывая установленный график работы персонала. Известно, что в офисе фирмы требуется в понедельник - четверг не менее 8 работников, в пятницу и субботу – не менее 10 работников, в воскресенье – не менее 12 работников. Причем должен соблюдаться следующий рабочий график: каждый сотрудник работает 6 дней в неделю с одним выходным.
Дневная оплата сотрудников составляет 650 руб. для графиков работы с выходными в субботу или воскресенье и 600 руб. – с выходными в другие дни (без учета премиальных и комиссионных). Изменится ли график работы персонала, если дневная оплата для всех сотрудников будет 600 руб.?
2.Для обслуживания парка компьютеров в автотранспортном предприятии требуется не менее пяти человек в день: 4 оператора ЭВМ, администратор. Нагрузка на использование компьютеров возрастает со среды по пятницу, причем нагрузка распределяется таким образом, что основной пик приходится на четверг. Поэтому в эти дни требуются дополнительные человекоресурсы – по 1 сотруднику в среду и пятницу и 2 сотрудника в четверг. Таким образом, получается, что максимальное количество работников в смену составляет 7 человек. Причем должен соблюдаться следующий рабочий график: каждый сотрудник работает 5 дней в неделю с двумя выходными подряд. Дневная оплата сотрудников составляет 750 руб. (без учета премиальных и комиссионных). Рассчитайте минимальную недельную заработную плату сотрудников. Определите оптимальное количество человек в смену для обслуживания парка компьютеров с учетом минимума издержек на заработную плату, учитывая установленный график работы персонала.
3.Для обслуживания клиентов и организации работы в крупном автотранспортном предприятии требуется не менее 100 человек в день. Нагрузка на использование оборудования снижается с пятницы по воскресенье, т.е. в выходные дни, причем нагрузка распределяется таким образом, что основной спад приходится на воскресенье. Поэтому в выходные дни количество работающих уменьшается – по 15 сотрудников в пятницу и субботу и 20 сотрудников в воскресенье. При составлении расписания должен соблюдаться следующий
17
рабочий график: каждый сотрудник работает 5 дней в неделю с двумя выходными подряд. Дневная оплата сотрудников составляет 550 руб. Рассчитайте минимальную недельную заработную плату сотрудников. Определите оптимальное количество человек в смену для обслуживания клиентов предприятия с учетом минимума издержек на заработную плату, учитывая установленный график работы персонала.
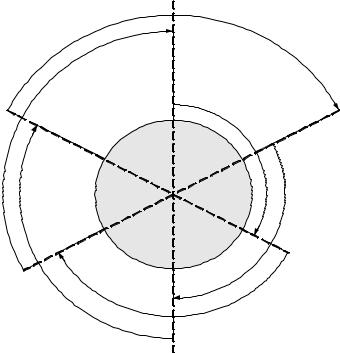
4. Управление городским автобусным парком решило провести исследование возможности более рациональной организации своей работы с целью снижения интенсивности внутригородского движения. Сбор и обработка необходимой информации позволили сделать вывод, что необходимое минимальное количество автобусов существенно меняется в течение суток (рис.12). Длительность непрерывного использования автобусов на линии равна 8 ч в сутки (с учетом необходимых затрат времени на текущий ремонт и обслуживание). График перекрывающихся смен представлен на рис.13.
Количество автобусов
12 |
|
|
12 |
|
|
|||
|
|
10 |
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
8 |
|
|
|
|
|
8 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
4 |
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00:00 |
4:00 |
8:00 |
12:00 |
16:00 |
20:00 |
00:00 |
Часы суток
Рис.12. Минимально необходимое количество автобусов на линии
18
00:00
20:00 4:00
16:00 8:00
Полдень
12:00
Рис.13. График перекрывающихся смен
Постройте математическую модель, позволяющую узнать, какое количество автобусов необходимо выпускать на линию в каждой из смен при условии, что общее количество автобусов, выходящих на линию в течение суток, должно быть минимальным.
2.2. Пример решения транспортной задачи с использованием автоматизированных систем управления
Формулировка транспортной задачи линейного программирования представленав научныхисточниках [2]. В данных методических указаниях рассмотрен пример решения транспортной задачи с использованием автоматизированных систем управления [4].
Производство продукции осуществляется на четырех предприятиях, а затем развозится в 5 пунктов потребления. Предприятия могут выпускать в день 235, 175, 185 и 175 единиц продукции. Пункты потребления готовы принимать ежедневно 125, 160, 60, 250 и 175 единиц продукции. Хранение на предприятии единицы продукции обходится в 2 у. е. в день, штраф за недопоставленную продукцию – 3,5 у. е. в день. Стоимость перевозки единицы продукции (в у. е.) с предприятий в пункты потребления приведена в табл. 4.
19
|
|
Транспортные расходы |
|
Таблица 4 |
|||
|
|
|
|
||||
|
|
|
|
|
|
|
|
Предприятия |
|
|
Пункты потребления |
|
|
||
1 |
2 |
|
3 |
|
4 |
5 |
|
|
|
|
|||||
1 |
3,2 |
3 |
|
2,35 |
|
4 |
3,65 |
2 |
3,0 |
2,85 |
|
2,5 |
|
3,9 |
3,55 |
3 |
3,75 |
2,5 |
|
2,4 |
|
3,5 |
3,4 |
4 |
4 |
2 |
|
2,1 |
|
4,1 |
3,4 |
Решение задачи сводится к реализации следующих этапов [4]:
1.Проверка сбалансированности модели задачи. Модель является сбалансированной, т. к. суммарный объем производимой продукции в день равен суммарному объему потребности в ней:
235 + 175 + 185 + 175 = 125 + 160 + 60 + 250 + 175.
2.Построение математической модели. Неизвестными в этой задаче являются объемы перевозок. Пусть xij – объем перевозок с i-го предприятия в j-й пункт потребления; ai – объем производства на i-м предприятии; bj – спрос в j-м пункте потребления; cij – стоимость перевозки единицы продукции с i-го предприятия в j-й пункт потребления. Суммарные транспортные расходы – это функционал качества (критерий цели):
n m
Fcij xij .
i1 j 1
Неизвестные в этой задаче должны удовлетворять следующим ограничениям: объемы перевозок не могут быть отрицательными; поскольку модель сбалансирована, то вся продукция должна быть вывезена с предприятий, а потребности всех пунктов потребления должны быть полностью удовлетворены. Найти минимум
4 5
функционала F cijxij min приограничениях
i 1 j 1
5
xij ai ,i 1,4;
j1 4
xij bj , j 1,5;
i 1
xij 0,i 1,4 , j 1,5.
20
