
1369
.pdf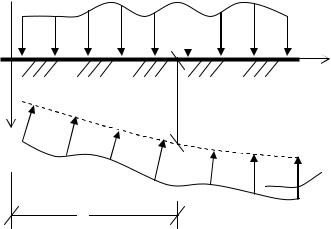
В.Н. Завьялов, В.М. Романовский, Е.Я. Гайнулин
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Часть II
Учебное пособие
 q(z)
q(z)
|
z |
y |
(z) |
|
r(z) |
z
11
Федеральное агентство по образованию Сибирская государственная автомобильно-дорожная академия (СибАДИ)
В.Н. Завьялов, В.М. Романовский, Е.Я. Гайнулин
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Часть II
Учебное пособие
Омск Издательство СибАДИ
2008
12
УДК 624.01 ББК 30.121 С 64
Рецензенты:
д-р техн. наук, проф. О.В. Матвиенко (ТГАСУ); канд. техн. наук О.Н. Попов (ТГАСУ)
Работа одобрена редакционно-издательским советом академии в качестве учебного пособия для студентов строительных специальностей.
С 64 Сопротивление материалов. Ч. II: Учебное пособие / В.Н. Завьялов, В.М. Романовский, Е.Я. Гайнулин. – Омск: Изд-во СибАДИ, 2008. – 80 с.
ISBN 978 5 93204 344 8
В настоящем учебном пособии изложены темы, изучаемые студентами очной формы обучения в четвёртом семестре, соответствующие в основном рабочим программам для строительных специальностей. Отдельные темы учебного пособия могут быть использованы студентами, обучающимися на других специальностях.
Ил. 59. Табл. 2. Библиогр.: 10 назв.
ISBN 978 5 93204 344 8 |
В.Н. Завьялов, В.М. Романовский, |
|
Е.Я. Гайнулин, 2008 |
13
В.Н. Завьялов, В.М. Романовский, Е.Я. Гайнулин
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Часть II
Учебное пособие
Омск 2008
14
ПРЕДИСЛОВИЕ
Настоящее учебное пособие является продолжением ранее написанного курса лекций «Механика деформируемого твёрдого тела» (Ч. I. Сопротивление материалов), изданного издательством СибАДИ в 2001 году. Представленное вниманию читателей учебное пособие включает в себя темы, соответствующие действующим в настоящее время рабочим программам по сопротивлению материалов для строительных специальностей. Некоторые темы, такие, например, как устойчивость однопролётных сжатых стержней, расчеты на удар и другие, могут быть использованы и студентами, обучающимися на механических специальностях.
Открывает настоящее учебное пособие раздел, в котором рассматриваются основные положения классических теорий прочности, освоение которых позволяет выполнять расчеты элементов конструкций с пониманием физической сути работы таких элементов.
Во втором разделе представлены основные теоретические обоснования расчета балок, лежащих на сплошном упругом основании. Освоение этого материала студентами строительных специальностей особенно важно, так как в практике как транспортного строительства, так и строительства других сооружений очень часто встречаются конструкции, в основании которых находится упругая среда.
Сложное сопротивление, являющееся в инженерной практике самым распространенным видом деформирования элементов конструкций, представлено в третьей главе.
Устойчивость однопролетных сжатых стержней, имеющих различные типы краевых закреплений, рассмотрена в четвертом разделе настоящего учебного пособия.
Впятом разделе рассмотрены принципиальные положения расчета балок на действие такого вида динамической нагрузки, каким является удар.
Весьма важным в глубоком осмыслении прочностных расчетов элементов конструкций является знание и понимание основных уравнений теории упругости, представленных в шестом разделе пособия.
Взаключительном разделе учебного пособия даны начальные сведения
орасчете тонкостенных элементов конструкций, испытывающих как свободное, так и стеснённое кручение.
15
1. ТЕОРИИ ПРОЧНОСТИ
1.1. Основные положения
Важнейшей задачей сопротивления материалов является расчёт конструкций на прочность и жесткость. Чтобы оценить опасное состояние элемента конструкции, необходимо уметь определять предельное по прочности (жесткости) напряжение (перемещение) в любом сложном напряженном состоянии элемента конструкции. Наиболее просто можно оценить напряженное состояние элемента конструкции при одноосном действии на него внешней нагрузки, что соответствует наиболее простому виду деформирования элемента – растяжению-сжатию. В этом случае напря- жённо-деформированное состояние элемента конструкции определится всего одним главным напряжением, вектор которого направлен вдоль оси элемента перпендикулярно его поперечному сечению.
При плоском напряженном состоянии предельное напряженное состояние будет уже определяться величинами и соотношениями двух главных напряжений, а при объемном – тремя.
При этом для пластичного материала за предельное принимается такое состояние, при котором появляются значительные остаточные пластические деформации, т.е. σ = σy, а для хрупких – начало разрушения (σ = σu). Если известна расчетная величина напряжения R, то коэффициент запаса определяют как n = R/σ.
Для того чтобы эффективно оценить напряженное состояние конструкции, необходимо опытным путем определить значения всех главных напряжений и их соотношения. Однако в настоящее время, несмотря на достаточно высокий уровень эксперимента, такое не представляется возможным. Вместе с тем инженерная практика и экспериментальные исследования в лабораториях позволили накопить прекрасную базу статистических данных напряженно-деформированного состояния элементов конструкций, испытывающих вид деформирования, называемый растяжениесжатие. Поэтому именно этот вид деформирования элемента конструкции принимают как бы за эталон прочности и ставят условия равнопрочности (т.е. соответствия) для эталона любого сложного напряженного состояния. Установлением такого соответствия и занимаются теории прочности, которых уже насчитывается несколько десятков.
Построение теорий прочности основывается на предпосылке, состоящей в том, что два каких-либо напряженных состояния считаются равнопрочными и равноопасными, если они при пропорциональном увеличении главных напряжений одновременно становятся предельными.
Общий ход решения задачи построения той или иной теории прочности на основе сказанного будет следующим:
16
1.Вводят определенную меру прочности в виде прочности при одноосном напряженном состоянии.
2.Выдвигают по данной теории прочности решающий фактор или критерий прочности (напряжение, либо деформация, либо энергия деформации и др.).
3.Устанавливают характеристики прочности для элемента тела в сложном напряженном состоянии и отдельно для эталона.
4.Составляя условия равнопрочности (т.е. соответствия) сложного напряженного состояния эталону, получают расчетное уравнение прочности.
5.Проверяют полученное расчетное условие на опытном материале.
1.2. Классические теории прочности
Теория наибольших нормальных напряжений, когда принимают, что причиной наступления предельного состояния является наибольшее нормальное напряжение. При этом главные напряжения находятся в зависимости
1 2 3. |
(1.1) |
В соответствии с принятой гипотезой, действительно, |
|
max 1 0, |
(1.2) |
где 1 – величина наибольшего из главных напряжений для исследуемого напряженного состояния; 0 – предельное напряжение, полученное из опыта для одноосного действия нагрузки.
По методу предельных состояний это условие запишется как
max 1 0 R, |
(1.3) |
где R – расчетное сопротивление.
Недостатком этой теории прочности является то, что не учитывается влияние двух других главных напряжений.
Теория наибольших продольных деформаций, когда принимают, что предельное состояние наступает тогда, когда наибольшее относительное удлинение max в сложном напряженном состоянии достигает величины, опасной для материала, т.е.
max 1 0 . |
(1.4) |
где 1 – наибольшее расчетное удлинение для исследуемого напряженного состояния; 0 – для эталона.
Для объемного напряженного состояния в соответствии с законом Гука
17
1 |
1 v( 2 3) |
. |
|
(1.5) |
||||||
|
|
|
|
|
||||||
Для эталона |
Е |
|
||||||||
|
0 |
|
|
|
|
|
|
|||
|
|
0 |
. |
|
|
|
(1.6) |
|||
|
|
|
||||||||
|
|
|
|
Е |
|
|||||
Тогда на основании (1.4) |
|
|
|
|
|
|
|
|
||
|
1 v( 2 3) |
|
0 |
. |
(1.7) |
|||||
|
|
|||||||||
|
|
E |
|
|
|
|
E |
|
||
По методу предельных состояний, (1.7) принимает вид |
|
|||||||||
|
1 v( 2 |
|
3) R. |
(1.8) |
||||||
Недостатком этой теории прочности является то, что, как показывает опыт, эта теория подтверждается только для хрупких материалов.
Теория наибольших касательных напряжений предполагает, что пре-
дельное состояние по прочности наступает тогда, когда наибольшее напряжение для элемента тела в сложном напряженном состоянии достигает величины касательного напряжения для эталона, т.е.
max 0. |
(1.9) |
||
Для объемного напряженного состояния |
|
||
max |
1 3 |
. |
(1.10) |
|
|||
2 |
|
|
|
Для одноосного действия нагрузки
0 |
|
0 |
. |
(1.11) |
|
||||
|
2 |
|
|
|
В соответствии с изложенным, действительно,
1 3 0. |
(1.12) |
Для предельного состояния (1.12) принимает вид |
|
расч 1 3 R. |
(1.13) |
Недостатком этой теории прочности является то, что в случае объемного напряженного состояния не учитывается главное напряжение 2 .
Теория предельного значения энергии формообразования (теория Губера-Мизеса) предполагает, что в предельном состоянии следует вводить энергию, идущую на изменение формы элемента, что соответствует выражению
Uф Uф0 . |
(1.14) |
18 |
|
Энергия, идущая на изменение формы элемента конструкции, описывается через главные напряжения:
Uф |
|
1 v |
1 |
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
(( 1 |
|
2) |
|
( |
2 |
3) |
|
( |
3 1) |
|
) . |
(1.15) |
|
3E |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для эталона эта энергия описывается выражением
|
|
|
|
1 v |
2 |
|
|
|
||
|
|
|
Uф0 |
|
1 . |
|
|
(1.16) |
||
|
|
3E |
|
|
||||||
|
|
|
|
|
|
|
|
|
||
Тогда справедливо записать |
|
|
|
|
|
|
||||
( 1 2)2 ( 2 |
3)2 ( 3 |
1)2 2 12. |
(1.17) |
|||||||
По методу предельных состояний, (1.17) имеет вид |
|
|||||||||
|
|
|
|
|
|
|
|
|||
расч |
1 |
( 1 2)2 |
( 2 3)2 |
( 3 1)2 R. |
(1.18) |
|||||
2 |
||||||||||
|
|
|
|
|
|
|
|
|
||
Изложенная теория прочности достаточно хорошо соответствует упругопластическим материалам.
Теория Мора. Теория прочности Мора пренебрегает влиянием на общее напряженное состояние главного напряжения 2 , ко-
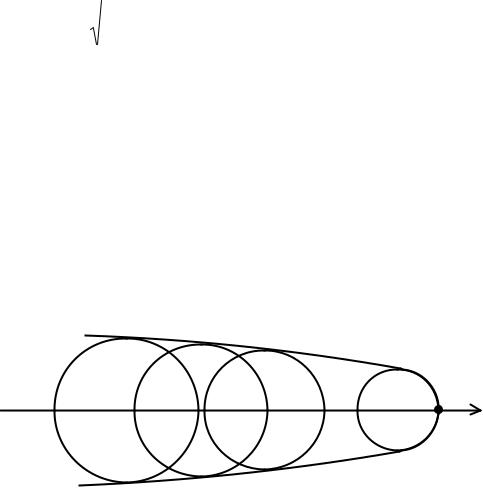
торое составляет 10 15% от всего напряжённого состояния элемента конструкции. Если для каждого материала имеются данные об его опасных состояниях при различных соотношениях между главными напряжениями, то можно построить (рис. 1.1) семейство кругов Мора.
Круг Мора превращается в точку, когда 1 = 2 = 3.

Рис. 1.1
19
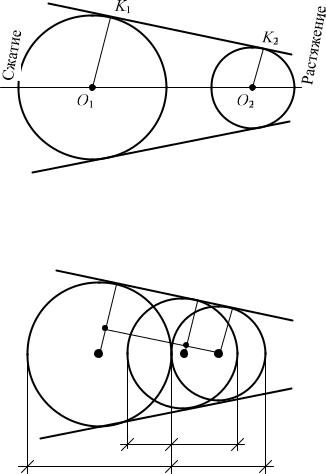
Огибающая этих кругов будет характеризовать безопасную область работы материала. Точка C характеризует случай всестороннего равномерного растяжения. Левее этой точки всё большим становится равномерное сжатие, а незамкнутость огибающей говорит о том, что при всестороннем сжатии материал практически не разрушается.
Однако такое семейство кругов Мора из опыта пока получить невозможно. Поэтому построим только два круга Мора, легко получаемых из опыта на растяжение-сжатие. При этом кривую, огибающей круги Мора (рис. 1.2), заменяют прямыми линиями. Эти прямые являются границами области предельных напряжений и устанавливают одновременно прямо пропорциональную зависимость между главными напряжениями σ1 и σ3 всякого напряженного состояния, главный круг которого касается этих прямых, т.е. 1 a b 3.
Рис. 1.2
Внесем круг в такую диаграмму.
|
|
С1 |
|
е |
|
С3 |
С2 |
и |
B1 |
|
|
т |
|
|
|
а |
|
B3B2 |
|
ж |
|
||
С |
|
|
|
|
О1 |
О3 |
О2 |
3 1
ос ор
е и н е яж т с а Р
Рис. 1.3
На рис. 1.3 ос – предельное напряжение при сжатии; ор – предель-
ное напряжение при растяжении.
Рассмотрим подобие треугольников О1В1В2 и О3В3В2:
20
