

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2 Сокращение срока строительства делением захватки
на составляющие части (подзахватки)
Задача 1. Рассчитать продолжительность работ без деления на подзахватки. Рассчитать матрицу, разделив захватки на подзахватки. Определить сокращение срока строительства объекта.
|
процесс |
|
подз- |
|
|
|
|
|
|
|
|
|
|
захватка |
|
ки |
|
1 |
|
|
2 |
|
3 |
|
|
и |
0 |
|
|
5 |
|
|
7 |
|
|
|||
СI |
|
а |
|
3 |
3 |
|
2 |
7 |
5 |
|
|
|
|
|
|
|
|
|
|
12 |
|
||||
|
|
3 |
2 |
|
7 |
2 |
|
12 |
|
|
||
|
|
|
|
|
5 |
|
9 |
4 |
16 |
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
5 |
|
|
9 |
|
|
16 |
|
|
б |
|
4 |
|
3 |
|
|
||||||
|
|
|
а |
|
4 |
9 |
|
13 |
19 |
|
||
|
II |
|
|
9 |
|
|
13 |
|
|
19 |
|
|
|
|
|
|
|
3 |
12 |
|
5 |
18 |
4 |
23 |
|
|
|
|
|
12 |
|
|
18 |
|
|
23 |
|
|
|
|
А |
2 |
|
|
|||||||
|
|
|
а |
|
2 |
14 |
|
3 |
21 |
25 |
|
|
|
III |
|
|
14 |
|
21 |
|
|
25 |
|
|
|
|
|
|
|
|
2 |
16 |
|
2 |
23 |
3 |
28 |
|
|
|
|
|
16 |
|
23 |
|
|
28 |
|
|
|
|
|
|
а |
|
4 |
20 |
|
4 |
27 |
2 |
30 |
|
|
IV |
|
|
|
|
|
|
|
|
|||
|
|
|
20 |
|
27 |
|
|
30 |
|
|
||
|
|
|
б |
|
5 |
25 |
|
3 |
30 |
2 |
32 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис. 4. Матрица сокращения срока строительства |
|||||||||||
|
|
|
|
|
|
|
|
|
И |
|||
Варианты заданий для практическогоДзанятия № 2 взять по приложению 3.
2. СЕТЕВОЕ МОДЕЛИРОВАНИЕ
Общие положения
В основе метода сетевого планирования и управления (СПУ) лежит построение графика, по своему виду напоминающего сеть (переплетение нитей и узелков). Поэтому и график получил название сетевого.
Сетевой моделью называется отображение процессов, выполнение которых подчинено достижению одной или нескольких целей, с указанием взаимосвязей между этими процессами.
7
Сетевым графиком называется график производства работ с установленными расчётом сроками их выполнения. Сетевой график представляет собой графическое изображение сетевой модели с рассчитанными параметрами.
Элементами сетевой модели являются «работа», «событие» и «путь». Работа – это трудовой процесс, требующий затрат времени и ресурсов. Название работы является минимальной информацией о работе,
содержащейся в сетевой модели (например, «отрывка котлована», |
|||||
возведение каркаса, устройство кровли, поставка оборудования и т.д.) |
|||||
ли |
|
|
направленной |
||
Работа на граф ке |
зображается сплошной стрелкой, |
||||
Сслева направо с указан ем над стрелкой продолжительности работы. |
|||||
Работа, которая тре ует лишь затрат времени, называется «работа – |
|||||
ожидан е». «Ож дан |
» на графике изображается пунктирной стрелкой, с |
||||
|
бетона |
|
|
||
указан ем над стрелкой её продолжительности (например, процесс |
|||||
тверден я |
|
ожидания |
поставки |
материалов) |
Эти работы |
требуют только затрат времени . |
|
|
|
||
|
А |
|
|||
Для отображен я правильной технологической очерёдности между |
|||||
работами применяется |
- «зависимость» |
Ни времени, |
ни ресурсов |
||
«зависимость» не тре ует. На |
графике |
«зависимость» |
изображают |
||
пунктирной стрелкой, продолжительность которой равна нулю. Итак,
понятие «работа» может иметь три значения: работа, работа-ожидание, |
|
зависимость. |
Д |
|
|
Событие – это итог какой-нибудь деятельности (работы). Любая работа начинается и заканчивается событием.
Событие не потребляет ни времени, ни трудовых ресурсов, оно обозначает только факт начала и окончания однойИили нескольких работ. Событие графически обозначается кружком, внутри которого ставится его номер, или может обозначаться буквами.
Событие, не имеющее непосредственно предшествующих работ, называется исходным, не имеющим непосредственно следующих работ – завершающим. Событие, не являющееся ни исходным, ни завершающим,
называется промежуточным.
8
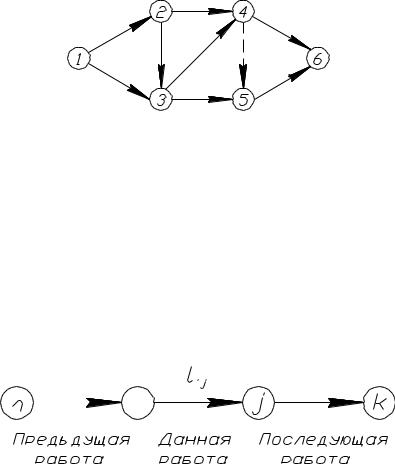
Рис. 5. События, работы, зависимость
На р сунке 5 событ е «1» – исходное, событие «6» – завершающее,
«2,3,4,5» – промежуточные. |
|
СВсе работы комплекса по отношению друг к другу подразделяются на |
|
«данную работу», «предшествующую» и «последующую работы». |
|
Обозначен е |
представлено на рисунке 6. |
события |
|
работ |
|
|
А |
|
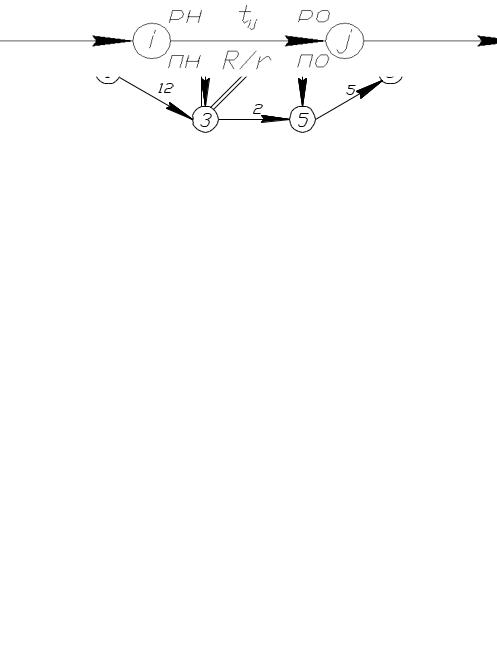
Рис. 6. Обозначение работ |
Путь – это непрерывная технологическаяДпоследовательность работ от исходного события к завершающему.
На рисунке 7 дан сетевой график из 8-ми работ, одной зависимости и из шести событий. На графике можно выделить 5 путей:
1-й путь проходит по событиям 1,2,3,4,6; |
И |
|
2-й путь проходит по событиям 1,3,5,6; |
||
3-й путь проходит по событиям 1,2,4,6; |
||
4-й путь проходит по событиям 1,2,3,5,6; |
||
|
5-й путь проходит по событиям 1,2,3,4,5,6;
6-й путь проходит по событиям 1,2,4,5,6.
7-й путь проходит по событиям 1,3,4,5,6
Зная продолжительность каждой работы tij, можно определить
9
продолжительность любого пути сетевого графика. |
|
|
|||||
Продолжительность |
пути |
(Т) |
|
определяется |
как |
сумма |
|
продолжительностей работ, составляющих этот путь: |
|
|
|||||
С |
T= tij |
|
|
( 1 ) |
|
|
|
Критический путь – это путь, имеющий максимальную |
|||||||
продолжительность. Он определяет конечный срок строительства, это |
|||||||
самый трудоемк й неблагоприятный путь. |
|
|
|||||
и |
|
|
|
|
|
||
б |
|
|
|
||||
|
|
Рис. 7. Сетевой график |
|
|
|||
|
А |
|
|
||||
На рисунке 7 длина критического пути |
|
(Ткр) от исходного события до |
|||||
завершающего равна |
Т1-2+ Т2-3+ |
Т3-4+ |
Т4-6. Критический |
путь |
показан |
||
двойными линиями.
Т = 5+10+14+9 = 38 дней
Правила построения сетевых моделейДи дополнительный теоретический материал изучить по [1,2], по лекции, либо по ссылке https://cloud.mail.ru/public/DyQ5/f2GP4PQaU, либо получить у преподавателя раздаточный материал к практическому занятию.
Алгоритм расчета сетевого графика (СГ) секторным методом. Параметры СГ. Пример расчета СГ
При расчёте сетевого графика определяются следующие временные параметры, представленные на рисунке 8 .
ПРАКТИЧЕСКОЕ ЗАНЯТИЕИ№ 3
Рис. 8 . Параметры сетевого графика
10
РН – ранее начало работы, самый ранний из возможных сроков начала работ, который обуславливается выполнением всех предшествующих работ.
РО – раннее окончание работы, самый ранний из возможный сроков Сокончания работы.
ПН – позднее начало работы, самый поздний срок начала работы, при котором план руемый срок достижения конечной цели не меняется.
ПО – позднее окончание работы, самый поздний допустимый срок целиокончан я работы, при котором планируемый срок достижения конечной
не меняется.
R – полный (о щ й) резерв времени показывает, насколько можно увелич ть продолж тельность ра оты или отодвинуть её начало, не изменяя конечныйработсрок строительства.
r – (свободный) частный резерв времени показывает на сколько можно увелич ть продолж тельность ра оты или отодвинуть её начало, не
1.Определяем ранниеАсроки начала и окончания работ РН и РО, рассматривая график слева на право.
Ранний срок наступления исходногоДсобытия равен нулю.
Т1РН = 0.
ТijРО = ТijРН + tij – раннее окончание работы ij равно сумме раннего
начала работы i-j и её продолжительности.
ТijРН = max ТijРО – раннее начало данной работыИравно наибольшему значению из ранних окончаний предшествующих работ.
2.Ранний срок наступления последнего события считаем и поздним сроком окончания работ.изменяя
рассматривая график справа налево.
ТijПН = ТijПО – tij – позднее начало работы i-j равно разности позднего окончания работы ij и её продолжительности tij.
ТijПО = max TijПН – позднее окончание данной работы равно наименьшему из поздних начал последующих работ.
11
4. |
Определяем работы, лежащие на критическом пути. Критический путь |
|
|
проходит по работам, у которых: |
|
|
ТijПО = ТijРО – сроки наступления раннего и позднего окончания работы |
|
|
равны, или |
|
|
ТijПН = ТijРН – сроки наступления позднего и раннего начала одинаковы. |
|
С |
|
|
5. |
Определяем резервы времени работ: |
|
|
Общий резерв Rij = TПОij – TPHij |
- tij; |
|
Частный резерв времени работы: |
|
|
rij = TРНjk – TРНij – tij, равен разности раннего начала |
|
|
последующ х работ раннего окончания данной работы. |
|
|
Секторный способ расчета сетевого графика[2]. |
|
|
работе |
|
|
Чтобы не загромождать сетевой график большим количеством |
|
временныхипараметров (на одной |
их показывается 7 – РН, РО, t, |
|
ПН, ПО, R, r) все нео ходимые расчёты данные о работах и событиях |
||
|
А |
|
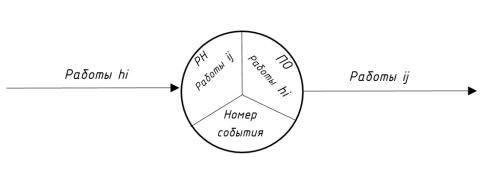
графика даются внутри со ытия. Каждое событие делится на 3 сектора, в |
||
которых показываются параметры. |
|
|
|
|
Д |
|
|
И |
|
Рис. 9. Деление события на секторы |
|
Разберем расчет СГ секторным способом, выполненный на рисунке 10.
12
