Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

645

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

613.25 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 33

						q r2															C
Отсюда,		D										3											1	1												M						0		.		Следовательно,
Отсюда,		D										3												1												M								.		Следовательно,
			Т			16D																2
						16D																2
					C						q r2 3													-					2M						0						.
																																			0
											8D							1									D				1
						1					8D							1									D				1
														Т														Т
Окончательно, уравнение угла поворота срединной поверхности
							q,M																r							q r								2
днища примет вид:																																								M								.
днища примет вид:																				D		1										8								M								.
						Т								0						D		1										8															0
																				Т
Радиальный погонный изгибающий момент
					M		rT								q					3 r2 r2 M																											,
					M															3 r2 r2 M																											,
												16D																				0													0
																	Т
где r0 – текущий радиус пластины (днища).																																													пластины малы,
Считают,		что				радиальные																перемещения																							пластины малы,
wТ Q0 wТ M0 0,							взаимное радиальное перемещение пластины
и оболочки w						w											w																		q r2
																																											1								. С учетом
																																				E h							1							2	. С учетом
		Ц		Q0							Т M					0										Ц		q								E h														2
(27) радиальное перемещение оболочки																												q r2
							Q													M		0						q r2
									0													0															1										.				(а)
						2			3 D																			E				h					1							2			.				(а)
						2			3 D								2 2 D											E				h												2
Остается сравнить взаимные угловые перемещения днища и
цилиндрической оболочки																					q r3
			Q								M		0								q r3																M				0		r
				0									0																												0								.		(б)
		2 2 D								D									8D				1											D					1										.		(б)
																					Т																Т
Совместное решение (а) и (б) дает
								Q0 M0																	q
																												1											;
																								2				1								2			;
																								2												2

						q r2 D																	r										1
																																	1									2
	M																																									2								.

			0			1								r			8D 1																				E h
			0			1								r			8D 1																				E h


						2					1
						2					1

1. Уравнение прогибов цилиндрической оболочки

e x

w x 2D 3 M0 sin x cos x Q0 cos x ; 2. Угол поворота срединной поверхности

e x cos x Q e x sin x cos x ;

2D 3

Погонный изгибающий радиальный момент

d2w

e x sin x cos x Q e x

sin x ;

dx2

Погонная поперечная сила

Q x

d3w

2 M

e x sin x Q e x cos x sin x .

dx3

6Mr

Радиальное напряжение

сравнить с допускаемым

и, в случае необходимости, откорректировать h.

Библиографический список

1.Бояршинов С.В. Основы строительной механики машин. Уч. пособие для студентов вузов.– М.: Машиностроение, 1973.

2.Доннелл Л.Г. Балки, пластини и оболочки: Пер. с англ./ Под ред. Э.И. Григолюка. – М.: Наука, 1982.

3.Искрицкий Д.Е. Строительная механика элементов машин.– Л.: Судостроение, 1969.

4.Макаров Е.Г. Инженерные расчеты в Mathcad. Уч. курс. – СПб.: Питер, 2005.

5.Макаров Е.Г. Сопротивление материалов на базе Mathcad. – СПб.: БХВ

– Петербург, 2004.

6.Папкович П.Ф. Тр. по строительной механике корабля в 4-х томах. Т. 3. Сложный изгиб стержней и изгиб пластин./ Под общ. ред. В.В. Екимова.– Л. Судостроение, 1962.

7.Погорелов В.И. Строительная механика тонкостенных конструкций. – СПб.: БХВ – Петербург, 2007.

8.Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки: Пер. с англ. – М.: Наука, 1966.

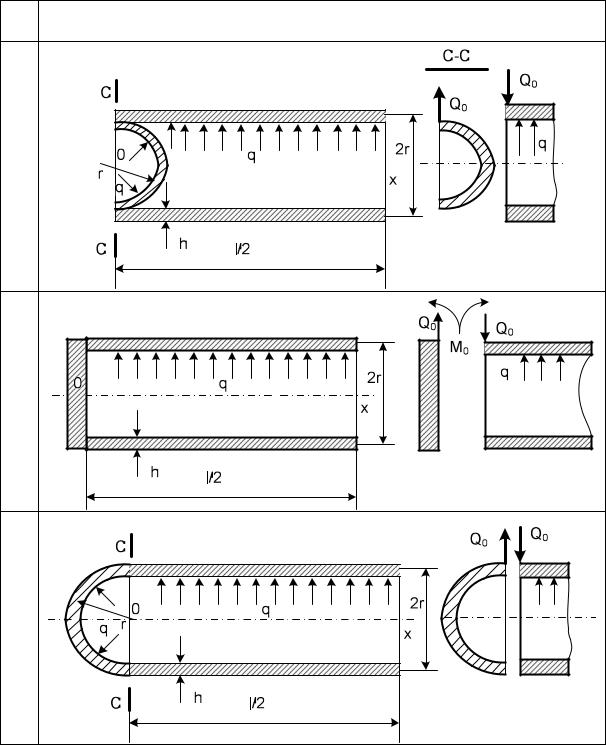
	Расчетные схемы оболочек
	Таблица 1
№	Схема
п/п
1
2
3

Исходные данные

						Таблица 2
№			Исходные данные
№
вар.	Схема	q кН/м2	h м	l м	r	E ГПа

1	2	40	0,004	0,25	0,06	210
2	3	35	0,005	0,28	0,055	210
3	5	30	0,003	0,26	0,075	200
4	2	25	0,0025	0,24	0,08	200
5	4	40	0,006	0,22	0,065	210
6	4	30	0,0045	0,23	0,07	200
7	2	32	0,003	0,20	0,08	200
8	3	36	0,004	0,22	0,085	210
9	5	44	0,006	0,26	0,065	210
10	2	46	0,009	0,28	0,065	200
11	4	44	0,008	0,28	0,08	200
12	5	20	0,003	0,22	0,055	210
13	2	25	0,003	0,23	0,09	210
14	3	28	0,0025	0,22	0,065	200
15	4	38	0,005	0,23	0,085	200
16	5	35	0,006	0,24	0,06	210
17	3	38	0,006	0,25	0,09	200
18	2	35	0,007	0,28	0,075	200
19	4	40	0,008	0,30	0,08	210
20	5	45	0,008	0,20	0,075	200
21	3	35	0,006	0,25	0,065	200
22	2	30	0,005	0,25	0,075	210
23	4	40	0,006	0,26	0,3	200
24	4	35	0,007	0,24	0,25	200
25	5	30	0,005	0,25	0,3	210

Учебное издание

РАСЧЕТ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК

Методические указания к выполнению курсовой работы

для студентов специальности ДВС

Составитель: Анатолий Иванович Громовик

Редактор Т.И. Калинина

** *

Подписано к печати 26.10.11 Формат 60 х 90 1/16. Бумага писчая Оперативный способ печати Гарнитура Таймс

Усл. п. л. 1,5, уч.-изд. л. 1,5

Тираж 20 экз. Заказ___

Цена договорная

** *

Издательство СибАДИ 644099, Омск, ул. П.Некрасова

__________________________

Отпечатано в ПЦ издательства СибАДИ 644099, Омск, ул. П.Некрасова

_________________________________

<<< < Предыдущая 1 23 / 33

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021612.62 Кб0640.pdf
#
07.01.2021612.62 Кб0641.pdf
#
07.01.2021612.66 Кб0642.pdf
#
07.01.2021612.66 Кб0643.pdf
#
07.01.2021613.01 Кб3644.pdf
#
07.01.2021613.25 Кб5645.pdf
#
07.01.2021613.89 Кб5646.pdf
#
07.01.2021614.87 Кб25647.pdf
#
07.01.2021615.8 Кб6648.pdf
#
07.01.2021616.05 Кб1649.pdf
#
07.01.2021267.58 Кб065.pdf