
645
.pdf
РАСЧЕТ
ОСЕСИММЕТРИЧНЫХ
ОБОЛОЧЕК
Омск 2011
РАСЧЕТ ОСЕСИММЕТРИЧНЫХ
ОБОЛОЧЕК
Методические указания к выполнению курсовой работы
для студентов специальности ДВС
Составитель: А.И. Громовик
Омск Издательство СибАДИ
2011
УДК 624.08 ББК 38. 114
Рецензент канд. техн. наук, доц. Уткин В.А.
Работа одобрена научно-методическим советом факультета АТ в качестве методических указаний для выполнения курсовой работы по механике материалов и конструкций для студентов механических специальностей.
Расчет осесимметричных оболочек. Методические указания к выполне-
нию курсовой работы для студентов специальности ДВС. Сост. А.И. Громовик. – Омск: Изд-во СибАДИ, 2011. – 32 с.
Содержатся основные положения по расчету на прочность осесимметричных оболочек. Изложены основные положения безмоментной теории расчета оболочек. Представлены методика расчета и последовательность выполнения работы с графической интерпретацией. Даны примеры по моментной теории расчета оболочек различных схем с учетом краевых эффектов. Представлен пример расчета в среде MathCAD. В приложении приведены расчетные схемы и исходные данные по вариантам. Дан список рекомендуемой литературы.
Ил. 13. Библиогр.: 8 назв. Табл. 2.
© Составитель А.И. Громовик, 2011
СОДЕРЖАНИЕ
Введение..…………………………………………………………………………..4
1.Линии и радиусы поверхности оболочки…………..……………………….….4
2.Безмоментная теория осесимметрично нагруженных оболочек……………..4
3.Сферический сосуд под внутренним давлением q……………………………7
4.Цилиндрический котел под внутренним давлением ………………………….7
5.Подвешенный бак с коническим днищем………………………………………8
6.Краевой эффект в цилиндрической оболочке………………………………..10
7.Расчет длинной цилиндрической оболочки(защемление с двух сторон)…..13
8.Расчет цилиндрической оболочки, шарнирно опертой по концам……….. 15
9.Примеры расчета оболочек вращения………………………………………..17
9.1.Цилиндрическая оболочка со сферическим днищем………………………17
9.2.Цилиндрическая оболочка с плоским днищем…………………………...19.
Библиографический список……………………………………………….……..21
Таблица 1. Расчетные схемы оболочек………………………..………….……..22
Таблица 2. Исходные данные………………………………………………….…23
Введение
Оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми незначительно по сравнению с размерами поверхностей.
1. Линии и радиусы поверхности оболочки
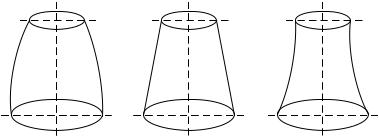
Плоскость, пересекающая поверхность оболочки и проходящая через ось вращения, образует меридиональную линию или меридиан. Линии, перпендикулярные меридианам и оси вращения называют параллелями. Поверхность, равноудаленная от внешней и внутренней поверхностей оболочки, называют срединной и имеющей двуяковую кривизну.
Радиус кривизны меридиана – m ; радиус кривизны параллели
– t . Радиусы m и t – главные радиусы кривизны поверхности вращения. Важное значение при изучении свойств поверхности
имеет гауссова кривизна K |
1 |
. На рис. 1 даны некоторые фор- |
|
||
|
m t |
|
мы меридианов при соответствующих K . |
||
При K 0 – меридианы выпуклые (рис. 1, а); K 0 – меридиа- |
||
ны прямые линии (рис. 1, б); |
K 0 – меридианы вогнутые (рис. 1, |
|
в), при этом, если t 0, то m 0.
а) |
б) |
в) |
|
Рис. 1 |
|
2. Безмоментная теория осесимметрично нагруженных оболочек
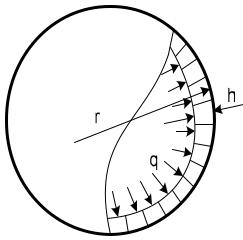
Примером безмоментного состояния служит напряженное состояние, возникающее в оболочке под действием равномерного внутреннего давления. Оболочка испытывает только растяжение. В этом заключается ее преимущество как конструктивного элемента.
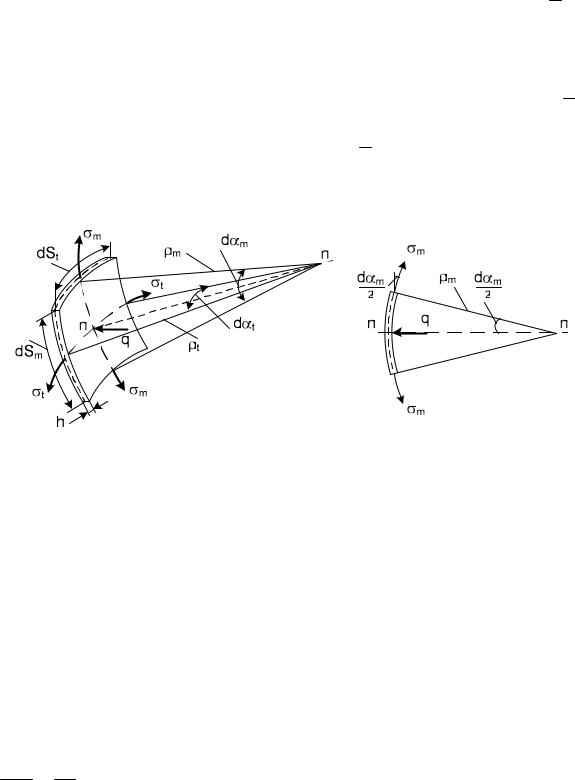
Встенках оболочки возникают нормальные меридиональные
m и окружные t напряжения (рис. 2, а).
Основным признаком безмоментного состояния будет h,
2
где – относительное удлинение срединной поверхности; – относительное изменение кривизны; h – толщина стенки. Так напря-
жение растяжения р E , а напряжение изгиба – и E h ,
2
то, в виду незначительности величины h , напряжением и мож- 2
но пренебречь.
а) |
б) |
Рис. 2 |
|
Рассмотрим равновесие сил, |
возникающих от действия внут- |
реннего давления q на элементарной площади dA dSm dSt и усилий от напряжений меридионального m и тангенциального t с площадями dSt h и dSm h. На рис. 2, б показана меридиональная плоскость. Спроецируем все усилия на общую нормаль n n:
2 m h dSt |
sin |
d m |
2 t |
h dSm |
sin |
d t |
q dSt dSm |
0. (1) |
|
|
|||||||
|
2 |
|
|
2 |
|
|
||
Заменим синус его аргументом ввиду малости угла и разделим выражение (1) на h dSt dSm , получим
|
m |
|
d m |
|
t |
|
d t |
|
q |
, или, с учетом равенства |
d m |
|
1 |
; |
|
|
|
||||||||||||
|
dSt |
|
dSm |
|
||||||||||
|
|
dSm |
|
|
h |
|
m |
|||||||
d t 1 , окончательно определим dSt t
|
|
m |
|
t |
|
|
q |
. |
|
|
|
(2) |
||
|
|
t |
|
|
|
|||||||||
|
|
m |
|
|
|
h |
|
|
|
|||||
Зависимость (2) называют уравнением Лапласа. |
|
|
||||||||||||
Если |
принять dSt dSm 1, |
то |
Nm |
m h 1; |
Nt t h 1 и |
|||||||||
уравнение (2) можно представить как |
Nm |
|
Nt |
q. |
|
(2а) |
||||||||
m |
t |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
и t . Оп- |
|||
В уравнение входят два неизвестных напряжения |
||||||||||||||
ределим |
сначала m , используя |
уравнение |
равновесия |
согласно |
||||||||||
рис. 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 m
m
 m
m 
 t
t
o |
q |
|
m |
||
|
h
Q
r
o
Рис. 3
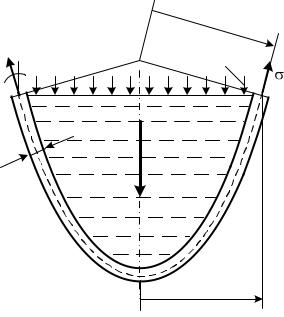
Вырежем часть оболочки вращения, заполненной жидкостью. Q – веса части жидкости и емкости, лежащие ниже рассматриваемого слоя, q– давление в жидкости с учетом избыточного (по закону Паскаля) q H q0 ,
где q0 – избыточное давление в емкости; H – глубина рассматриваемого слоя; – объемный вес жидкости. Площадь окружного се-
чения емкости рассчитаем как: Aокр |
2 r h. |
|
|
|||||||
Спроецируем силы на ось О О: |
|
|
|
|||||||
m 2 r h cos m q r2 |
Q 0. |
|
(3) |
|||||||
Отсюда: |
|
m |
|
q r |
|
|
Q |
. |
(4) |
|
2h cos m |
2 r h cos m |
|||||||||
|
|
|
|
|
|
|||||
Подставив (4) в уравнение (2), определим t . Рассмотрим конкретные расчетные схемы.
3. Сферический сосуд под внутренним давлением q
Рис. 4
Считаем, что m t , а m t r (рис. 4), определим
|
|
q r |
. |
|
|
|
|
|
|
(5) |
||
|
|
|
|
|
|
|
||||||
|
|
|
2h |
|
|
|
|
|
||||
Согласно закона Гука для плоского деформированного состоя- |
||||||||||||
ния, относительная |
радиальная |
деформация |
t |
|
1 |
t |
m . В |
|||||
|
||||||||||||
|
2 r w 2 r |
|
|
w |
|
|
|
E |
|
|||
нашем примере t |
|
, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||
|
2 r |
|
|
|
|
r |
|
|
|
|
|
|
где w – абсолютное приращение радиуса сферы под давлением q. Считая t m , с учетом (5) и выражениях относительных
деформаций, определим абсолютную деформацию
|
w |
|
1 |
|
|
1 . |
|
||||
|
|
|
|
|
|
|
|||||
|
r E |
|
E |
|
|
||||||
Таким образом, w |
r |
1 |
q r2 |
1 . |
(6) |
||||||
|
2E h |
||||||||||
|
|
|
E |
|
|
||||||
4. Цилиндрический котел под внутренним давлением
Рис. 5
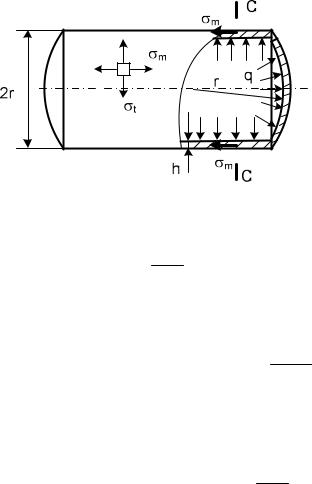
Меридианами считаем образующие котла (см. рис.5), т. е.
q r
m ; t r, следовательно t h .
Меридиональное напряжение определим, рассматривая равновесие правой отсеченной части котла по сечению C C.
m 2 r q r2 0, или m q r2 . 2h
Следовательно, окружное напряжение в два раза больше меридионального. Используя выкладки предыдущего примера, выразим абсолютное радиальное перемещение
|
|
w |
|
1 |
t m |
|
1 |
q r |
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
r |
|
E |
|
h |
||||||||
|
|
|
|
|
|
|
|
E |
|
|||||
Отсюда, w |
q r2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
. |
|
|
|
|
|
||||
E h |
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|||||
q r
. 2h
(7)
5. Подвешенная цилиндрическая оболочка с коническим днищем
Наполнена жидкостью объемным весом , (см. рис. 6). Определить напряжения t , m в цилиндрической и кониче-
ской частях, построить эпюры напряжений.
Начало вертикальной координаты x в днище оболочки; ry – текущий радиус конической части; 2 – угол конуса днища.
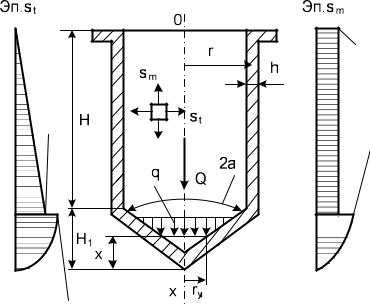
Рассмотрим коническую часть.
Давление жидкости на глубине |
H H1 x |
равно |
q H H1 x .
|
|
Т. к. |
m |
, t |
q t |
. Проекция |
t |
на горизонтальную ось |
|||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
ry |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
x |
|
||
|
|
|
|
. Выразим r |
|
через радиус оболочки r r |
|
||||||||||||||
t |
|
|
y |
|
. Окружное |
||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
y |
H1 |
|
|||||
напряжение конической части примет вид: |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
t |
q |
r |
|
x |
|
|
r |
|
x |
|
H H1 x . |
(8) |
|||
|
|
|
|
|
|
|
H1 cos |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
h |
|
h H1 |
cos |
|
|
|
||||||||
mц |
tц |
mк |
tк
|
|
|
|
|
|
Рис. 6 |
|
|
|
|
|
|
|
|
|
При x H1; t |
|
|
|
r |
H |
; при |
x H H1 |
; |
t |
0 |
(см. |
||||
к |
|
|
|||||||||||||
эп. t , рис. 6). |
|
h |
cos |
|
|
|
|
|
|
ц |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цилиндрическая часть. |
|
q ry |
|
|
|
|
|
|
|
||||||
Воспользуемся уравнением (4): m |
|
|
|
|
|
Q |
|
. |
|||||||
2h cos |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2h r cos |
|||||
Выразим q через объемный вес, ry – через радиус оболочки.
