1.5. Методические указания к выполнению контрольной работы 1

Задачи № 1 – 11

Задачи составлены по разделам технической термодинамики: уравнение

состояния идеального газа, смесь идеальных газов, теплоемкость, первый закон 14

термодинамики и основные термодинамические процессы. При решении этих задач могут быть использованы следующие формулы и выражения.

Уравнение состояния идеального газа [2 – 8]:

для 1 кг –

pv RT ;

(1.1)

для G кг –

pv GRT ,

(1.2)

где v – удельный объем идеального газа, м³/кг; R = 8314/μ – газовая постоянная, Дж/(кг∙К);

• – масса 1 моля газа, кг (численно равна молекулярной массе газа); р – абсолютное давление, Па:

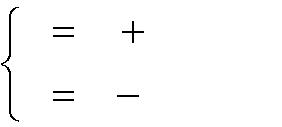
p	B	pм	;	(1.3)
p	B	pв ,

где р_м – избыточное давление, измеряемое манометром, Па; р_в – разряжение, измеряемое вакуумметром, Па;

• – атмосферное (барометрическое) давление (В = 750 мм рт. ст. ≈10⁵ Па), Па. Для газовых смесей вводят понятие о так называемой средней (кажущей-

ся) молекулярной массе смеси, значение которой определяется по выражениям:

через объемные доли [3] –

	n
см	ri i ,	(1.4)
	1

и через массовые доли –

n
см 1 / mi i ,	(1.5)
1
15

где μ_i – молекулярная масса компонента, входящего в смесь, кг/кмоль;

m	i	Gi	– массовая доля газа в смеси (отношение массы этого газа, входя-
		G

щего в смесь, к массе всей смеси), кг;

r	Vi	– объемная доля (отношение приведенного объема какого–либо
i	V
газа, входящего в смесь, к объему всей смеси).
Формулы пересчета состава смеси [4 – 6]:
		ri	miμсм / μi ;	(1.6)
		mi	ri i / см ,	(1.7)

Газовую постоянную смеси идеальных газов R можно определить или че-рез газовые постоянные отдельных компонентов R_i, входящих в смесь,

n

18. m_i R_i , или по средней молекулярной массе смеси R = 8314/μ_см, Дж/(кг∙К).

1

Для определения парциального давления отдельного компонента p_i, вхо-

дящего в смесь, служат формулы p		r p и p	i	m	i	Ri	p , где р – полное давление
	i	i				R
смеси газов, Па.

• зависимости от выбранной количественной единицы вещества разли-

чают мольную теплоемкость μс, кДж/(кмоль∙К), массовую – с, кДж/(кг∙К), и

объемную – с´, кДж/(м³∙К). Объемную теплоемкость относят к 1 м³ при нор-мальных физических условиях (р_о = 760 мм рт. ст. = 101325 Па, t_о = 0 °С). Эти теплоемкости связаны между собой следующими зависимостями:

c		c c				;	(1.8)
					0
c		c			c	0 ,	(1.9)
	22, 4

где μ – молекулярная масса газа, кг/кмоль;

16

1. – плотность газа при нормальных физических условиях, кг/м³.

Мольная, массовая и объемная теплоемкости могут быть при постоянном давлении с_р и при постоянном объеме с_v. Отношение теплоемкостей при посто-янном давлении и постоянном объеме называют показателем адиабаты и обо-

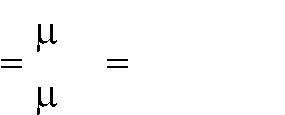
значают буквой k, т. е. k	c p		cp	.
	c v		cv

Теплоемкость газа зависит от его температуры. В приближенных расче-тах часто пренебрегают этой зависимостью и теплоемкость газов одинаковой атомности считают величиной постоянной. Значения мольных теплоемкостей и показателей адиабаты приведены в табл. 3.

		Т а б л и ц а 3
Значения мольных теплоемкостей и показателей адиабаты
Газы	Удельная мольная теплоемкость, кДж/(кмоль∙К)			k
	μсp	μсv
Одноатомные	12,56	20,93		1,67
Двухатомные	20,93	29,31		1,40
Трех- и многоатом-	20,31	37,68		1,29
ные

Зависимости теплоемкостей газов от температуры имеют нелинейный ха-рактер. В источнике [7] в табл. П.1 приведены средние мольные теплоемкости некоторых газов в пределах от 0 до t, ^оС. При пользовании данными указанной таблицы в необходимых случаях требуется производить интерполяцию.

Для смесей идеальных газов [5, 6] теплоемкость определяется по формулам:

массовая –

	n
ссм	mi c ;	(1.10)
	1

объемная –

	n
cсм	ri ci ;	(1.11)
	1
	17

мольная –

	n
cсм	ri ci .	(1.12)
	1

Для определения, например, средней мольной теплоемкости в пределах температуры от t₁ до t₂ надо из соответствующей таблицы взять теплоемкость c_m1 и c_m2 соответственно в пределах (0 – t₁) ^оС и (0 – t₂) ^оС (средние теплоем-

кости помечаются индексом m). Затем по выражению	cm	c m t 2	c m t1	рас-
		2	1
		t 2	t1

считать искомую теплоемкость.

Если в процессе участвуют G кг вещества, то количество теплоты в соот-ветствующем процессе определяется по выражению [7]:

Q G(c m	t	2	c m t 1 ) .	(1.13)
	2		1

• pv-диаграмме линия, изображающая политропный процесс, строится в

соответствии с уравнением pvⁿ = const, где n – показатель политропы. Связь между основными параметрами рабочего тела в политропном процессе выра-жается следующими формулами:

p	/ p	2		v		/ v		2	n ;		(1.14)
1					1
T	/ T			v	1	/ v	2		n-1 ;		(1.15)
2	1
									n-1		(1.16)
T2 / T1			p1 / p2							.
									n

Для адиабатного процесса в формулах (1.14) – (1.16) показатель n заменя-ется показателем адиабаты k = с_p/c_v.

18

Изменение внутренней энергии u_{1 2} , энтальпии h_{1 2} и энтропии s_{1 2} не зависит от характера процесса и при постоянной теплоемкости 1 кг идеаль-ного газа подсчитывается по формулам:

Δu1-2	u2	u1	cv t 2	t1	;		(1.17)
Δh1-2	h 2	h1	cp t 2	t1	;		(1.18)
Δs1-2	s2	s1	cln T2 / T1 .			(1.19)

• выражении (1.19) с – теплоемкость соответствующего процесса. Для политропного процесса теплоемкость [5]

c n cv	n	k
			.	(1.20)
	n	1

Работа газа в политропном процессе, кДж,

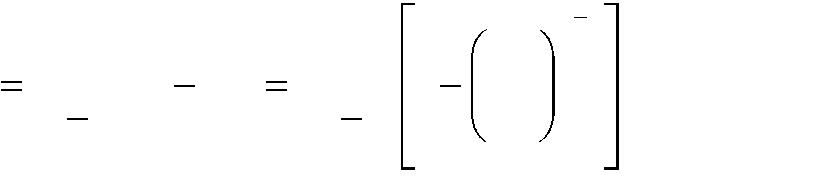
n

1

L

GR (T1 T2 )

GRT1 1

p2

n

.

(1.21)

n 1

n 1

p1

• изотермическом процессе по первому закону термодинамики теплота равна работе процесса и может быть определена по формуле:

Q L GRTln	v2	GRTln	p1	.		(1.22)
	v1
			p2

В этом процессе изменение удельной энтропии [5]

s1 2	s2s1	R ln	v2	R ln	p1		q1 2	,	(1.23)
			v1		p2		T

где q		Q	.
	2
1		G

19

• адиабатном процессе удельная работа равна изменению внутренней энергии с обратным знаком:

l L / G u1 u2 cv (t1 t2 ) .

(1.24)

Задачи № 12 – 18

Задачи решаются при помощи hs-диаграммы водяного пара, практическая часть которой состоит из двух областей [1]. Ниже пограничной кривой сухого насыщенного пара (степень сухости х = 1) будет область влажного насыщенно-го пара (0 < х < 1), выше – область перегретого пара. Поэтому, когда в задаче требуется определять состояние пара, нужно показать, в какой области диа-граммы находится точка данного состояния пара. В hs-диаграмме в области влажного пара соответствующие изобара и изотерма совпадают, так как в этой области определенному давлению соответствует определенная температура на-сыщения. В области перегретого пара изотермы отклоняются от изобар вправо, асимптотически приближаясь к горизонтальной линии.

Удельная внутренняя энергия пара u = h – pv (здесь необходимо обратить внимание на соответствие размерностей всех величин).

Удельная теплота в изобарном процессе равна изменению энтальпии в этом процессе, т. е. q_1-2 = h₂ – h₁. В изотермическом процессе q_1-2 = T(s₂ – s₁).

• обратимом адиабатном процессе изменения состояния пара, протекаю-щем при постоянном значении энтропии, удельная работа l_1-2 = u₁ – u₂ =

• (h₁ – p₁v₁) – (h₂ – p₂v₂).

Процесс дросселирования пара условно изображается линией постоянной энтальпии.

Для влажного насыщенного пара [2 – 5] – удельный объем

vx v x v (1 x) ; энтальпия hx h rx ; энтропия sx s rx / Tн ; внутренняя

энергия

ux

hx

pvx .

Задачи № 19 – 22

Задачи составлены на процессы истечения и дросселирования газов и па-ров. Процесс истечения принимается без теплообмена, т. е. адиабатным, для ко-торого в указаниях к задачам 1 – 11 приведены формулы, связывающие основ-

20

ные параметры идеального газа, и неразрывным (сплошным), когда соблюдает-ся равенство (уравнение неразрывности):

Gv fc ,

(1.25)

где G – массовый расход газа или пара, кг/с;

22. – удельный объем газа или пара, м³/кг; f – площадь данного сечения сопла, м²;

с – скорость потока в рассматриваемом сечении, м/с.

По равенству (1.25) можно определять массовый расход или площадь данного сечения сопла.

Если адиабатное истечение газа или пара происходит при отношении давлений р₂/р₁ больше критического значения (р₂/р₁)_кр, то применяют сужи-вающееся сопло. В этом случае теоретическая скорость истечения определяется по формуле, м/с [7]:

			k							k 1
													(1.26)
c	2	2				BT 1	(p	2	/p ) k
			k	1		2			1

Для водяного пара скорость истечения определяют по выражению:

c ₂ 44,76 h₁ h₂ , (1.27)

где h₁ и h₂ – соответственно энтальпия, кДж/кг, пара в начале и в конце адиабат-ного процесса истечения, значения энтальпии определяются по hs-диаграмме.

Критическое отношение давлений для двухатомных газов, в том числе для воздуха (k = 1,4), равно 0,528, а для перегретого водяного пара – 0,546.

Если истечение происходят при р₂/р₁ < (р₂/р₁)_кр, то применяют расши-ряющееся сопло Лаваля, где скорость в выходном сечении сопла достигает сверхкритических (сверхзвуковых) значений. В этом случае скорость на выходе из сопла определяется по формулам (1.26) – (1.27), а критическая скорость в минимальном сечении для двухатомных газов – по формуле:

21

cкр 1,08 p1v1 ,			(1.28)

или

cкр 1,08 RT1

(1.29)

Для перегретого пара:

c кр 44, 76 h 1 hкр ,

(1.30)

где h_кр – энтальпия пара в минимальном сечении сопла в конце адиабатного процесса расширения пара до критического давления р_кр = 0,546р₁, определяет-ся по hs-диаграмме.

Площадь минимального сечения Лаваля может быть определена по урав-нению неразрывности потока:

fmin	Mvкр	,	(1.31)
	cкр

где v	кр	v (p / p	кр	)1/k	– для газов.
		11

Величина v_кр для пара может быть определена по hs-диаграмме.

Задачи № 23 и 24

При политропном сжатии работа одноступенчатого идеального компрес-сора определяется по выражению [5], кДж/с:

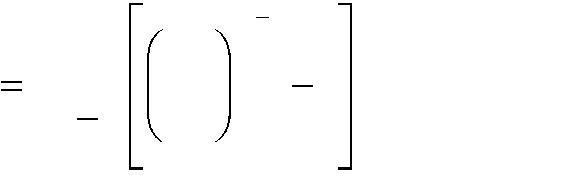
					m 1
	p1 v1		p2
					m
L				1 ,			(1.32)
	m 1		p1

где р₁ и р₂ – абсолютное давление в процессах всасывания и нагнетания, кПа; V₁ = V_nn – подача компрессора при условиях всасывания, м³/с.

22

Теоретическая мощность привода компрессора в m раз больше L, т. е.

N_т = m ∙ L.

Работа, отнесенная к 1 м³ всасываемого газа, кДж/м³,

	m		m 1
l					1 ,	(1.33)
	m 1 p1		m

где для одноступенчатого компрессора β = р₂/р₁ для двухступенчатого – l = l_I + l_II.

При определении lI и lII _I p _пром / р₁ , _II p ₂ / p_пром .

Задачи № 25 – 29

Цикл вычерчивается в pv- и Ts-диаграммах с обозначением всех переход-ных точек цикла. Так как в теоретических циклах поршневых двигателей внут-реннего сгорания и газотурбинных установках процессы сжатия и расширения являются адиабатными, то основные параметры в точках этих процессов могут быть определены по зависимостям между начальными и конечными парамет-рами адиабатного процесса (см. указания к задачам 1 – 11).

• задачах 26 и 27 неизвестные значения температуры в соответствующих точках процесса определяются по формуле теплоты данного процесса. В ряде точек цикла неизвестный параметр состояния рабочего тела определяется по

уравнению состояния идеального газа. Если в данной задаче определены тер-мический КПД η_t и удельная полезная работа l_о, то удельное количество подве-денной теплоты в цикле q₁ = l₀/η_t, а отведенной – q₂ = q₁ – l₀.

Задача № 30

Термический КПД теоретического паросилового цикла (цикла Ренкина)

t	h1	h	2	,	(1.34)
	h1	h	2

где h₁ – энтальпия пара в начале адиабатного процесса расширения пара в па-ровом двигателе. Значение h₁ определяется по hs-диаграмме по заданным на-чальным параметрам пара [1];

23

h₂ – энтальпия пара в конце адиабатного процесса расширения пара (точка

2. находится на пересечении линии расширения s₁ = const с изобарой р₂ заданно-го давления в конденсаторе);

h₂ – энтальпия кипящей жидкости (конденсата) при заданном давлении в

конденсаторе.

Контрольная работа 2

ОСНОВЫ ТЕПЛОПЕРЕДАЧИ