
- •Структурный, кинематический и силовой анализ механизма синтез зубчатой передачи
- •1 Структурный анализ механизма
- •1.1 Определение степени подвижности плоского механизма
- •1.2 Определение класса механизма
- •2 Кинематическое исследование плоских механизмов
- •2.1 Основные задачи и методы кинематического исследования механизмов
- •2.2 Построение планов положений механизмов
- •2.3 Построение траектории точек
- •2.4 Определение скоростей точек механизма методом планов скоростей
- •2.5 Определение ускорений точек механизма методом планов ускорений
- •3 Силовое исследование механизмов
- •4 Геометрический синтез прямозубого внешнего зацепления
- •4.1 Определение размеров, качественных характеристик и вычерчивание нулевого зацепления
- •4.2 Определение качественных показателей зацепления Качественные показатели зацепления – коэффициенты перекрытия ε.
2.5 Определение ускорений точек механизма методом планов ускорений
При помощи планов ускорений можно найти ускорение любых точек механизма. Для построения планов ускорений по аналогии с планами скоростей следует пользоваться их свойствами. Свойства такие же, как и у планов скоростей, кроме третьего, где фигура, подобная одноимённой жёсткой фигуре на плане положений механизма, повёрнута на угол (180 ̊‒φ')в сторону мгновенного ускоренияε данного звена.
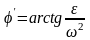 (2.16)
(2.16)
Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то концы векторов абсолютных ускорений обозначают буквами, соответствующими названию точек.
Считая известными
ускорения шарнирных точек (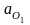 =
=
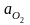 =
0), помещаем их на плане ускорений в
полюсе Ра. Звено О1А вращается
равномерно, поэтому точка А имеет только
нормальное ускорение
=
0), помещаем их на плане ускорений в
полюсе Ра. Звено О1А вращается
равномерно, поэтому точка А имеет только
нормальное ускорение
 ,
которое направлено по звену О1А
к центру вращения О1. Определяем
его по формуле 2.17:
,
которое направлено по звену О1А
к центру вращения О1. Определяем
его по формуле 2.17:
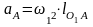 , (2.17)
, (2.17)
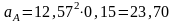 м/с2
м/с2
Масштаб плана ускорений по формуле 2.3:
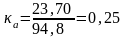 м/с2
∙ мм-1
м/с2
∙ мм-1
По аналогии с планом ускорений составляем векторные уравнения для определения ускорений точки В:
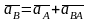 (2.18)
(2.18)
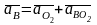 (2.19)
(2.19)
Определим величину нормального ускорения, м/с2:
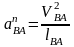 , (2.20)
, (2.20)
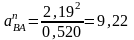 м/с2
м/с2
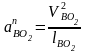 , (2.21)
, (2.21)
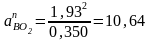 м/с2
м/с2
Величины векторов нормальных ускорений определяем с помощью масштаба, мм:
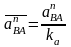 ,
(2.22)
,
(2.22)
 , (2.23)
, (2.23)
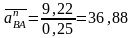 мм
мм
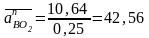 мм
мм
Определим место точки «с» на плане ускорений:
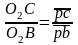 , (2.24)
, (2.24)
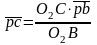
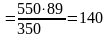 мм,
мм,
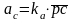 , (2.25)
, (2.25)
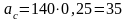 м/с2.
м/с2.
По аналогии с планом скоростей определяем положение точек S1,S2, S3, используя масштаб, рассчитаем ускорения всех точек механизма, м/с2:
 , (2.26)
, (2.26)
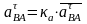 , (2.27)
, (2.27)
 , (2.28)
, (2.28)
 ,
(2.29)
,
(2.29)
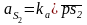 , (2.30)
, (2.30)
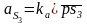 . (2.31)
. (2.31)
Подставляя числовые значения, получаем:
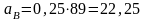 м/с2,
м/с2,
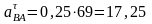 м/с2.
м/с2.
 м/с2.
м/с2.
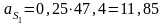 м/с2.
м/с2.
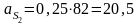 м/с2.
м/с2.
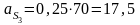 м/с2.
м/с2.
Угловое ускорениедля второго и третьего звеньев:
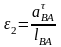 , (2.32)
, (2.32)
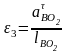 , (2.33)
, (2.33)
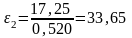 с-2.
с-2.
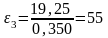 с-2.
с-2.
Для определения направления углового
ускорения
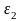 звена
AB надо мысленно перенести
вектор тангенциального ускорения
звена
AB надо мысленно перенести
вектор тангенциального ускорения
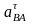 в
точку B звена AB.
В направлении этого вектора точка В
вращается относительно точки А против
хода часовой стрелки. Для определения
углового ускорения
в
точку B звена AB.
В направлении этого вектора точка В
вращается относительно точки А против
хода часовой стрелки. Для определения
углового ускорения
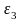 звена BC вектор
тангенциального ускорения
звена BC вектор
тангенциального ускорения
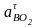 следует
мысленно перенести в точку B
звена 3. Угловое ускорение
направлено
по ходу часовой стрелки.
следует
мысленно перенести в точку B
звена 3. Угловое ускорение
направлено
по ходу часовой стрелки.
3 Силовое исследование механизмов
В задачу силового исследования входит определение:
1) сил, действующих на звенья механизма;
2) реакций в кинематических парах;
3) уравновешивающей силы (момента).
Силовой анализ основан
на принципе Даламбера. Сущность его
заключается в том, что каждое звено
может рассматриваться в условном
статистическом равновесии, если к нему
помимо всех действующих внешних сил
приложить инерционную нагрузку в виде
силы инерции и момента пары сил инерции,
при этом условии для каждого звена
справедливы равенства и
и
 ,
поэтому неизвестные силы (реакции в
кинематических парах) могут определяться
методом статики.
,
поэтому неизвестные силы (реакции в
кинематических парах) могут определяться
методом статики.
Для проведения силового анализа кинематическая цепь должна быть статически определимой, т.е. число неизвестных параметров реакций должно быть равно количеству уравнений статики, которые можно составить для их определения.
Начинать силовой анализ необходимо с наиболее удалённой от ведущего звена структурной группы.
С помощью заданного веса одного миллиметра длины звена q = 0,3 Н/мм определяем вес звеньев механизма:
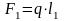 ,
(3.1)
,
(3.1)
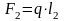 , (3.2)
, (3.2)
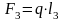 , (3.3)
, (3.3)
 Н.
Н.
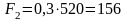 Н.
Н.
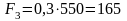 Н.
Н.
Массы звеньев:
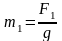 ,
(3.4)
,
(3.4)
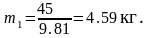
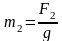 ,
(3.5)
,
(3.5)
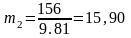 кг,
кг,
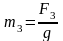 , (3.6)
, (3.6)
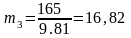 кг.
кг.
Силы инерции:
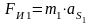 ,
(3.7)
,
(3.7)
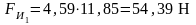 ,
,
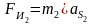 , (3.8)
, (3.8)
 ,
,
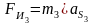 , (3.9)
, (3.9)
 .
.
Вычисляем момент сил инерции звена АВ:
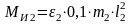 , (3.10)
, (3.10)
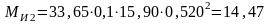 Н ∙ м ,
Н ∙ м ,
Вычисляем момент сил инерции звена О2С:
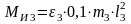 , (3.11)
, (3.11)
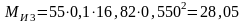 Н ∙ м ,
Н ∙ м ,
Изображаем группу Ассура 2-3 и прикладываем к ней все силы. Освобождаем группу от связей и прикладываем вместо них реакции F43 в шарнире О2 и F12в шарнире А. Реакцию F12 представляем в виде двух составляющих F12τ и F12n. Реакцию F43 представляем в виде двух составляющих F43τ и F43n.
Составляем уравнение моментов всех сил относительно точки В для каждого звена отдельно, для звена АВ и для звена О2С:
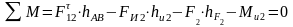 ,
(3.12)
,
(3.12)
 Н.
Н.
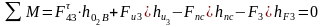 ,
(3.13)
,
(3.13)
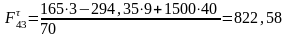 Н
Н
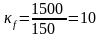 Н/мм
Н/мм
Составляем векторное уравнение равновесия всех сил и строим многоугольник сил, принимая масштаб плана сил kF=10 Н/мм:
 ,
(3.14)
,
(3.14)
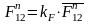 , (3.15)
, (3.15)
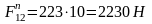
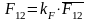 , (3.16)
, (3.16)

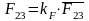 , (3.17)
, (3.17)
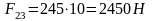
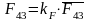 ,
(3.18)
,
(3.18)

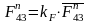 , (3.19)
, (3.19)
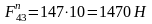
Силы F12 и F21 равны по модулю, но противоположны по направлению. И силы F23и F32 тоже равны по модулю, но противоположны по направлению.
Расчёт ведущего звена начинаем с изображения звена О1А и приложим к нему все действующие силы, а в точку А приложим уравновешивающую силу, перпендикулярно звену АВ в направлении вращения.
Составляем уравнение моментов всех сил относительно точки О1 и найдём уравновешивающую силу, Н:
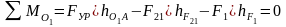 ,
(3.20)
,
(3.20)
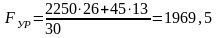 Н.
Н.
Найдем масштаб ведущего звена по формуле:

 (3.21)
(3.21)
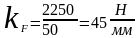
Составляем векторное уравнение и строим план сил, принимая масштаб плана сил kF = 45 Н/мм:
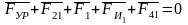 ,
(3.22)
,
(3.22)
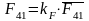 (3.23)
(3.23)
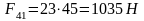 .
.
