
- •Структурный, кинематический и силовой анализ механизма синтез зубчатой передачи
- •1 Структурный анализ механизма
- •1.1 Определение степени подвижности плоского механизма
- •1.2 Определение класса механизма
- •2 Кинематическое исследование плоских механизмов
- •2.1 Основные задачи и методы кинематического исследования механизмов
- •2.2 Построение планов положений механизмов
- •2.3 Построение траектории точек
- •2.4 Определение скоростей точек механизма методом планов скоростей
- •2.5 Определение ускорений точек механизма методом планов ускорений
- •3 Силовое исследование механизмов
- •4 Геометрический синтез прямозубого внешнего зацепления
- •4.1 Определение размеров, качественных характеристик и вычерчивание нулевого зацепления
- •4.2 Определение качественных показателей зацепления Качественные показатели зацепления – коэффициенты перекрытия ε.
2.2 Построение планов положений механизмов
Планом положения механизма называется чертёж, изображающий расположение его звеньев в какой-то определённый момент движения. Отсюда следует, что план положения представляет собой кинематическую схему механизма, вычерченную для заданного положения механизма.
Построение плана
начинается с нанесения элементов
неподвижного звена (точек опор О1
и О2). Под углом
 точки О1 проводим ось ведущего
звена и от точки О1 откладываем
на ней отрезок О1А, равный длине
кривошипа.
точки О1 проводим ось ведущего
звена и от точки О1 откладываем
на ней отрезок О1А, равный длине
кривошипа.
Затем определяем положение точки В. Для этого из точки А радиусом АВ и точки О2 радиусом ВО2 делаем засечки. На продолжении звена О2В находим положение точки С.
2.3 Построение траектории точек
Для построения траектории какой-либо точки необходимо построить несколько планов положений механизма, найти на каждой из планов положение заданной точки и соединить их последовательно плавной кривой.
2.4 Определение скоростей точек механизма методом планов скоростей
Зная закон движения ведущего звена и длину каждого звена механизма, можно определить скорости его точек по значению и направлению в любом положении механизма путём построения плана скоростей для этого положения. Значения скоростей отдельных точек механизма необходимы при определении производительности и мощности машины, потерь на трение, кинетической энергии механизма; при расчёте на прочность и решении других динамических задач.
Построение планов скоростей и чтение их упрощают при использовании свойств этих планов:
1) векторы, проходящие через полюс РV, выражают абсолютные скорости точек механизма. Они всегда направлены от полюса. В конце каждого вектора принято ставить малую букву a, b, c… или другую. Точки плана скоростей, соответствующие неподвижным точкам механизма, находятся в полюсе РV (О1, О2);
2) векторы, соединяющие концы векторов абсолютных скоростей, не проходящие через полюс, изображают относительные скорости. Направлены они всегда к той букве, которая стоит первой в обозначении скорости;
3) каждое подвижное звено механизма изображается на плане скоростей соответствующим одноимённым, подобным и сходственно расположенным контуром, повёрнутым относительно схемы механизма на 90̊ в сторону мгновенного вращения данного звена. Это свойство плана называется свойством подобия и позволяет легко находить скорость точек механизма.
Определяем угловую скорость кривошипа О1А, по формуле:
 ,
(2.4)
,
(2.4)
где n – частота вращения кривошипа, об/мин

Находим скорость точки А кривошипа, м/с, по формуле:

 , (2.5)
, (2.5)
где  –
длина кривошипа, м.
–
длина кривошипа, м.
 м/с.
м/с.
Вектор скорости точки А направлен перпендикулярно к оси звена О1А в сторону вращения. Масштаб плана скоростей определяем задавшись длиной отрезка, изображающего скорость точки А по формуле 2.2:
 м/с ∙ мм-1
м/с ∙ мм-1
От точки P,
принятой за полюс плана скоростей,
откладываем отрезок
 перпендикулярно О1А.
перпендикулярно О1А.
Из теоретической механики известно, что скорость любой точки звена может быть представленной в виде геометрической суммы переносной и относительной скоростей. Воспользуемся векторными уравнениями:
 ,
(2.6)
,
(2.6)
где 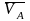 –
скорость точки А,
–
скорость точки А,
 –
относительная скорость точки В во
вращении вокруг точки А.
–
относительная скорость точки В во
вращении вокруг точки А.
 , (2.7)
, (2.7)
где  – скорость точки О2,
– скорость точки О2,
 – относительная скорость точки В во
вращении вокруг точки О2.
– относительная скорость точки В во
вращении вокруг точки О2.
В этих уравнениях
известна по величине и направлению;
 =
0;
=
0;
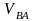 и
и
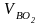 –
лишь по линиям действия:
перпендикулярна к звену АВ;
–
к звену ВC. Поэтому для
определения скорости точки В через
точку а на плане скоростей проводим
линию действия
перпендикулярно к звену АВ, а через
точку О2 (в полюсе P)
– линию действия
перпендикулярно
звену ВC. На пересечении
этих двух линий действия получим точку
в конец вектора скорости
–
лишь по линиям действия:
перпендикулярна к звену АВ;
–
к звену ВC. Поэтому для
определения скорости точки В через
точку а на плане скоростей проводим
линию действия
перпендикулярно к звену АВ, а через
точку О2 (в полюсе P)
– линию действия
перпендикулярно
звену ВC. На пересечении
этих двух линий действия получим точку
в конец вектора скорости
 точки В.
точки В.
 (2.8)
(2.8)
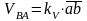 (2.9)
(2.9)
Подставляем численные значения в формулы 2.8 и 2.9:
 м/с
м/с
 м/с
м/с
Определяем угловые скорости звеньев АВ и ВC:
 (2.10)
(2.10)
 с-1
с-1
 (2.11)
(2.11)
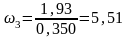 с-1
с-1
Для нахождения отрезка
 составим пропорцию:
составим пропорцию:
 ; (2.12)
; (2.12)


Находим истинные
значения
 по формулам:
по формулам:
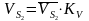 (2.13)
(2.13)

 (2.14)
(2.14)

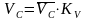 (2.15)
(2.15)

Для определения
направления угловой скорости звена АВ вектор скорости
звена АВ вектор скорости
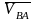 ,
направленной к точке B
плана, мысленно переносим в точку В 2
звена. В направлении этого вектора
точка В вращается относительно точки
А против хода часовой стрелки. Для
определения направления угловой
скорости
,
направленной к точке B
плана, мысленно переносим в точку В 2
звена. В направлении этого вектора
точка В вращается относительно точки
А против хода часовой стрелки. Для
определения направления угловой
скорости
 звена
ВС надо мысленно перенести в точку В 3
звена вектор скорости
.
В направлении этого вектора точка B
вращается относительно точки C
против часовой стрелки.
звена
ВС надо мысленно перенести в точку В 3
звена вектор скорости
.
В направлении этого вектора точка B
вращается относительно точки C
против часовой стрелки.
