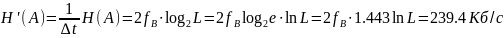3.5. Модулятор

3.5.1. Сглаживающий формирующий фильтр

В состав модулятора входят блоки:

1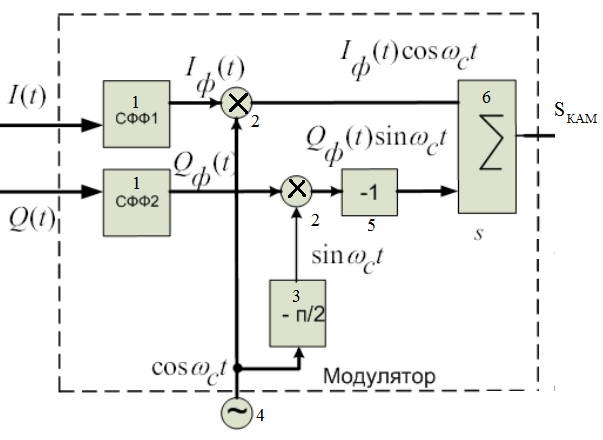 – сглаживающие формирующие фильтры (СФФ1, СФФ2); 2 – перемножители; 3 – фазовращатель; 4– генератор гармонических колебаний; 5– инвертор; 6 – сумматор;

Рис. 17 Структурная схема модулятора

Требуется:

1. Построить графики гармонических колебаний  cosω_ct и sinω_ct на четырех символьных интервалах T_s (n=0, n=1, n=2, n=3). При этом на символьном интервале длительностью T_s укладывается два периода частоты ω_c.

Рис.18 Графики гармонических колебаний sin(wt) и cos(wt)

2. На этих же интервалах T_s нарисовать графики сигналов

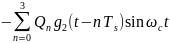
Рис. 19 Графики сигналов

3. На этих же интервалах T_s изобразить график сигнала заданной квадратурной модуляции на выходе сумматора в квазигармонической форме.

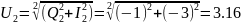
Рис.20 График сигнала заданной квадратурной модуляции

4. Написать аналитические выражения для корреляционных функций B_Icos(τ) B_Qsin(τ) , для случайных сигналов I(t)ꞏcos(ω_Ct+ φ_С) и Q(t)ꞏsin(ω_Ct+ φ_С) на выходах перемножителей, где φ_С случайная фаза с равномерной плотностью вероятности на интервале 0..2π . Случайная фаза не зависит от случайных процессов Q(t) и I(t).

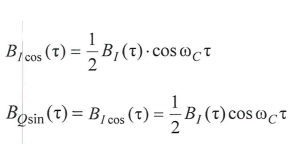
5. Написать аналитические выражения для корреляционной функции сигнала B_S(τ) и для спектральной плотности мощности G_S(ω) сигнала s(t) заданного вида квадратурной модуляции на выходе сумматора. Построить графики этих функций.

Рис. 21 Корреляционная функция сигнала B_S(τ) и спектральная плотность мощности G_S(ω) сигнала s(t) заданного вида квадратурной модуляции на выходе сумматора

3.6. Непрерывный канал

Передача сигнала s_КАМ(t) происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии аддитивной помехи типа гауссовского белого шума. Сигнал на выходе такого канала имеет вид

z(t) = μꞏs_КАМ(t) + n(t),

где μ – коэффициент передачи канала. Для всех вариантов принять μ = 1. Односторонняя спектральная плотность мощности помехи равна N₀.

Требуется:

1. Определить минимальную необходимую ширину полосы частот непрерывного канала.

2. Определить мощность помехи на выходе канала.

Для определения мощности помехи используем график спектральной плотности мощности помехи .

Рис. 22 Спектральная плотность мощности помехи на положительной полуоси частот

Мощность помехи в полосе часто непрерывного канала равна заштрихованной площади, т. е.

3. Определить среднюю мощность сигнала s_КАМ(t) и найти отношение .

Средняя величина энергии определяется

Где и – математические ожидания случайных величин

Аналогично для

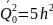
Тогда

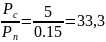
4. Рассчитать пропускную способность С (за секунду) непрерывного канала

5. Оценить эффективность использования пропускной способности непрерывного канала

Для оценки эффективности использования пропускной способности канала связи применяют коэффициент эффективности, равный отношению производительности источника H’ к пропускной способности канала, т. е.