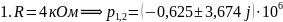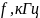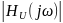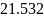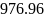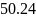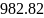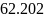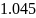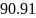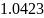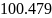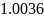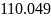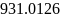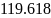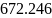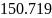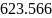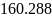ЛАБЫ 4 семестр / ЛАБ 12 / 8363_NersisyanA_LAB_12_2
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОЭ
отчет
по лабораторной работе №12
по дисциплине «Теоретические основы электротехники»
Тема: Исследование искажений импульсных сигналов при прохождении их через линейные цепи
Студент гр. 8363 |
|
Нерсисян А.С. |
Преподаватель |
|
Константинова Е.В. |
Санкт-Петербург
2020
Цель работы
Изучение характера и степени искажений импульсных сигналов прямоугольной формы при прохождении их через линейные цепи.
Краткие теоретические сведения
При исследовании искажений импульсных сигналов обычно через цепь пропускают сигнал прямоугольной формы. Более «гладкие» сигналы той же длительности имеют меньшую ширину спектра и, следовательно, искажаются слабее, чем прямоугольные импульсы. Искажения проявляются в удлинении передних и задних фронтов импульсов, в колебаниях на переднем и заднем фронтах (появление «выбросов»), в спаде плоской части импульсов.
Для оценки искажений используют два основных подхода:
1) в цепях первого и второго порядков, где корни характеристического уравнения (собственные частоты цепи) могут быть вычислены относительно просто, степень искажений может быть оценена сравнением длительности импульса с длительностью переходного процесса (необходимо учитывать также форму переходного процесса);
2) в цепях высокого порядка, где вычисление собственных частот затруднительно, сравнивают полосу пропускания цепи (определяемую значительно проще) с шириной спектра сигнала.
В обоих случаях оценка искажений будет приближенной, т.е. качественной:
чем меньше длительность и колебания переходного процесса, тем меньше ожидаются искажения;
если главная часть спектра сигнала лежит в полосе пропускания цепи, то следует ожидать малых искажений.
Исследуемая в работе цепь первого порядка имеет собственную частоту
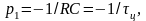
где ц – постоянная времени цепи.
Уменьшение ц уменьшает длительность переходного процесса и искажение сигнала. Очевидно, если ц будет на порядок меньше длительности сигнала, то искажения ожидаются незначительные.
В исследуемой цепи второго порядка собственные частоты определяются выражением
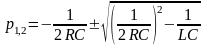 .
.
Наиболее быстрый
переходный процесс и, следовательно,
меньшие искажения формы сигнала будут
при кратных собственных частотах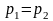 ;
при вещественных различных корнях
длительность переходного процесса
увеличивается, а при комплексных
собственных частотах переходный процесс
становится колебательным и появляются
«выбросы» на переднем и заднем фронтах
выходного сигнала.
;
при вещественных различных корнях
длительность переходного процесса
увеличивается, а при комплексных
собственных частотах переходный процесс
становится колебательным и появляются
«выбросы» на переднем и заднем фронтах
выходного сигнала.
Исследуемые в работе цепи высокого порядка также представляют собой фильтр нижних частот, но для оценки искажений здесь следует использовать частотный подход. АЧХ функции передачи по напряжению
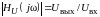
в области малых
частот мало отличается от начального
значения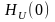 .
Ширина полосы определяется граничной
частотой (частотой среза
.
Ширина полосы определяется граничной
частотой (частотой среза
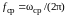 ),
на которой выполняется условие
),
на которой выполняется условие
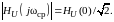
Амплитудный спектр
единичного по уровню входного
прямоугольного импульса длительностью
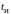 описывается выражением
описывается выражением
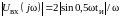 .
.
Ширина спектра определяется в первом приближении шириной первого «лепестка», т. е. первым нулем спектра
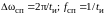 .
.
Очевидно, что искажения будут малы при выполнении условия
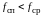 .
.
Обработка результатов:
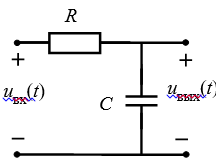
1. Исследование искажений в цепи первого порядка.
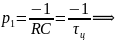
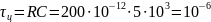
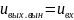
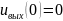
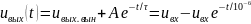
Полоса
пропускания
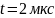 как определили?
Согласно МУ (см. стр 11)
как определили?
Согласно МУ (см. стр 11)



2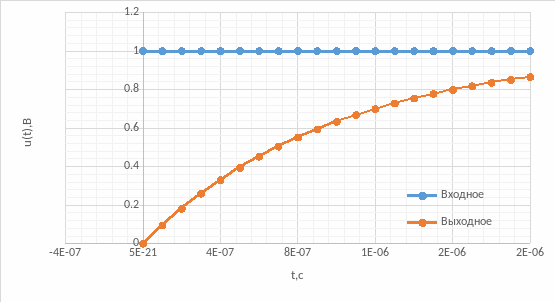 мкс
мкс
1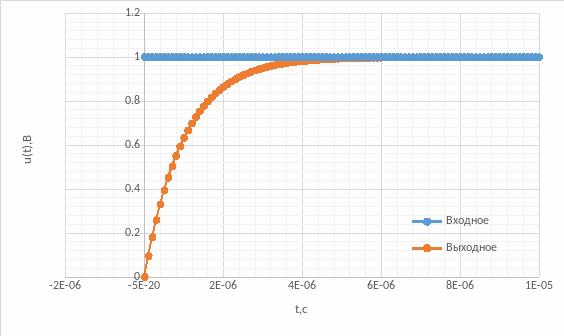 0мкс
0мкс
Полученные экспериментально графики совпадают с полученными в ходе расчётов.
 2.
Исследование искажений в цепи второго
порядка.
2.
Исследование искажений в цепи второго
порядка.
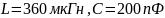
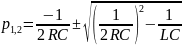
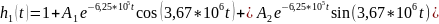
З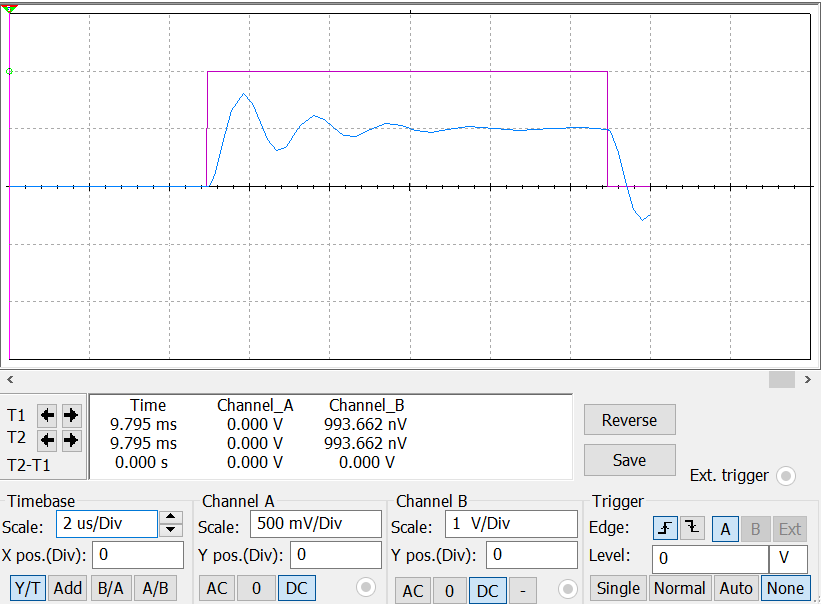 атухающий
колебательный режим
атухающий
колебательный режим

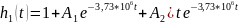
Критический режим

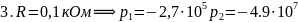
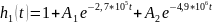
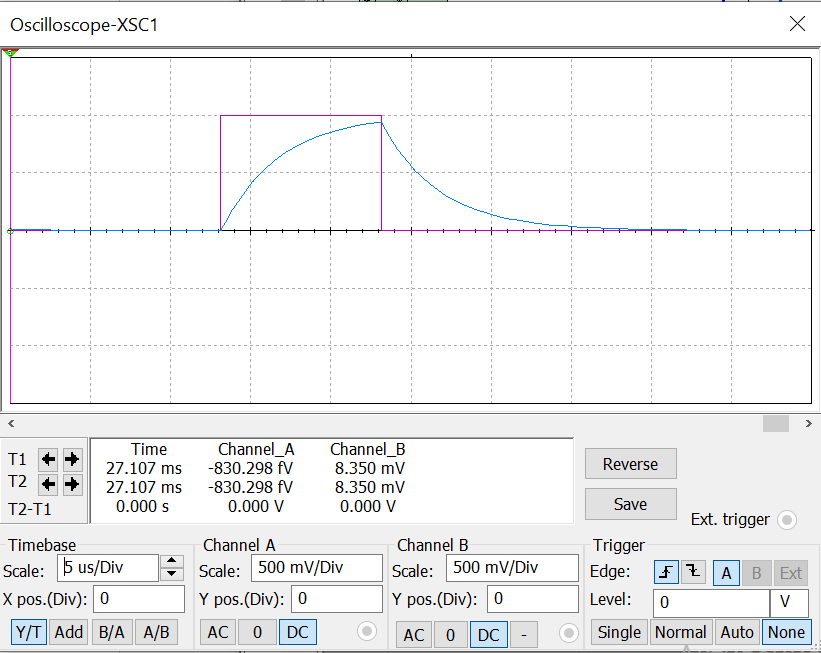
Искажение сигналов объясняется наличием сопротивления
Запишите, согласно МУ, выражения для переходной характеристики цепи в каждом из случаев. (записал согласно МУ)
3. Исследование искажений в цепи высокого порядка.

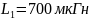
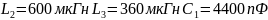
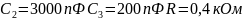
при
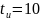 мкс
мкс

при
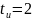 мкс
мкс
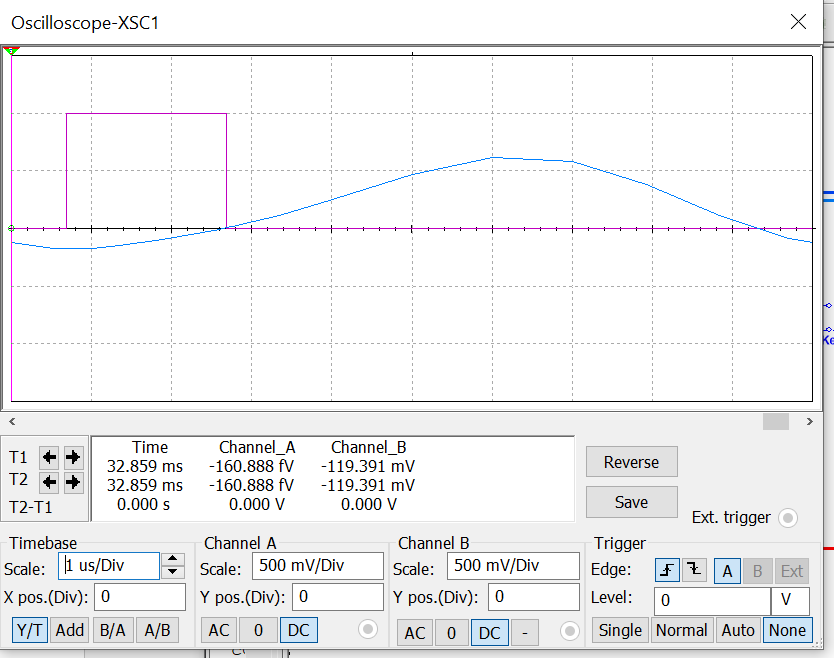
Искажение сигналов объясняется наличием сопротивления.

Постройте графики амплитудных спектров и проведите дальнейшие вычисления согласно МУ.

Определим полосу пропускания цепи:
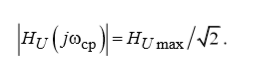
![]()
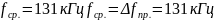

Ширина спектра:
![]()
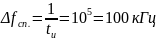 ,
при
мкс
,
при
мкс
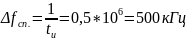 ,
при
мкс
,
при
мкс
Вывод
В этой работе мы изучили характер и степень искажений импульсных сигналов прямоугольной формы при прохождении их через линейные цепи (фильтры нижних частот). Расчетные и экспериментальные данные практически соответствуют. Для оценки искажений используют два основных подхода.
В цепях первого и второго порядков, где корни характеристического уравнения (собственные частоты цепи) могут быть вычислены относительно просто, степень искажений может быть оценена сравнением длительности импульса с длительностью переходного процесса (необходимо учитывать также форму переходного процесса). В цепях высокого порядка, где вычисление собственных частот затруднительно, сравнивают полосу пропускания цепи (определяемую значительно проще) с шириной спектра сигнала. В обоих случаях оценка искажений будет приближённой, т.е. качественной.
Вопросы
Чем объясняются искажения проходящих через цепь сигналов?
Искажения объясняются несовпадением идеальных и реальных характеристик системы, неидеальностью фазо-частотной и амплитудно-частотной характеристик системы обработки и передачи сигнала.
Соответствуют ли расчетные данные экспериментальным и чем объяснить их различие?
Расчетные и экспериментальные данные практически соответствуют. Небольшое различие объясняется тем, что при расчете присутствует округление и тем, что при расчете подразумеваются идеальные элементы: провода без сопротивления, вольтметр с бесконечно большим сопротивлением и т.п. В результате чего отсутствует погрешность, которая наблюдается при эксперименте.
В чем сходство и различие спектральных и частотных характеристик?
Частотные
характеристики цепи
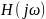 связаны с
передаточной функцией
связаны с
передаточной функцией
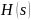 ,
которая является изображением по Лапласу
импульсной характеристики
,
которая является изображением по Лапласу
импульсной характеристики
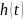 ,
следующей формулой
,
следующей формулой

Поскольку
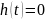 ,
при
,
при
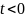 нижний предел в интеграле можно расширить
до
нижний предел в интеграле можно расширить
до
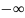 и перейти к двухстороннему преобразованию
Фурье
и перейти к двухстороннему преобразованию
Фурье
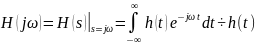
из формулы следует, что частотные характеристики являются спектром импульсной характеристики цепи.
Следствие: все
свойства четности спектральных
характеристик справедливы для частотных
характеристик цепи, т.е.
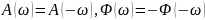 .
.
Различия:
Спектр сигнала – это представление сигнала бесконечной суммой гармоник (синусоид).
Частотные характеристики определяют, как синусоидальные сигналы различных частот «проходят» через цепь в установившимся синусоидальном режиме.