
ЛАБЫ 4 семестр / 8363_NersisyanA_LAB_3_ispravl_4
.docxЧто такое свободный режим и свободная составляющая решения?
Порядок
цепи обычно определяется суммарным
числом имеющихся в ней накопителей,
т.е.
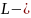 и
и
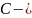 элементов.
Переходные процессы в линейных цепях
возникают при коммутации, т.е. при
переключениях идеального ключа,
изменениях скачком воздействий или их
производных.
элементов.
Переходные процессы в линейных цепях
возникают при коммутации, т.е. при
переключениях идеального ключа,
изменениях скачком воздействий или их
производных.
В
цепях первого порядка переходные
процессы описываются решением линейного
дифференциального уравнения первого
порядка, связывающего реакцию
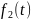 с
воздействием
с
воздействием
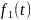 :
:
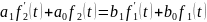
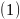
Решение (1) обычно ищут в виде суммы двух составляющих
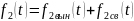
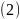
где
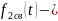 свободная
составляющая
решения (1), т.е. общее решение однородного
дифференциального уравнения
свободная
составляющая
решения (1), т.е. общее решение однородного
дифференциального уравнения
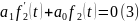
причем
(3) описывает также свободный
режим,
т.е. режим цепи без источников. В свободном
режиме процесс протекает за счет
начальных запасов энергии в накопительных
элементах
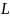 или
или
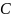 ;
с течением времени эта энергия расходуется
в
;
с течением времени эта энергия расходуется
в
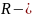 элементах
цепи, поэтому свободный процесс и,
следовательно,
элементах
цепи, поэтому свободный процесс и,
следовательно,
 затухает.
затухает.
В цепях первого порядка свободная составляющая имеет вид
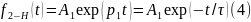
где
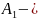 постоянная интегрирования, определяемая
по начальным условиям;
постоянная интегрирования, определяемая
по начальным условиям;
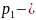 частота собственных колебаний, т.е.
корень характеристического уравнения
частота собственных колебаний, т.е.
корень характеристического уравнения
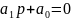 ,
получаемого
из однородного уравнения (3) заменой
,
получаемого
из однородного уравнения (3) заменой
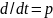 ;
;
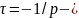 постоянная
времени цепи, измеряемая в секундах.
Для
постоянная
времени цепи, измеряемая в секундах.
Для
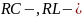 цепей
соответственно
цепей
соответственно
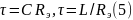
где
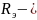 эквивалентное сопротивление цепи в
свободном режиме относительно выводов
накопительного элемента (
или
).
эквивалентное сопротивление цепи в
свободном режиме относительно выводов
накопительного элемента (
или
).
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОЭ
отчет
по лабораторной работе №3
по дисциплине «Теоретические основы электротехники»
Тема: Исследование свободных процессов
в электрических цепях
Студент гр. 8363 |
|
Нерсисян А.С. |
Преподаватель |
|
Константинова Е.В. |
Санкт-Петербург
2020
Цель работы.
Изучение
связи между видом свободного процесса
в электрической цепи и расположением
ее собственных частот (корней
характеристического уравнения) на
комплексной плоскости; экспериментальное
определение собственных частот и
добротности
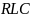 -контура
по осциллограммам.
-контура
по осциллограммам.
Выполнение работы.
Исследование свободных процессов в цепи первого порядка.
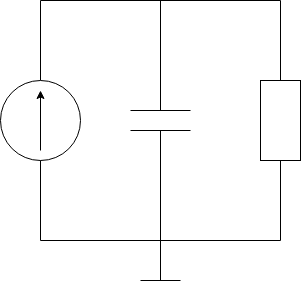
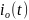
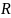
Цепь первого порядка
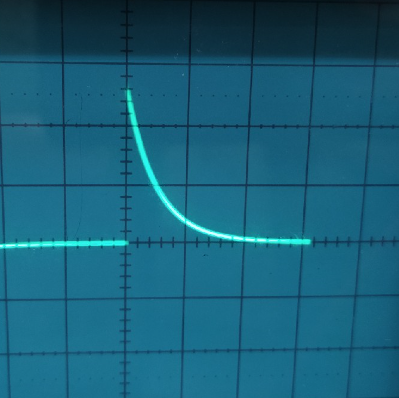
Осциллограмма 1
Исходная цепь (Рис.1) имеет параметры: = 0,02 мкФ, 𝑅 = 5 кОм.
Определение собственной частоты цепи.
Теоретический расчет:
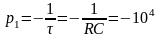 с-1
с-1
Свободный
процесс имеет вид:

Практический расчет:
τ ≈ 0,1 *10-3
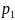 =
=
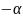 ≈
≈
 (
(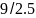 )/(0.15
)/(0.15 10-3)
≈
10-3)
≈
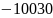 с-1
с-1
Исследование свободных процессов в цепи второго порядка.

Т
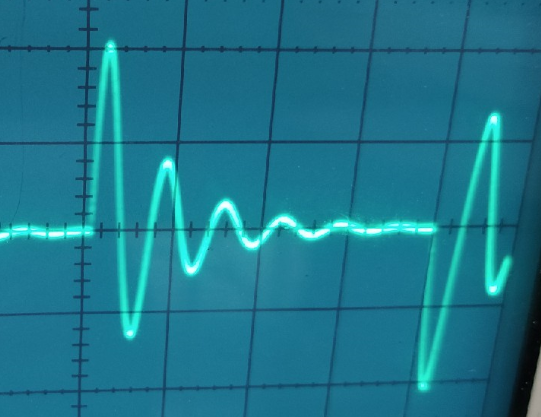
Осциллограмма 2 (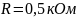 )
)
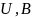
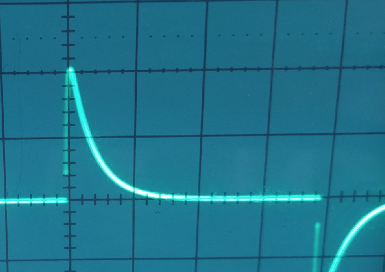 Осциллограмма
3 (
3 кОм)
Осциллограмма
3 (
3 кОм)
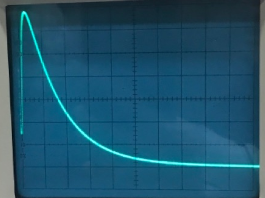
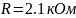 )
)
9 В
8 В
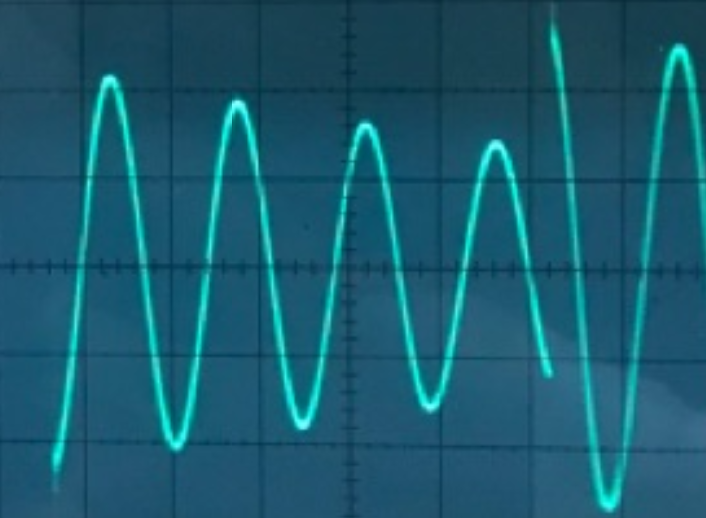 Осциллограмма
5 (
Осциллограмма
5 ( )
)
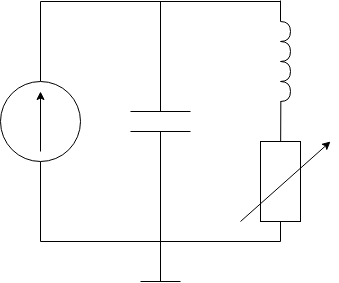
Цепь второго порядка
Исходная
цепь имеет параметры:
𝑅1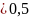 кОм (колебательный режим),
= 0,02 мкФ, 𝐿
кОм (колебательный режим),
= 0,02 мкФ, 𝐿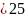 мГн.
мГн.
Теоретический расчет:
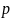 =
−𝛼
±
=
−𝛼
±
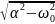
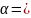 𝑅
2𝐿
𝑅
2𝐿
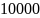
𝜔0
1
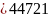
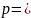 −10000
±
−10000
±
 с-1
с-1
Теоретическая добротность:
𝑄 𝜔0 2𝛼
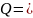 2,236
2,236
Практический
расчет при
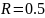 кОм: Укажите
величины на осциллограмме
кОм: Укажите
величины на осциллограмме
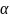
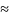
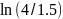 /
/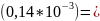 7006
7006
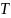
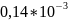 c
𝜔0
c
𝜔0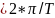 44879
44879
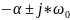 =
=
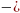 7006
±
7006
±
 44879
с-1
44879
с-1
𝑄 𝜔0 2𝛼
 3,2
3,2
Практический
расчет при
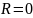 кОм (Незатухающие колебания)
кОм (Незатухающие колебания)
𝑄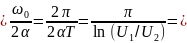
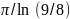
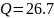
Практический
расчет при
 кОм (Критический режим):
кОм (Критический режим):
Теоретический расчет:
−𝛼
𝛼 𝑅 2𝐿 42000
𝜔0 1 44721
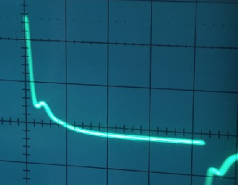
Практический расчет:
−1/tm=33000
И
сследование свободных процессов в цепи третьего порядка.

Цепь третьего порядка
Исходная
цепь (Рис.13)
имеет параметры:
𝑅1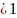 кОм (колебательный режим),
= 0.02 мкФ,
кОм (колебательный режим),
= 0.02 мкФ,
 кОм, 𝐿
мГн.
кОм, 𝐿
мГн.
Теоретический расчет:
1
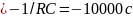 -1
-1
2,3
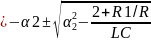
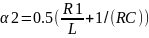
2,3 -1
-1
В общем виде: Уточните запись
𝑈(𝑡)
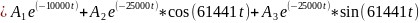
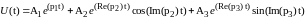 -
начальная формула
-
начальная формула
Вывод.
Форма реакции цепи зависит от вида собственных частот: если собственные частоты вещественные, то апериодический режим, если комплексно-сопряженные, то периодический режим, если кратные, то критический апериодический режим. В данной лабораторной работе изучались не идеальные, а реальные цепи, в следствии чего результаты аналитических расчетов не совпадают с данными осциллограмм. При аналитических расчетах не учитывались неточности схемы и измерительных приборов, сопротивления проводов. Неточность измерений привела в некоторых моментах к несовпадению теоретических и практических результатов обработки данных.
