
- •Двойственная функция.
- •Самодвойственная функция.
- •45. Нормальные алгоритмы Маркова: определение, примеры.
- •46. Определения алгоритма по Тьюрингу, Черчу и Маркову.
- •47. Вычислительная сложность алгоритма: определение. Приведите пример алгоритма, имеющего сложность o(n5).
- •48. Детерминированная и недетерминированная мт. Классы p и np - определение, связь с мт.
- •47. Вычислительная сложность алгоритма: определение. Приведите пример алгоритма, имеющего сложность o(n5).
- •48. Детерминированная и недетерминированная мт. Классы p и np - определение, связь с мт.
- •49. Язык, распознающая грамматика, порождающая грамматика - определения.
Операция дизъюнкция. Логическое сложение, логическое ИЛИ. «или то, или это, или оба сразу» Определение: x+y; СДНФ:
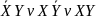 ;
СКНФ: x+y;
ЖИ:
;
СКНФ: x+y;
ЖИ:
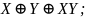 ТИ: (0111).
ТИ: (0111).Операция конъюнкция. Логическое умножение, логическое И.
Определение:
xy;
СДНФ:
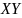 ;
СКНФ:
;
СКНФ: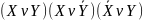 ;
ЖИ:
;
ЖИ:
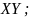 ТИ: (0001).
ТИ: (0001).
Операция импликация. Логическая связка, по своему применению приближенная к союзам «если…, то…». Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно.
Определение:
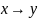 ;
СДНФ:
;
СДНФ:
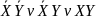 ;
СКНФ:
;
СКНФ: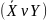 ;
ЖИ:
;
ЖИ:
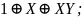 ТИ: (1101).
ТИ: (1101).
Операция эквивалентность. Это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность.
Определение:
 ;
СДНФ:
;
СДНФ:
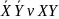 ;
СКНФ:
;
СКНФ: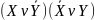 ;
ЖИ:
;
ЖИ:
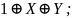 ТИ: (1001).
ТИ: (1001).
Операция исключающее или. Сложение по модулю 2. В случае двух переменных результат выполнения операции является истинным тогда и только тогда, когда один из аргументов является истинным, а второй ложным. Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов, равных 1, составляющих текущий набор, — нечётное.
Определение:
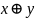 ;
СДНФ:
;
СДНФ:
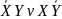 ;
СКНФ:
;
СКНФ: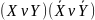 ;
ЖИ:
;
ЖИ:
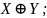 ТИ: (0110).
ТИ: (0110).
Операция отрицание. Логическое НЕ. Операция, результатом которой является суждение (в известном смысле) «противоположное» исходному.
Определение:
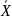 ;
СДНФ:
;
СКНФ:
;
ЖИ:
;
СДНФ:
;
СКНФ:
;
ЖИ:
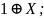 ТИ: (10).
ТИ: (10).
Операция Штрих Шеффера. Таким образом, высказывание
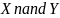 означает, что X и Y несовместны, то есть
не являются истинными одновременно.
означает, что X и Y несовместны, то есть
не являются истинными одновременно.
Определение:
; СДНФ:
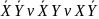 ;
СКНФ:
;
СКНФ: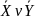 ;
ЖИ:
;
ЖИ:
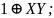 ТИ: (1110).
ТИ: (1110).
Операция стрелка Пирса. Таким образом, высказывание «X ↓ Y» означает «не max (X,Y)». От перемены мест операндов результат операции не изменяется.
Определение: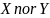 ; СДНФ:
; СДНФ:
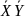 ;
СКНФ:
;
СКНФ: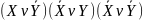 ;
ЖИ:
;
ЖИ:
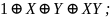 ТИ: (1000).
ТИ: (1000).
СДНФ. Формула
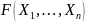 имеет
совершенную дизъюнктивную нормальную
форму (СДНФ), если выполнены следующие
условия: 1) F
имеет ДНФ; 2) каждая элементарная
конъюнкция ДНФ содержит один и только
один из литералов
имеет
совершенную дизъюнктивную нормальную
форму (СДНФ), если выполнены следующие
условия: 1) F
имеет ДНФ; 2) каждая элементарная
конъюнкция ДНФ содержит один и только
один из литералов
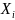 или
или
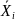 для любого
для любого
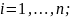 3) F
не содержит одинаковых элементарных
конъюнкций; 4) упорядочена в lex.
Методы построения: 1)
Алгебраические преобразования:
шаг 1) приводим формулу к ДНФ. Шаг 2) Если
в полученной ДНФ какая-то элементарная
конъюнкция С не содержит ни переменной
,
ни ее отрицания для
3) F
не содержит одинаковых элементарных
конъюнкций; 4) упорядочена в lex.
Методы построения: 1)
Алгебраические преобразования:
шаг 1) приводим формулу к ДНФ. Шаг 2) Если
в полученной ДНФ какая-то элементарная
конъюнкция С не содержит ни переменной
,
ни ее отрицания для
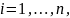 то равносильными преобразованием
заменяем С на две элементарные конъюнкции
то равносильными преобразованием
заменяем С на две элементарные конъюнкции
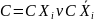 .
Шаг 3) Если элементарная конъюнкция С
содержит два вхождения одного литерала,
то одно из них вычеркиваем. Если же
конъюнкция С содержит
.
Шаг 3) Если элементарная конъюнкция С
содержит два вхождения одного литерала,
то одно из них вычеркиваем. Если же
конъюнкция С содержит
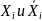 для любого
то
вычеркиваем всю элементарную конъюнкцию.
Шаг 4) Если полученная формула содержит
одинаковые элементарные конъюнкции,
то оставляем одну из них, а остальные
вычеркиваем. 2)
По ТИ:
шаг 1)Составим ТИ формулы
.
Шаг 2) Выделим строки таблицы, в которых
в столбце F
стоит 1. Шаг 3) Каждой выделенной строке
поставим в соответствие элементарную
конъюнкцию. Шаг 4) Составим дизъюнкцию,
определенных на шаге 3 элементарных
конъюнкций. Пример:
для любого
то
вычеркиваем всю элементарную конъюнкцию.
Шаг 4) Если полученная формула содержит
одинаковые элементарные конъюнкции,
то оставляем одну из них, а остальные
вычеркиваем. 2)
По ТИ:
шаг 1)Составим ТИ формулы
.
Шаг 2) Выделим строки таблицы, в которых
в столбце F
стоит 1. Шаг 3) Каждой выделенной строке
поставим в соответствие элементарную
конъюнкцию. Шаг 4) Составим дизъюнкцию,
определенных на шаге 3 элементарных
конъюнкций. Пример:
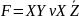 ;
;
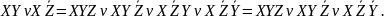
minДНФ. ДНФ называют минимальной, если она содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей ДНФ. Методы построения: 1) метод минимизирующих карт: шаг 1) оставляем только строки, содержащие СЭК, присутствующие в СДНФ; шаг 2) В оставшихся строках вычеркиваем ЭК, которые уже вычеркнуты; шаг 3) В каждой невычеркнутой строке оставляем ЭК только минимальной длины; шаг 4) В каждой невычеркнутой строке выбираем по одной ЭК, составляем таким образом все возможные ДНФ, упрощаем их и выбираем min. 2) Алгебраические преобразования.
Пример:
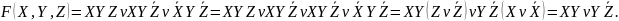 MinДНФ:
MinДНФ:
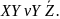
СКНФ. Формула имеет совершенную конъюнктивную нормальную форму (СКНФ), если выполнены следующие условия: 1) F имеет КНФ; 2) каждая ЭД содержит один и только один из литералов или для любого
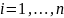 ;
3) F
не содержит одинаковых ЭД. Методы
построения: 1)
Алгебраические преобразования:
шаг 1) Приведем формулу к КНФ. Шаг 2) Если
в полученной на первом шаге КНФ
какая-либо ЭД D
не содержит ни переменной
ни
для
,
то равносильным преобразованием
заменяем D
на две ЭД:
;
3) F
не содержит одинаковых ЭД. Методы
построения: 1)
Алгебраические преобразования:
шаг 1) Приведем формулу к КНФ. Шаг 2) Если
в полученной на первом шаге КНФ
какая-либо ЭД D
не содержит ни переменной
ни
для
,
то равносильным преобразованием
заменяем D
на две ЭД:
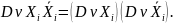 Шаг 3) Если ЭД D
содержит два вхождения одного литерала,
то одно из них вычеркиваем. Если же
дизъюнкции D
содержит
и
для
,
то вычеркиваем всю ЭД. Шаг 4) Если
полученная формула содержит одинаковые
ЭД, то оставляем одну из них, а остальные
вычеркиваем. 2)
По ТИ:
шаг 1)Составим ТИ формулы
.
Шаг 2) Выделяем строки таблицы, в которых
в столбце F
стоит 0. Шаг 3) Каждой выделенной строке
поставим в соответствие ЭД. Шаг 4)
Составим конъюнкцию, определенных на
шаге 3 элементарных дизъюнкций. Пример:
Шаг 3) Если ЭД D
содержит два вхождения одного литерала,
то одно из них вычеркиваем. Если же
дизъюнкции D
содержит
и
для
,
то вычеркиваем всю ЭД. Шаг 4) Если
полученная формула содержит одинаковые
ЭД, то оставляем одну из них, а остальные
вычеркиваем. 2)
По ТИ:
шаг 1)Составим ТИ формулы
.
Шаг 2) Выделяем строки таблицы, в которых
в столбце F
стоит 0. Шаг 3) Каждой выделенной строке
поставим в соответствие ЭД. Шаг 4)
Составим конъюнкцию, определенных на
шаге 3 элементарных дизъюнкций. Пример:
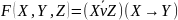 ;
;
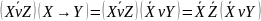 =(
=(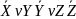 )(X
)(X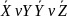 )(
)(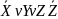 )=(
)=(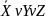 )(
)(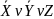 )(
)(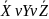 )(
)(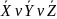 )(X
)(X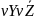 )(X
)(X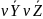 ).
).Полином Жегалкина. Рассмотрим полный класс
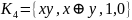 .
Очевидно, что его замыкание содержит
многочлены (от любого числа переменных)
над полем
.
Очевидно, что его замыкание содержит
многочлены (от любого числа переменных)
над полем
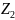 .
Эти многочлены называют полиномами
Жегалкина. Поскольку для элементов
.
Эти многочлены называют полиномами
Жегалкина. Поскольку для элементов
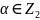 справедливо тождество
справедливо тождество
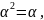 то
полином Жегалкина можно записать в
виде:
то
полином Жегалкина можно записать в
виде:
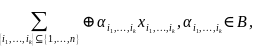 и суммирование ведется по всем
подмножествам множества {1,…,n}.
Методы построения: 1) Алгебраические
преобразования; 2) Методом неопределенных
коэффициентов. Пример:
и суммирование ведется по всем
подмножествам множества {1,…,n}.
Методы построения: 1) Алгебраические
преобразования; 2) Методом неопределенных
коэффициентов. Пример:
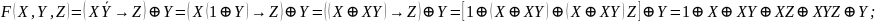
Двойственная функция.
Булева функция f*(x1, …, xn) называется двойственной булевой функции f(x1, …, xn), если она получена из f(x1, …, xn) инверсией всех аргументов и самой функции, то есть
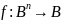
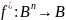
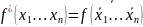
Пример:
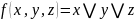
По опр
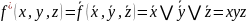
По теор
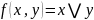
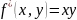
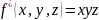
Теорема о построении двойственной функции от суперпозиции. Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций.
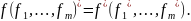
Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций.
По опр
По теор
Для
Самодвойственная функция.
Самодвойственная функция — булева функция, двойственная сама к себе.
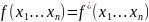
Критерий: У самодвойственной функции ТИ кососимметрична (на симметричных местах противоположные значения)
Достаточное условие НЕсамодвойственности булевой функции. Если число единиц в столбце значений функции не совпадает с числом нулей, то функция не является самодвойственной.
Примеры:
Не самодвойственная
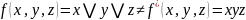
Самодвойственная
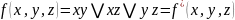
Выводимость: определение. Приведите пример пары высказываний и третьего, выводимого из них, выводимость обоснуйте.
Определение
(выводимость):
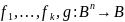 ;
;
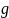 -
логическое следствие
-
логическое следствие
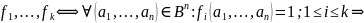
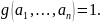 Обозначение:
Обозначение:
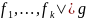 .
.
Другое
определение:
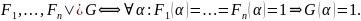
Пример:
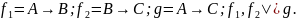 Доказать построением ТИ.
Доказать построением ТИ.
Выполнимость: определение. Приведите примеры выполнимого и невыполнимого наборов высказываний, ответ обоснуйте.
Набор
функций
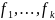 называют выполнимым:
называют выполнимым:
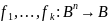 выполнимый
выполнимый
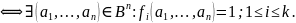
Проверить
выполнимость множества формул (например
F1,F2,F3)
можно построением совместной таблицы
истинности этих формул. Если найдется
хотя бы одна строка, в которой в столбцах
формул (F1,
F2, F3) стоят единицы, то это множество
выполнимо. Если такой строки нет, то
множество формул невыполнимо. Выполнимо: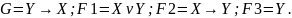 Для невыполнимого аналогично построить,
только с наличием нулей в строках
функций.
Для невыполнимого аналогично построить,
только с наличием нулей в строках
функций.
Резольвента: определение. Связь резольвенты и выводимости. Приведите пример набора высказываний, для которого множество всех возможных резольвент состоит из не менее четырех различных элементов.
Дизъюнкт
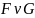 называют резольвентой дизъюнктов
называют резольвентой дизъюнктов
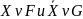 .
Пусть
D1=B1vA
, D2=B2v¬A
- дизъюнкты. Дизъюнкт B1vB2 называется
резольвентой дизъюнктов D1 и
D2 по
литере А и обозначается через resA(D1,D2).
.
Пусть
D1=B1vA
, D2=B2v¬A
- дизъюнкты. Дизъюнкт B1vB2 называется
резольвентой дизъюнктов D1 и
D2 по
литере А и обозначается через resA(D1,D2).
Резольвента является логическим следствием порождающих ее дизъюнктов.
Пример:
множество дизъюнктов
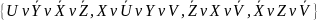 .
Пример резольвенты
Res=
.
Пример резольвенты
Res=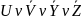 .
.
К каким задачам применим метод резолюций в логике высказываний? Алгоритм решения задачи методом резолюций.
?Особенность метода состоит в том, что он оперирует не с произвольными формулами, а с дизъюнктами.
Алгоритм:
Шаг1) Составляем множество формул
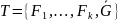 .
Шаг2) Каждую из формул множества Т
приводим к КНФ. Шаг3) Разбираем КНФ на
элементарные дизъюнкты. Шаг4) Строим
все возможные резольвенты набора ЭД,
полученного в 3 пункте.
.
Шаг2) Каждую из формул множества Т
приводим к КНФ. Шаг3) Разбираем КНФ на
элементарные дизъюнкты. Шаг4) Строим
все возможные резольвенты набора ЭД,
полученного в 3 пункте.
Приведите пример решения задачи логики высказываний методом резолюций.
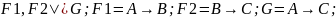 Шаг1)
Шаг1)
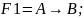
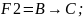
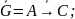 Шаг2)
Шаг2)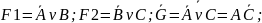
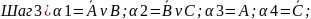 Шаг4)
Res(
Шаг4)
Res(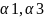 )=B:=
)=B:=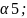 Res(
Res(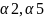 )=C:=
)=C:=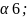 Res(
Res(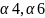 )=0.
)=0.
Замкнутость множества относительно операции: определение, примеры.
Если над двумя элементами одного множества выполняется какая-либо арифметическая(бинарная) операция, и полученный результат также принадлежит этому множеству, то говорится, что это множество замкнуто относительно данной операции.
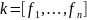 – все
булевы функции, обладающие свойством
– все
булевы функции, обладающие свойством
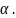 k-класс
замкнутости булевых функций относительно
свойства
k-класс
замкнутости булевых функций относительно
свойства
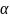 ,
если любая композиция функций из k
лежит в k.
,
если любая композиция функций из k
лежит в k.
?Пример:
если
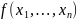 сохраняет 0 и
сохраняет 0 и
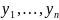 -новые
переменные, то очевидно что
-новые
переменные, то очевидно что
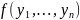 также сохраняет ноль. Это означает, что
класс T0
замкнут относительно операции
переименования переменных. Пусть
также сохраняет ноль. Это означает, что
класс T0
замкнут относительно операции
переименования переменных. Пусть
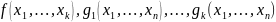 сохраняет 0. Тогда
сохраняет 0. Тогда
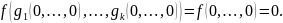 Это означает, что T0
замкнут относительно операции
подстановки. Следовательно, замкнутый
класс.
Это означает, что T0
замкнут относительно операции
подстановки. Следовательно, замкнутый
класс.
Класс замкнутости T0: определение. Примеры функций, принадлежащих и не принадлежащих классу T0 . Критерий принадлежности классу T0 в терминах полинома Жегалкина.
Функцию
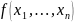 называют сохраняющей ноль, если
называют сохраняющей ноль, если
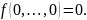 Через T0
обозначим класс всех функций, сохраняющих
0, т.е.
Через T0
обозначим класс всех функций, сохраняющих
0, т.е.
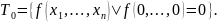
Пример:
принадлежит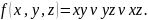 Критерий принадлежности классу T0
в терминах полинома Жегалкина: коэффициент
при свободном члене равен нулю.
Критерий принадлежности классу T0
в терминах полинома Жегалкина: коэффициент
при свободном члене равен нулю.
Класс замкнутости T1: определение. Примеры функций, принадлежащих и не принадлежащих классу T1 . Критерий принадлежности классу T1 в терминах полинома Жегалкина.
Функцию
называют сохраняющей единицу, если
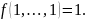 Через T1
обозначим класс всех функций, сохраняющих
1, т.е.
Через T1
обозначим класс всех функций, сохраняющих
1, т.е.
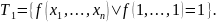
Пример: принадлежит Критерий принадлежности классу T1 в терминах полинома Жегалкина: полином Жегалкина имеет нечетное число слагаемых.
Класс замкнутости L: определение. Примеры функций, принадлежащих и не принадлежащих классу L.
Функцию
называют линейной, если она представима
в виде линейного полинома Жегалкина,
т.е. если существуют
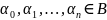 такие, что
такие, что
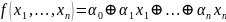 .
.
Пример:
принадлежит
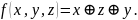 Не принадлежит
Не принадлежит
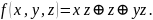
Класс замкнутости S: определение. Примеры функций, принадлежащих и не принадлежащих классу S. Критерий принадлежности классу S в терминах ТИ.
Булеву
функцию
называют самодвойственной, если
выполняется равенство
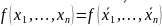 .
Другими словами, функция самодвойственна,
если она совпадает со своей двойственной.
Критерий принадлежности классу S
в терминах ТИ: При лексикографическом
упорядочивании строк таблицы значений
самодвойтвенной функции последний
столбец (значения функции) антисимметричен
относительно середины таблицы. Пример:
не принадлежит
.
Другими словами, функция самодвойственна,
если она совпадает со своей двойственной.
Критерий принадлежности классу S
в терминах ТИ: При лексикографическом
упорядочивании строк таблицы значений
самодвойтвенной функции последний
столбец (значения функции) антисимметричен
относительно середины таблицы. Пример:
не принадлежит
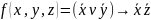 .
Принадлежит
.
Принадлежит
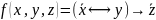 .
.
Понятие сравнимых наборов аргументов для булевой функции. Приведите примеры пары сравнимых и несравнимых наборов аргументов. Является ли соответствующий порядок частичным, линейным, полным? Ответ обоснуйте.
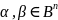
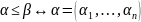 ;
;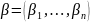 ;
;
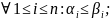
Определение:
Будем говорить, что набор
не превосходит набор
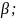
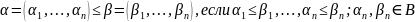 .
Наборы
.
Наборы
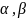 называются сравнимыми, если
называются сравнимыми, если
 ;
в противном случае они называются
несравнимыми. Примеры: сравнимые
(0,1,0,0) и (1,1,0,1); не сравнимы (0,1,0,0) и
(1,0,0,1).
;
в противном случае они называются
несравнимыми. Примеры: сравнимые
(0,1,0,0) и (1,1,0,1); не сравнимы (0,1,0,0) и
(1,0,0,1).
Частичный
порядок: рефлексивно
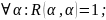 антисимметрично
антисимметрично
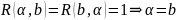 ;
транзитивно
;
транзитивно
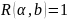
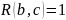
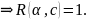 Линейный порядок – частичный порядок
с доп. условием, хоть одно из
Линейный порядок – частичный порядок
с доп. условием, хоть одно из
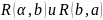 для
любых
для
любых
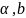 ,
равно единице.
,
равно единице.
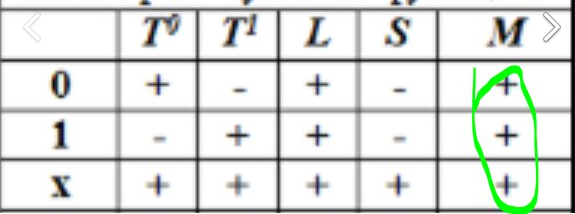
Класс замкнутости M: определение. Примеры функций, принадлежащих и не принадлежащих классу M. Какую информацию о принадлежности классу M можно получить, анализируя принадлежность функции классам
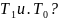
Булеву
функцию
называют монотонной, если для любых
двух наборов
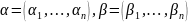 из условия
из условия
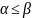 следует, что
следует, что
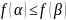 .
.
Пример:
не монотонна
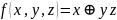 .
Монотонна
.
Монотонна
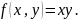 Рассматривая классы
Рассматривая классы
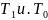 ,
мы определяем крайние значения функции,
тем самым в некоторых случаях можно
сразу определить монотонность.
,
мы определяем крайние значения функции,
тем самым в некоторых случаях можно
сразу определить монотонность.
Полная система булевых функций: определение. Приведите примеры полной и неполной систем, состоящих их трех функций каждая. Ответ обоснуйте.
Класс булевых функций K является полным тогда и только тогда, когда он не содержится ни в одном из основных замкнутых классов.
Примеры:
полная система:
 Неполная система:
Неполная система:
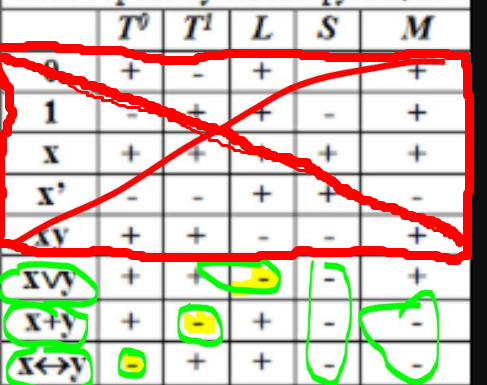
Критерий полноты системы булевых функций. Каково минимально возможное количество функций в полной системе? Приведите пример, обоснуйте.
Необходимый и достаточный критерий полноты класса булевых функций, это и есть теорема Поста: Класс булевых функций K является полным тогда и только тогда, когда он не содержится ни в одном из основных замкнутых классов.
Минимально возможное количество функций в полной системе:1. X nor Y и X nand Y – полные системы.
Теорема Поста. Может ли полная система содержать более трех функций, так, чтобы ни одну из них нельзя было исключить? Приведите пример или докажите, что это невозможно.
Теорема Поста: Класс булевых функций K является полным тогда и только тогда, когда он не содержится ни в одном из основных замкнутых классов.
Теорема
о максимальном числе функций в базисе:
максимально возможное число булевых
функций в базисе — четыре. Во
всяком базисе F содержится
не более 4-х функций. Пример:
 .
.
31) Шифр Вернама. Определение, криптоустойчивость. Примеры шифровки и дешифровки при помощи шифра Вернама.
Шифра Вернама – система симметричного шифрования, изобретенная в 1917 году. Обладает абсолютной криптографической стойкостью, т. е. противостоит криптоанализу.
Сообщение – a
k – ключ, такой же длины, как и сообщение.
Шифровка: сообщение объединяется с операцией исключающее ИЛИ с секретным ключом.
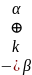
Дешифровка: зашифрованное сообщение объединяется с операцией исключающее ИЛИ с секретным ключом.
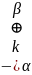
Пример:
шифровка: (11000)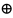 (11101) = (00101)
(11101) = (00101)
дешифровка: (00101) (11101) = (11000)
32) Разложение Шеннона: определение, примеры. Связь с бинарными диаграммами решений.
Разложение Шеннона – метод представления булевой функции от n переменных в виде суммы двух подфункций от (n-1) остальных переменных.
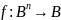 ,
,
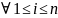
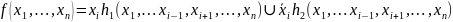
Пример:
f(x,y,z)=x+y+z=x(1+y+z) +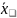 (0+y+z)
(0+y+z)
34) Определение предиката. Связанная и свободная переменная. Приведите примеры формул в логике предикатов, иллюстрирующие фактическое изменение количества переменных при навешивании кванторов.
Предикат – функция, определенная на некотором множестве параметров и со значениями в {0,1}.
Переменную называют свободной, если существует хотя бы одно свободное вхождение переменной в формулу и связной, если имеется связное вхождение. Вхождение называют связанным, если переменная стоит непосредственно за квантором или входит в область действия квантора по этой переменной.
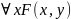 x
– связанная переменная, y
– свободная.
x
– связанная переменная, y
– свободная.
Пример:
F(x)
– х переменная,
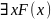 x
– константа.(хз правильный ли пример)
x
– константа.(хз правильный ли пример)
35) Тождества логики предикатов для формул, содержащие связанные переменные: отрицание и замена переменной.
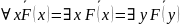
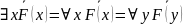
36) Тождества логики предикатов для формул, содержащие связанные переменные: вынесение квантора всеобщности из конъюнкции и дизъюнкции.
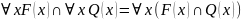
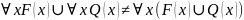
37) Тождества логики предикатов для формул, содержащие связанные переменные: вынесение квантора существования из конъюнкции и дизъюнкции.
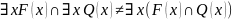
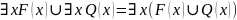
38) Тождества логики предикатов для формул, содержащие связанные переменные: перестановка связанных переменных.
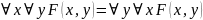
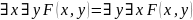
39) Предваренная нормальная форма: определение. Примеры формул, находящихся и не находящихся в ПНФ. Приведите пример формулы, для которой ПНФ и СНФ имеют разное количество связанных переменных. Обосновать.
Формула имеет ПНФ, если все кванторы вынесены в начало.
Пример:
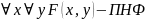
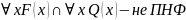
Пример:
ПНФ -
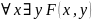 ,
СНФ -
,
СНФ -
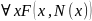 У ПНФ 2 связанные переменные, у СНФ одна.
У ПНФ 2 связанные переменные, у СНФ одна.
40) Сколемовская нормальная форма: определение. Примеры формул, находящихся и не находящихся в СНФ. Приведите пример формулы, для которой ПНФ и СНФ имеют одинаковое количество связанных переменных. Обосновать.
Формула имеет СНФ, если она в ПНФ, матрица в КНФ и нет кванторов существования.
Пример:
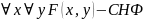
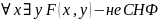
Пример:
ПНФ -
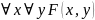 ,
СНФ -
,
СНФ -
41) Унификация и НОУ – определения. Приведите пример пары формул, требующих унификации, укажите их НОУ (не менее трех подстановок)
Пусть
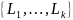 – множество литералов. Подстановку
– множество литералов. Подстановку
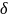 называют унификатором этого множества,
если выполнено равенство
называют унификатором этого множества,
если выполнено равенство
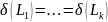 .
Множество называют унифицируемым, если
существует унификатор этого множества.
.
Множество называют унифицируемым, если
существует унификатор этого множества.
Унификатор
множества литералов называют наиболее
общим унификатором этого множества,
если для любого унификатора
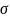 того же множества существует подстановка
того же множества существует подстановка
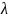 ,
такая что
,
такая что
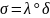
Пример: P(x,y,k(c)) P(f(a),g(b),z)
НОУ = {x=f(a),y=g(b),z=k(c)}
42-44. МТ - определение. Стандартная МТ.
Машина Тьюринга — это строгое математическое построение, математический аппарат, созданный для решения определенных задач, всякий интуитивный алгоритм может быть реализован с помощью нее
Состоит из:
1) Ленты, разбитой на ячейки и бесконечной в обе стороны.
2) Управляющего устройства, которое может находиться в одном из конечного числа внутренних состояний
3) Считывающей/пишущей головки, которая может перемещаться вдоль ленты и в каждый момент времени обозревает (считывает) одну из ячеек ленты.
Функционирование:
А) записывает в эту ячейку символ внешнего алфавита;
Б) сдвигает считывающую головку на один шаг влево или один шаг вправо или оставляет ее на месте;
С) переходит в новое внутреннее состояние.
Таким образом, работа машины определяется системой Команд Вида
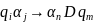
Где 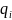 —
внутреннее состояние машины;
—
внутреннее состояние машины; 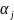 —
считываемый символ;
—
считываемый символ; 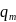 —
новое внутреннее состояние;
—
новое внутреннее состояние; 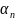 —
новый записываемый символ; D —
направление движения головки, обозначаемой
одним из символов L (влево), R (вправо), Е (на
месте).
—
новый записываемый символ; D —
направление движения головки, обозначаемой
одним из символов L (влево), R (вправо), Е (на
месте).
Пример МТ, реализующей композицию двух МТ.
Сложение двух чисел (2 и 4)
1)q11 -> q2R 4) q31 -> q31R
2) q2 -> q0R 5) q3 -> q41L
q1 – начальное состояние; 6) q41 -> q41L
3) q21 -> q3R 7) q4 -> qfS
qf – конечное состояние;
Пример МТ, реализующей ветвление.
 -MT
генерирующие функции
-MT
генерирующие функции
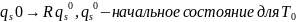
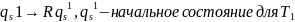
…
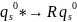
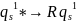
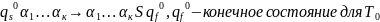
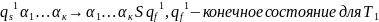
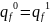
Пример МТ, реализующей цикл.
