ИДЗ-1 МЛиТА
.docx
Группа
8363 Нерсисян
Артур
Математическая логика и теория алгоритмов
Дана
функция
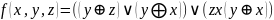
Постройте таблицу истинности для
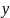
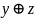
0
0
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
1
1
0
1
0
1
1
0
1
0
1
1
0
0
0
1
0
1
1
0
1
1
1
1
1
1
1
0
1
0
0
1
1
1
1
0
0
0
0
Постройте для композиции
ТИ
и формулу, сделав подстановку в исходную
и упростив ее с помощью алгебраических
преобразований до ДНФ. Убедитесь, что
ответы совпадают.
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
по
ТИ
ДНФ
для
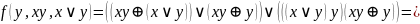
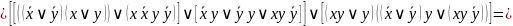
Постройте СДНФ для двумя способами: при помощи ТИ и при помощи АП исходной формулы.
по
ТИ
СДНФ
для
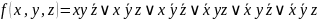
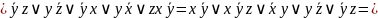
Постройте
минимальную ДНФ
для
методом
минимизирующих карт.
min
ДНФ
для
Постройте СКНФ для двумя способами: при помощи ТИ и при помощи АП исходной формулы.
Пo
ТИ
СКНФ
для
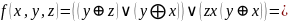
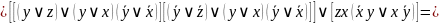
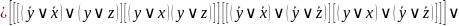
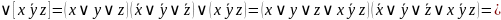
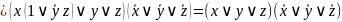
Постройте полином Жегалкина для двумя способами: методом неопределенных коэффициентов и при помощи АП исходной формулы.
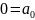
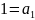
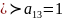
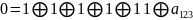
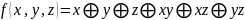
Постройте ТИ для
.
|
|
|
|
|
|
|
|
|
|
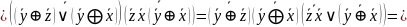
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Постройте полином Жегалкина для любым способом.
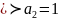
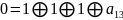
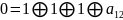
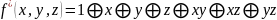
Проверьте полноту системы булевых функций и .
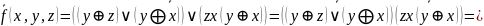
а.
Для
-
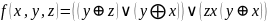
т.к.
т.к.
т.к. число
и
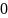не совпадает.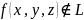
т.к.
,
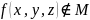
т.к. существует сравнимая пара
т.ч.
при
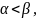
Например, пара
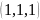и
,
т.к
,
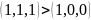
б.
Для
-
т.к.
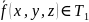
т.к.
т.к. число и не совпадает.
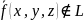
т.к.
,
т.к. существует сравнимая пара т.ч. при
Например, пара
и
,
т.к
,
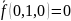
Выразите при помощи композиции функций из предыдущего пункта:
.
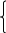
констатнты:
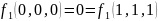
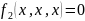
отрицание:
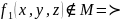существует
сравнимая пара
т.ч.
при
пара
и
следовательно: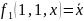
конъюнкция:
|
|
,
,
,
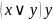
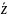
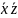
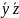
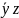
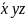
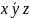
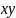
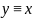
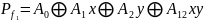
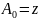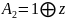