РОСЖЕЛДОР

Государственное образовательное учреждение

высшего профессионального образования

«Ростовский государственный университет путей сообщения»

(РГУПС)

Н.Ф. Добрынин

ЦИКЛ ЛАБОРАТОРНЫХ РАБОТ ПО ГЕОДЕЗИИ

Ростов-на-Дону

2007

УДК 528.4 (075.8)

Добрынин, Н.Ф.

Цикл лабораторных работ по геодезии (4 семестр) для студентов специальности «Земельный кадастр» / Н. Ф. Добрынин; Рост. гос. ун-т путей сообщения. – Ростов н/Д, 2007. – 21 с.: ил.

Изложены задания и методические указания к лабораторным работам по геодезии, посвящённым вычислительной обработке материалов полевых геодезических измерений для определения координат пунктов по различным видам засечек. Две лабораторные работы касаются изучения электронно-оптических средств угловых и линейных измерений.

Для студентов 2-го курса специальности 120302 – Земельный кадастр.

Рецензент: д-р техн. наук, проф. В. И. Куштин (РГСУ)

Учебное издание

Добрынин Николай Федорович

Цикл лабораторных работ по геодезии

Редактор Т. М. Чеснокова

Корректор Т. М. Чеснокова

Подписано в печать 28.12.2007. Формат 60х84/16.

Бумага газетная. Ризография. Усл. печ. л. 1,2.

Уч.-изд. л. 1,3. Тираж 100 экз. Изд. № 59. Заказ № .

Ростовский государственный университет путей сообщения.

Ризография РГУПС.

Адрес университета: 344038, Ростов н/Д, пл. им. Ростовского Стрелкового Полка Народного Ополчения, 2.

© Ростовский государственный университет путей сообщения, 2007

Содержание

Лабораторная работа № 1 Сгущение плотности съемочного обоснования дополнительными точками

А. ПРЯМАЯ УГЛОВАЯ ЗАСЕЧКА

Б. ЛИНЕЙНАЯ ЗАСЕЧКА

В. КОНТРОЛЬНЫЕ ВОПРОСЫ К ЗАЩИТЕ ЛАБОРАТОРНОЙ РАБОТЫ

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА (РГР) ОБРАТНАЯ ЗАСЕЧКА (ЗАДАЧА ПОТЕНОТА)

Лабораторная работа № 2. Точные теодолиты

Лабораторная работа № 3. Электронно-оптические средства линейных измерений

Приложение 1

Приложение 2

Приложение 3

Приложение 4

Приложение 5

Приложение 6

Приложение 7

Лабораторная работа № 1 Сгущение плотности съемочного обоснования дополнительными точками

Исходные материалы:

а) результаты полевых измерений (по вариантам); точность угловых измерений ;

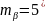б) формуляры (бланки) для вычислений;

в) калькуляторы.

А. Прямая угловая засечка

СОДЕРЖАНИЕ ЗАДАНИЯ

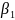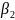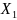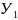На местности (рис. 1) для определения планового положения точки Р теодолитом 2Т5К измерены горизонтальные углы и с вершинами в пунктах А и В, имеющих координаты , и 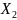, 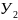. Необходимо определить координаты точки Р ( , ).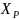

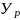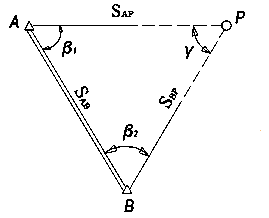
Рис. 1. Прямая угловая засечка

1 Рабочие формулы

Формулы Гаусса

,

Где

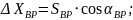
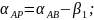
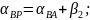
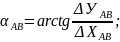
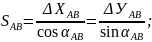
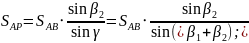
Формулы Юнга:

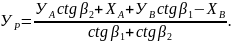
Средняя квадратическая ошибка положения точки Р, обусловленная погрешностями измерения горизонтальных углов и , определяется по следующей формуле:

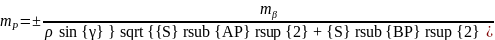
2 Порядок выполнения работы

(Методические указания)

а) координаты исходных (твердых) пунктов даны в приложении 5 (согласно порядковому номеру фамилии студента в журнале группы) с точностью до сотых долей метра и содержат шесть значащих цифр, а углы и измерены до целых секунд. Поэтому во всех промежуточных результатах вычислений удерживать на одну значащую цифру больше, а в угловых величинах – оставлять десятые доли секунды.

б) вычисление координат определяемой точки Р удобнее осуществлять в специальных таблицах (бланках), в которых расписаны приведенные выше формулы, а порядковые номера строк указывают на последовательность вычислительных действий.

в) приращения координат ∆Х, ∆У необходимо сопровождать знаками («+» или «-»).

г) при вычислении дирекционного угла твердой стороны АВ (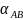 ) сначала получить абсолютную величину румба (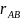 ) по абсолютной величине ∆У_АВ/∆Х_АВ, затем, используя знаки числителя и знаменателя определить его название, а по нему – (приложение 1, строки 7–9).

д) окончательные значения координат определяемого пункта (строки 35 и 36) округлить до двух десятичных знаков.

е) вычисленные в таблице 1 значения S_АР и S_ВР сравнить с их величинами, находящимися в строках 22 и 21; расхождения не должны превышать 3 – 5 единиц в последнем десятичном знаке.

ж) вычислить координаты этой же точки по формулам Юнга (приложение 2).

Б. Линейная засечка

СОДЕРЖАНИЕ ЗАДАНИЯ

На местности (рис. 2) для определения планового положения точки Р светодальномером СТ-5 «Блеск» измерены расстояния и вычислены горизонтальные проложения 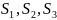соответственно с пунктов государственной геодезической сети А, В, С, координаты которых 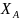, , , , , 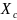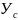известны.

Необходимо определить координаты точки Р( ).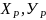

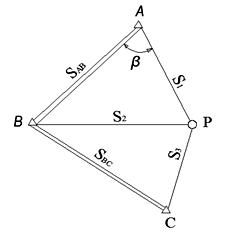
Рис. 2. Линейная засечка

1 Рабочие формулы

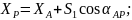
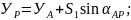
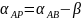( – из решения обратной геодезической задачи);

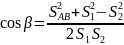(по теореме косинусов).

2 Порядок выполнения работы

В специальную ведомость, образец которой приведен в приложении 3, выписать (по номеру варианта – порядковому номеру фамилии студента в журнале группы) необходимые исходные данные, помещенные в приложении 6.

В ведомости расписаны приведенные выше формулы линейной засечки для двукратного определения планового положения пункта Р по результатам независимых линейных измерений расстояний до него с твердых пунктов А, В и С (S₁, S₂ и S₃). При этом сначала решение задачи осуществляется по длинам линий S₁ и S₂ (левая группа формул в ведомости вычислений), а затем, для контроля вычислительной обработки и оценки точности, используются S₂ и S₃ (правая группа формул).

Промежуточный контроль (контроль вычислений) производится в процессе реализации алгоритма вычислений и заключается в повторном определении уже вычисленных значений некоторых промежуточных результатов по другим параметрам (формулам). Такие действия предусмотрены пунктами 13(к) и 31(к). В первом случае дважды вычисляется величина 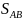(см. п. 12), во втором – 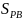, которая соответствует измеренному значению S₂. Расхождения вызваны только округлением промежуточных операций, поэтому не должны превышать двух, реже трех единиц в последнем десятичном знаке.

Заключительный контроль и оценка точности окончательного результата (средняя квадратическая ошибка положения в плане определяемого пункта Р) производится по двум показателям. Первый показатель характеризует качество и точность линейных измерений, погрешности которых неизбежно приведут к разным результатам в координатах определяемого пункта Р, так как в вычислениях использовались разные по величине и ошибкам длины линий (только S₂ использовалась в обоих вариантах вычислительной обработки линейных измерений). Для анализа обычно используют абсолютную ошибку в положении определяемого пункта, вычисляемую по формуле

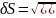
Величина вызвана и зависит от инструментальной точности используемого средства линейных измерений, которое, в свою очередь, выбирается исходя из требуемой точности планового положения определяемого пункта, зависящей не только от использованного прибора, но и от точности координат исходных (твердых) пунктов, с которых выполнены линейные измерения.

Для определения допустимого значения будем полагать, что пункт Р в дальнейшем будет использован для создания планового съемочного обоснования при картографировании территории в масштабе 1:5000. Тогда, согласно инструкции по топографическим съемкам в крупных масштабах, величина не должна превышать 0,15 мм на плане заданного масштаба съемки.

При допустимой величине за окончательное местоположение пункта Р принимают среднее арифметическое из его координат, полученных из двукратного их определения ( и ; и ).

Для оценки точности координат определяемого пункта необходимо сначала вычислить углы γ и γ' (точнее – 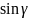и 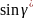) при пункте Р, так как и их величина влияет на точность решения линейной засечки. Непосредственно по схеме засечки (рис. 2) следует (по теореме синусов):

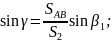
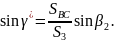
Инструментальная точность СТ-5

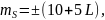
где в мм, а L – длина линии в км.

Таким образом, средняя квадратическая ошибка

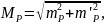
где средние квадратические ошибки первого и второго решени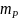й ( и 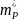), вычисляемые по следующим формулам:

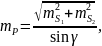
Выполнив указанные вычисления, сделать по ним соответствующие выводы: согласуются ли полученные оценочные величины с требуемыми допусками (с 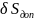по первому критерию) и какова точность окончательного результата ( ).