Специально для групп С-12 / Общая физика_под ред. Белокопытова_2016 -506с

X

x0

наты станет равна: x = v t = px0 t / m.

Теперь, воспользовавшись принципом неопределенности (30.7), получим:

электрон был локализован в области, имеющей размеры атома x0 = = 10– 10 м. Какова же будет неопределенность координаты через 1 с?

Итак, свободная частица, локализованная на размерах атома, за 1 с «расплывется» до расстояний 7000 км!

30.6.Статистический смысл волн де Бройля

В§ 30.5 мы выяснили, что волновой пакет, соответствующий частице, очень быстро расплывается. Возникает вопрос: как интерпретировать волну де Бройля?

Когда квантовая механика только создавалась, существовали различные интерпретации волны де Бройля. В частности, считалось, что частицы представляют собой суперпозицию волн, а интенсивность волн пропорциональна плотности среды, из которой образована частица.

491

Пример 30.9. Вернемся к расчету, выполненному в примере 30.8. Мы видели, что за одну секунду частица «расплывается» до расстояний 7000 км. Если бы интенсивность волны зависела от плотности частицы, то мы могли бы одновременно найти часть электрона в Москве и часть, скажем, в Лондоне. Но это противоречит опыту, который свидетельствует о том, что электрон неделим, т.е. мы можем обнаружить только целый электрон, но никак не его часть. Следовательно, такая интерпретация волн де Бройля нас не устраивает.

В § 30.5 мы рассмотрели интерференцию электронов на двух щелях (рис. 30.9, 30.10). Для характеристики интерференции мы ввели плотность вероятности обнаружения электрона в той или иной области экрана. Итак, свяжем волну де Бройля с плотностью вероятности обнаружения частицы. Для этого сравним наш опыт по интерференции электронов с аналогичным опытом по интерференции света. В этом случае рассматривают интенсивность света, а не плотность вероятности. Выведем формулу для интенсивности при интерференции света от двух когерентных источников.

Рассмотрим две плоские волны, разность фаз которых Δϕ:

Воспользуемся формулой Эйлера

eix = cos x + i sin x.

Теперь вместо формул (30.16) будем писать:

где A — коэффициент пропорциональности.

Используя формулы (30.17) и (30.18), находим интенсивность света при интерференции:

492

Отсюда

I = I1 + I2 + 2I1I2 cos( ϕ) .

Аналогичная ситуация возникает при интерференции электронов, но вместо интенсивности мы рассматриваем плотности вероятности.

Таким образом, плотность вероятности обнаружить частицу в той или иной области пространства связана с волновой функцией. По

аналогии с оптикой для плотности вероятности получим ρ = |ψ|2, где ψ — волновая функция частицы. Тогда вероятность обнаружить частицу в объеме V можно найти по формуле:

Предположим, что частица не взаимодействует с окружением. Тогда, по аналогии с формулами (30.17) будем иметь:

Эта формула соответствует бесконечной монохроматической волне де Бройля. Для волнового пакета соответственно получим:

Для определение константы С воспользуемся следующим свойством вероятности.

Обнаружение частицы в любой точке пространства есть достовер-

Условие (30.21) называется условием нормировки.

Подставляя сюда волновую функцию для монохроматической волны (30.21), получаем:

P = ∫ C 2dV = C 2∫dV = 1 .

Отсюда C = 1⁄ V , где V — объем, стремящийся к бесконечности.

30.7.Некоторые задачи квантовой механики

Вклассической механике элементарная частица рассматривается как материальная точка, в каждый момент времени находящаяся

в определенной точке пространства, задаваемой вектором ºr (t) . В квантовой механике понятие «частица находится в точке про-

493

странства М» заменяется понятием: «с вероятностью P частица находится где-то внутри данного объема пространства V». Задачей квантовой механики является вычисление этой вероятности, которое можно сделать с помощью волновой функции частицы Ψ(x, y, z, t ) по формуле

P = ∫ Ψ Ψ*dV .

V

Здесь Ψ* — функция, комплексно сопряженная с Ψ, так как в общем случае волновая функция является функцией комплексного

переменного. Величина Ψ Ψ* = dP/dV называется плотностью вероятности распределения положений частицы в пространстве. Найти волновою функцию частицы можно, решив основное уравнение квантовой механики — уравнение Шредингера, имеющее вид:

где Ψ( ºr , t) — искомая волновая функция частицы U( ºr , t) — потенциальная энергия частицы.

В виду сложности данного уравнения далее мы рассмотрим ситуацию, когда потенциальная энергия частицы не зависит от времени

явно (U = U( ºr ) ), а частица может двигаться только по одной прямой (оси X). В этом случае уравнение Шредингера примет вид:

В этом уравнении «новая» волновая функция ψ связана со «ста-

называют стационарным (ψ не зависит от времени) уравнением Шредингера для одномерного движения частицы. Здесь Е — полная

x2

энергия частицы. Величина P = ∫ ψψ*dx есть вероятность того, что

x1

частица находится на отрезке [х1, х2] прямой X. Отметим, что функ-

ции — решения данного дифференциального уравнения — должны быть непрерывны вместе со своими первыми производными: ψ и dψ/dx — непрерывными функциями координаты х. Из этого обстоятельства в ряде задач возникает дискретность или непрерывность уровней энер-

494

гии частицы Е. Разберем несколько простейших одномерных задач квантовой механики:

1)частица находится в простейшей потенциальной яме;

2)частица движется в направлении прямоугольного потенциального барьера;

3)частица является гармоническим осциллятором, т.е. находится

вполе упругой силы, пропорциональной смещению частицы от положения равновесия.

Пример 30.10. Одномерная «потенциальная яма».

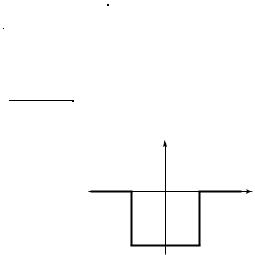
П о с т а н о в к а з а д а ч и . Зависимость потенциальной энергии частицы от координаты х имеет вид U(x) = 0, если | x | ≥ a и U(x) = – |U0|,

если | x | ≤ a. График этой функции, приведенный на рис. 30.12, и называется «потенциальной ямой». Необходимо определить характер движения частицы в зависимости от ее полной энергии.

К л а с с и ч е с к о е р е ш е н и е . Если полная энергия частицы Е заключена в интервале U0 < E < 0, то частица будет двигаться внутри

ямы, не покидая ее. Если полная энергия частицы Е > 0, то частица может находиться в любой области оси X. При этом энергетический спектр (область значений полной энергии Е ) непрерывен.

К в а н т о в о е р е ш е н и е .

1) U0 < E < 0. Внутри «ямы» уравнение Шредингера имеет вид

где k = 2m(E – U0 ) ⁄ $2 . Вне «ямы» имеем уравнение

где β = –2mE ⁄ $2 .

495

Записывая решение этих уравнений в общем виде, используя непрерывность волновой функции и ее производной, симметрию задачи, можно прийти к следующему результату: полная энергия частицы Е может принимать конечное число дискретных значений Е0,

Е1, …, Еn, лежащих в интервале (U0, 0), т.е. U0 < Е0 < Е1 < …< Еn< 0,

т.е. полная энергия частицы Е, находящейся в яме, квантована. Именно в этом заключено главное отличие результата квантовомеханической задачи от классического ее решения. При этом частица не может покинуть ямы.

2) E > 0. В этом случае оба подхода, классический и квантовый, дают один результат: частица может находиться в любой области оси X, ее полная энергия может принимать любое значение в интервале 0 < E< ×.

Пример 30.11. Одномерный «потенциальный барьер».

П о с т а н о в к а з а д а ч и . Зависимость потенциальной энергии частицы, показанная на рис. 30.13, вида U(x) = 0 при x < 0 и U(x) = U0 > 0

при x ≥ 0 называется потенциальным барьером. Частица с энергией Е движется слева направо по направлению к барьеру. Необходимо объяснить характер движения частицы в зависимости от ее полной энергии Е.

К л а с с и ч е с к о е р е ш е н и е . Если полная энергия частицы Е меньше «высоты» барьера U0, то частица отражается от него без

потери скорости; в противном случае (Е > U0) частица преодолевает барьер и движется в прежнем направлении с меньшей скоростью.

К в а н т о в о е р е ш е н и е . Необходимо решить два уравнения Шредингера:

В области x < 0 оно имеет вид

496

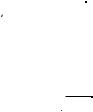
В области x > 0 оно записывается в виде

Полученная волновая функция должна быть непрерывна вместе с первой производной, что позволяет найти решение ψ(x). Отметим основные результаты решения уравнения Шредингера.

1) Е > U0. Существует ненулевая вероятность отражения частицы от барьера. Коэффициент отражения от барьера имеет вид:

k – β 2

R = ------------ ,

k + β

а коэффициент прохождения барьера

4kβ

D = --------------------- .

(k + β) 2

Отметим, что коэффициентом отражения R называют долю общего потока падающих частиц, приходящуюся на поток частиц отраженных. Аналогично определяется коэффициент прохождения барьера D.

2) E < U0. В этом случае коэффициент отражения R = 1, коэффи-

циент прохождения D = 0, но волновая функция справа от барьера имеет ненулевые значения, экспоненциально затухая с ростом х.

Особо интересен случай, когда барьер имеет конечную ширину d (рис. 30.14). Решение квантовомеханической задачи при E < U0

(классически непреодолимый барьер) позволяет определить ненулевой коэффициент прохождения D этого барьера в виде

Данное явление получило название «туннельного эффекта»; оно экспериментально открыто и используется в современных технологиях. Покажем на примитивном примере историю этого названия. На

рис. 30.15, а движущаяся со скоростью v < 2gh частица, которая должна подняться до точки А горки и вернуться назад, преодолевает горку и оказывается правее нее, двигаясь с прежней скоростью (рис. 30.15, б ). Все происходит так, как будто в горке имеется туннель

497

a) б)

A

v0

в)

Рис. 30. 15

(рис. 30.15, в), который «помог» частице преодолеть энергетический барьер.

Пример 30.12. Гармонический осциллятор. Назовем гармоническим осциллятором частицу, движущуюся по прямой линии, на которую действует возвращающая в положение равновесия сила, пропорциональная смещению частицы от положения равновесия. Масса частицы m, коэффициент пропорциональности между силой и смещением частицы k.

П о с т а н о в к а з а д а ч и. Описать характер движения частицы в зависимости от ее полной энергии E = p2 ⁄ (2m) + U(x) , где U(x) =

12

=--2-- kx (рис. 30.16).

E1

E0

Рис. 30. 16

498

К л а с с и ч е с к о е р е ш е н и е. Положительная полная энергия частицы E = p2 ⁄ (2m) + kx2 ⁄ 2 может быть любой. При фиксированной E = E0 частица совершает гармонические колебания с амплитудой

осциллятора можно найти, решив уравнение Шредингера:

Математическое решение этого уравнения оказывается достаточно сложным; можно указать, что его решения — волновые функции — выражаются как произведения экспонент на полиномы Чебышева — Эрмита. Анализ этих решений приводит к следующему выводу. Энергетические уровни осциллятора описываются формулой:

En = $ω(n + 1 ⁄ 2) ,

где n = 0, 1, 2, …

Разность энергий соседних уровней равна $ω (они находятся на равных расстояниях один от другого). Кроме того, существует ниж-

совершенно точно известны импульс px и координата х частицы, рав-

ные нулю. Соотношение неопределенностей (один из главных законов квантового мира) x px ≥ h утверждает, что это невозможно.

В заключение скажем, что точное математическое решение уравнения Шредингера даже в упомянутых выше «простейших» трех примерах очень сложно, поэтому мы не привели формул для волновых функций — его решений, а проанализировали следующие из этих решений выводы и различия результатов для классического и квантового решений этих задач.

499

ОГЛАВЛЕНИЕ

Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Раздел I. МЕХАНИКА . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1. Система координат. Система отсчета. Способы задания положения точки в пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.2. Понятие траектории. Кинематический закон движения материальной точки. Вектор перемещения. Путь . . . . . . . . . . . . . . . . . 6

1.3. Скорость. Нахождение пути. Ускорение . . . . . . . . . . . . . . . . . . . . . . . . 8 1.4. Кинематический закон движения материальной точки

с постоянным ускорением . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.5. Нормальное и тангенциальное ускорения . . . . . . . . . . . . . . . . . . . . . . . 10

1.6.Вращательное движение абсолютно твердого тела. Кинематические характеристики вращательного движения

вокруг неподвижной оси . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.7. Преобразования скорости и ускорения при переходе

к другой системе отсчета. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

Глава 2. Динамика поступательного движения твердого тела.. . . . . . . . 20

Глава 3. Работа и энергия в механике поступательного движения . . . . 33

Глава 4. Динамика вращательного движения твердого тела . . . . . . . . . 46

4.1. Момент импульса точки относительно полюса. . . . . . . . . . . . . . . . . . . 46

500