то дифракция от N щелей не является простой суммой дифракционных картин от каждой щели в отдельности. Для расчета такой картины необходимо учитывать взаимную интерференцию колебаний, приходящих от разных щелей.
Главные максимумы дифракционной картины отвечают таким углам дифракции, при которых соответственные лучи, идущие от разных щелей, приводят к перераспределению интенсивности в сторону ее увеличения (колебания взаимно «усиливают» одно другое). Поэтому результирующая амплитуда колебания в данной точке на экране
º |
n |
º |
|
A рез |
= ∑ |
A i |
, |
|
i = 1 |
|
|
где амплитуда Аi соответствует колебанию, приходящему от одной
щели. Так как все щели занимают по отношению к углу дифракции совершенно одинаковое положение, то
A1 = A2 = … = AN = A и Aрез = NA.
Поэтому:
Iрез = N 2I,
где I — интенсивность, создаваемая одной щелью. Таким образом, интенсивность главного максимума картины, наблюдаемой от диф-
ракционной решетки, в N 2 раз больше интенсивности максимума картины от одной щели.
Разность фаз колебаний δ связана с разностью хода соотношением
δ = 2π --λ-- ,
где λ — длина световой волны.
Из рис. 27.34 видно, что = d sin ϕ. Подставим это выражение в последнюю формулу и учтем, что в максимумах интенсивности колебания должны происходить синфазно, т.е. d = ± 2mπ, где m = = 0, 1, 2, 3 … Как результат имеем:
2π |
d sin |
ϕ , |
± 2mπ = ------ |
λ |
|
|
или |
|
|
d sin ϕ = ± mλ, |
(27.18) |
где m = 0, 1, 2, 3, … |
|
|
Условие (27.18) определяет положения главных максимумов интенсивности.

Главные минимумы соответствуют таким направлениям дифрагирующих лучей, при которых получается условие минимума для одной щели (см. (27.14)):
где b — ширина щели, k = 1, 2, 3, …
Дело в том, что главные минимумы соответствуют результату интерференции лучей в пределах каждой отдельной щели. И если каждая щель в данном направлении света не посылает, то и от N щелей в этом направлении света не будет.
Добавочные минимумы соответствуют таким углам, при которых в данном направлении каждая щель свет посылает. Но вследствие интерференции колебаний, приходящих от разных щелей, результирующая амплитуда оказывается равной нулю. Эти колебания взаимно
гасятся: |
|
|
|
|
|
º |
n º |
|
|
|
A |
рез |
= ∑ A i |
= 0 |
и |
Iрез = 0. |
i = 1
Воспользуемся графическим методом сложения амплитуд. Сло-
|
º |
|
º |
|
жим этим методом амплитуды |
A |
1 |
и |
A |
2 двух колебаний по правилу |
параллелограмма (рис. 27.35). |
|
|
|
|
|
|
º |
|
|
º |
|
º |
(ϕ1 и ϕ2 начальные фазы |
Из рисунка видно, что A рез |
= |
|
A 1 |
+ |
A 2 |
соответственно первого и второго колебательного процессов). Но
º
совершенно аналогично A рез можно получить из сложения тех же амплитуд по правилу треугольника (рис. 27.36). На рисунке δ = ϕ2 – ϕ1 является разностью фаз колебаний.
Если колебаний не два, а N (от N щелей), причем с одинаковыми амплитудами A1 = A2 = … = AN = A, то картина сложения амплитуд
будет соответствовать представленной на рис. 27.37, |
из которого |
º |
|
видно, что для получения минимума дифракции ( A рез |
= 0) нужно, |
чтобы амплитуды складывались в виде замкнутого многоугольника.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
Aрез |
|
|
|
|
Aрез |
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ2–ϕ1 |
|
|
|
ϕ2 |
|
ϕ1 |
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
ϕ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опорная ось |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Опорная ось |
|
|
|
|
|
Рис. 27. 35 |
Рис. 27. 36 |
|
|
δ = ϕ3 – ϕ2
A2
δ = ϕ2 – ϕ1
Опорная ось
Рис. 27. 37
Между любыми соседними векторами амплитуд должен быть одинаковый угол δ. Этот угол, с одной стороны, равен разности фаз этих
колебаний δ = 2π / N, но с другой стороны, δ = 2πΔ / λ . И, следовательно, 2π / N = 2πΔ / λ . Но = d sin ϕ, поэтому d sin ϕ = λ / N.
В дифракционной картине наблюдается не один минимум, и для нахождения остальных нужно обойти многоугольник 2 раза, 3 раза и т.д.:
|
= d sin ϕ = |
λ |
2λ |
; |
3λ |
; |
… , |
|
---- ; |
------ |
------ |
|
|
N |
N |
|
N |
|
|
т.е. |
|
|
|
|
|
|
|
d sin ϕ = k ′ -λ--- |
где k ′ = 1, 2, 3, … (N – 1), (N + 1), … |
N |
|
|
|
|
|
|
|
При m = 0, N, 2N, … наблюдаются главные максимумы, поэтому эти значения исключаются. Таким образом, между двумя главными максимумами, соответствующими условию d sin ϕ = mλ , где m = 0, N, 2N, …, лежат по N – 1 добавочных минимумов, определяемых разностью хода
d sin ϕ = mλ + k ′′ λ / N, |
(27.20) |
где k ′′ пробегает значения от 1 до N – 1 (k ′′ ≠ N ). Между добавочными минимумами располагаются вторичные максимумы. Число таких максимумов, приходящихся на промежуток между главными соседними максимумами, равно N – 2. Интенсивность вторичных максимумов очень мала. Самое большее′ она составляет 1 / 22 интенсивности ближайшего главного максимума.
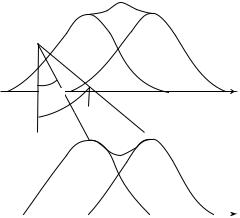
На рис. 27.38 приведен график функции I = f(sin ϕ) для N = 4 и d / b = 3. Штриховая кривая, проходящая через вершины главных макси-
мумов, изображает интенсивность от одной щели, умноженную на N 2.
403

I
Условие главных максимувов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
λ |
|
|
|
2λ |
|
|
|
3λ |
4λ |
5λ |
6 |
λ |
|
Nd |
|
|
|
d |
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
d |
d |
d |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
2λ |
|
|
|
|
|
—1– |
1 |
˜ |
λ |
|
—2– |
1 |
˜ |
λ |
|
|
|
|
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
d |
|
N |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
—1+ |
|
|
˜ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
λ |
|
—2+ |
1 |
˜ |
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
d |
|
N |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие добавочных минимумов |
|
|
|
|
|
|
|
|
|
|
|
Условие главных минимумов |
Рис. 27. 38
При данном отношении, d / b = 3, как видно из рисунка, главные максимумы третьего, шестого и т.д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают. Из формул (27.18) и (27.19) вытекает, что главный максимум m-го порядка приходится на k-й минимум от одной щели, если будет выполнено условие m / d = k / b или m / k = d / b.
Это возможно, если d / b равно отношению двух целых чисел.
Тогда главные максимумы с номерами равными |
d |
d |
d |
и т.д. |
---- , 2 |
---- , 3 |
---- |
|
b |
b |
b |
|
пропадают.
Положение главных максимумов зависит от длины волны λ. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр. Фиолетовый цвет спектра ближе
кцентру дифракционной картины, красный — к периферии.
Сучетом того, что модуль sin ϕ не может превысить единицу, из анализа формулы дифракционной решетки для главных максимумов вытекает, что
sin ϕ = mλ ⁄ d ≤ 1 .
Отсюда следует, что дифракционная картина будет отсутствовать, если d < λ. Если d >> λ, картина перестает быть отчетливой, так как угловое расстояние между соседними максимумами станет столь малым, что они начнут перекрываться. Наилучшие результаты получаются тогда, когда d незначительно превышает λ.
Чтобы максимумы близких длин волн различались как разные (разрешались) нужно, чтобы выполнялся критерий Рэлея (Д.У. Рэлей
(1842—1919)). Согласно этому критерию максимумы (спектральные линии) считаются полностью разрешенными, если середина одного максимума совпадает с краем другого, т.е. два близких максимума воспринимаются глазом раздельно, если интенсивность в промежутке между ними составляет не более 80 % интенсивности максимума.
На рис. 27.39 представлены два варианта взаимного расположения двух соседних максимумов. В варианте рис. 27.39, а они сливаются для глаза, в варианте рис. 27.39, б считаются полностью разрешенными. Для варианта рис. 27.39, б запишем условия, дающие положения максимумов m-го порядка для волн с λ1 и λ2:
d sin ϕ ′ |
= mλ |
1 |
, |
здесь λ = λ |
1 |
; |
max |
|
|
|
|
|
|
|
d sin ϕ ″ |
= mλ |
2 |
, |
где λ |
2 |
= λ |
1 |
+ δλ . |
max |
|
|
|
|
|
Для перехода от m-го максимума для длины волны λ1 к соответ-
ствующему минимуму (краю максимума) необходимо изменить направление дифрагирующего луча так, чтобы разность изменилась на λ1 / N, где N — число штрихов решетки. Таким образом, минимум
для света с длиной волны λ1 наблюдается в направлении ϕmin.
Согласно критерию Рэлея |
|
|
|
|
ϕ ″ |
|
= ϕ |
min |
, |
max |
|
|
откуда |
|
|
|
|
mλ2 = mλ1 + λ1 / N, |
или |
λ1 / ( λ2 – λ1 ) = mN. |
λλ+δλ
Рис. 27. 39
Так как λ2 и λ1 отличаются на δλ, то |
|
R = λ / (δλ) = mN, |
(27.21) |
где R называется разрешающей силой дифракционной решетки и является одной из основных характеристик дифракционной решетки.
Разрешающая сила равна произведению порядка дифракционного максимума на полное число штрихов решетки. Для данной дифракционной решетки разрешающая сила тем больше, чем больше порядок дифракционного максимума. Для данного максимума разрешающая сила тем больше, чем больше число штрихов N. Итак, как следует из формулы (27.21), разрешающая сила определяет минимальную разность длин волн δλ, при которой две линии воспринимаются в спектре раздельно.
Другой важнейшей характеристикой дифракционной решетки является угловая дисперсия:
δϕ
D = -δλ----- ,
где δϕ — угловое расстояние между спектральными линиями, различающимися по длине волны на δλ.
Взяв производную от левой и правой частей уравнения, выражающего условие главных максимумов для дифракционной решетки (27.18), получим:
d cos ϕ δϕ = mδλ .
Отсюда
D = |
δϕ |
= |
m |
------ |
--------------- . |
|
δλ |
|
d cos ϕ |
Для небольших углов дифракции cos ϕ ≈ 1, поэтому D ≈ m / d .
Таким образом, чем больше порядок максимума m, тем больше дисперсия, т.е. угловое расстояние между двумя спектральными линиями в этом порядке m больше по сравнению с угловым расстоянием между теми же по цвету линиями в максимуме меньшего порядка (максимумы становятся шире с увеличением номера порядка m). Дисперсия зависит и от периода решетки d: c увеличением периода она уменьшается.
Линейной дисперсией называется величина
δl
Dлин = -δλ----- ,
где δl — линейное расстояние на экране между двумя спектральными линиями, отличающимися по длине волны на δλ .
Линейная дисперсия связана с фокусным расстоянием f линзы, собирающей дифрагирующие лучи на экране, и угловой дисперсией D (при небольших углах ϕ) соотношением
D |
|
= f D, или |
D |
|
m |
лин |
лин |
= f --- . |
|
|
|
d |
|
|
|
|
|
Современные технологии позволяют изготавливать дифракционные решетки с очень большим числом штрихов на 1 мм длины решетки. Например, 500 штрих / мм, 600 штрих / мм, 1200 штрих / мм. Решетка с N1 = 1200 штрих / мм обладает прекрасной разрешающей
силой. Максимум первого порядка дифракционной картины, полученный от этой решетки, имеет ширину около 700 мм. Второй порядок от такой решетки не наблюдается. Действительно, d sin ϕ = mλ , где d = 1 / N1. Положим m = 2 и λ = 500 нм. Тогда
sin ϕ = mλN |
|
= 2æ50æ10 |
– 9 |
1 |
1 |
|
æ1200 ------------ = 1,2 . |
|
|
|
10– 3 |
|
|
|
|
Но sin ϕ ≤ 1, следовательно, второго порядка нет и вся дифракционная картина представляет собой два максимума первого порядка, симметрично расположенных относительно максимума нулевого порядка.
Выше была рассмотрена так называемая одномерная дифракционная решетка, работающая на пропускание света. Существуют более сложные решетки — двумерные и трехмерные (пространственные). Для образования двумерной решетки нужно сложить две одномерные так, чтобы их щели были взаимно перпендикулярны. Для каждой из этих решеток условия наблюдения главных максимумов предстанут в виде двух уравнений:
d1 sin ϕ1 = ± m1λ ; |
(m1 = 0, 1, 2, …); |
(27.22) |
d2 sin ϕ2 = ± m2λ ; |
(m2 = 0, 1, 2, …). |
(27.23) |
Измеряя углы дифракции ϕ1 и ϕ2 и зная длину волны λ, находим по формулам (27.22), (27.23) периоды двумерной решетки d1 и d2.
Подобная двумерная структура дает дифракционную картину в виде симметрично расположенных пятен, каждому из которых соответствуют два целочисленных значения m1 и m2.
Набор равноотстоящих и параллельных друг другу двумерных решеток представляет собой трехмерную пространственную решетку. Такими естественными пространственными решетками являются все кристаллические тела. Период кристаллической решетки d (расстояние между соседними атомами) составляет около
10–10 м (0,1 нм). Для наблюдения дифракции на решетке должно выполняться условие d > λ. Поэтому видимый свет с диапазоном

длин волн 400—750 нм на кристаллической решетке не дифрагирует. Условие d > λ выполняется только для рентгеновских лучей. Впервые дифракция рентгеновских лучей от кристаллов наблюдалась в 1913 г. в опыте М. Лауэ (1879—1960), В. Фридриха (1883—1968) и П. Книппинга (1883—1935). На рис. 27.40 приведена дифракционная картина берилла.
Метод Ю.В. Вульфа (1863—1925), У.Г. Брэгга (1862—1942) и У.Л. Брэгга (1890—1971) позволяет рассчитать дифракционную картину от кристаллической решетки.
Рассечем кристалл рядом параллельных кристаллических плоскос-
тей, расстояние между которыми d ≈ 10– 10 м (рис. 27.41). Направим на кристалл плоскую электромагнитную волну под углом скольжения θ. Отразившиеся от кристаллических плоскостей вторичные волны будут интерферировать, так как являются когерентными волнами. Разность хода между двумя лучами 1 и 2, отразившимися от соседних кристаллических плоскостей, может быть найдена из АВС: ВС = d sin θ и, следовательно, разность хода ВСD = 2d sin θ. Поэтому направления, для которых получаются дифракционные максимумы, определяются условием
2d sin θ = ± mλ ,
где m = 1, 2, 3, … Это соотношение называется формулой Брэгга— Вульфа.
Дифракция рентгеновских лучей позволяет решить две фундаментальные задачи:
1. Изучение структуры кристалла — рентгеноструктурный анализ, т.е., изучая дифракцию рентгеновских лучей известной длины волны на кристаллических решетках неизвестной структуры, можно определить период решетки и изучить расположение атомов в кристалле.
2
1
θ A
A  θ
θ

2. Исследование спектрального состава рентгеновского излучения — рентгеноспектроскопия, т.е., изучая дифракцию рентгеновского излучения неизвестной длины волны на кристаллах известной структуры, можно определять длины волн рентгеновского излучения.
Пример 27.6. На дифракционную решетку нормально к ее поверхности падает плоская монохроматическая световая волна (λ = 500 нм). Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на L = 1 м. Расстояние между двумя максимумами первого порядка на экране l = 20,2 см. Найдите: 1) период дифракционной решетки d ; 2) число штрихов N1,
приходящихся на 1 мм длины решетки; 3) число порядков, которое дает решетка; 4) угол отклонения лучей ϕ, соответствующих последнему дифракционному максимуму.
1. Запишем формулу для главных максимумов дифракционной решетки (27.18) для нашей конкретной задачи, опуская знак «– » и учитывая, что m = 1, а ϕ = ϕ1 (под углом ϕ1 виден максимум первого
порядка):
Из ВАD (рис. 27.42) найдем tg ϕ1 = l / (2L ) = 0,1; ϕ1 = 5,8°. Для таких малых углов sin ϕ1 ≈ tg ϕ1. Подставляя вместо sin ϕ1 в уравнение (27.24) tg ϕ1, получаем
d= 2λL / l = 4,95 мкм.
2.По определению число штрихов, приходящихся на единицу длины решетки, равно величине, обратной периоду решетки:
N1 = 1 / d = 202 штрих / мм.
d
Решётка a b
A
I
Линза
ϕ1
L
Рис. 27. 42

3. Число порядков найдем из условия, что угол отклонения лучей решеткой не должен превышать 90°, т.е. (sin ϕ) = 1, и, следовательно, уравнение главных максимумов (27.18) d sin ϕ = mλ запишется в виде d = mλ, или
m = d / λ = 9,9.
Но число m должно быть целочисленным и не должно быть равно 10. Поэтому m = 9. Полное число порядков (по обе стороны от максимума нулевого порядка, включая его) равно 2m + 1, т.е. 19.
4. Максимальный угол, под которым виден самый дальний от центра картины максимум с номером порядка m = 9, рассчитывается по формуле
d sin ϕmax = mλ,
отсюда
sin ϕmax = mλ / d ; ϕmax = arcsin (mλ / d ) = 65,4°.
Пример 27.7. Дифракционная решетка, имеющая N1 = 500 штри-
хов на 1 мм длины решетки, дает на экране, отстоящем от линзы на расстояниe L = 1 м, спектр. Определите, на каком расстоянии l1 одна
от другрй будут находиться фиолетовые границы спектров второго порядка (λф = 400 нм).
Условие главных максимумов дифракционной картины (27.18):
d sin ϕ = ± mλ ,
без знака «–», с учетом, что d = 1 / N1, а m = 2, запишется в виде
1 |
λ ; sin ϕ = 2λ N |
|
= 0,4; |
ϕ = 23,6°. |
------ sin ϕ = 2 |
1 |
N1 |
|
|
|
|
|
|
|
|
|
|
|
Решётка |
|
A |
|
|
|
|
I |
|
|
|
|
ϕ |
|
|
Линза |
|
|
|
|
L |
|
|
|
|
Рис. 27. 43









 A
A 