
Специально для групп С-12 / Общая физика_под ред. Белокопытова_2016 -506с
.pdf
O
Экран
Линза
i2
i1

 .. n
.. n
Рис. 27. 14
ференционную картину можно наблюдать, поставив на пути отраженных лучей тонкую линзу. Такие линзы — таутохронны (они не вносят дополнительной разности хода для параллельных лучей, падающих на линзу). Кроме того, линза собирает параллельные лучи в своей фокальной плоскости. Если в этой плоскости поместить экран, то именно на нем можно наблюдать чередование темных и светлых полос. Такая интерференционная картина получила название полос равного наклона.
27.5. Дифракция света
Дифракцией называется совокупность явлений, связанных с распространением света в среде с резкими неоднородностями (препятствиями). Если свет в такой среде встречает препятствие, то он отклоняется от прямолинейного распространения и проникает в область геометрической тени. При выполнении определенных условий можно наблюдать явление дифракции в виде дифракционной (интерференционной) картины. Эта картина представляет собой для монохроматического света систему чередующихся в зависимости от формы препятствия светлых и темных колец или систему светлых и темных параллельных полос. Под препятствиями понимаются прозрачные (в виде отверстий) и непрозрачные (в виде преград) образования малых линейных размеров.
Между дифракцией и интерференцией нет существенного физического различия. Оба явления заключаются в перераспределении
381


Разобьем волновую поверхность на элементарные источники S1, S2, …, Sn . Эти источники будут когерентными, так как они порож-
даются одной и той же волной и представляют собой элементы разбиения данной волновой поверхности. Результирующее колебание в точке Р есть результат интерференции всех вторичных волн, приходящих от этих источников в точку Р с учетом их амплитуды и фазы. При этом стоит учитывать те элементы волновой поверхности, которые не загораживаются каким-либо препятствием.
Способы разбиения волновой поверхности на элементарные источники зависят от характера задачи. О. Френель предложил оригинальный метод разбиения волновой поверхности на зоны (зоны Френеля).
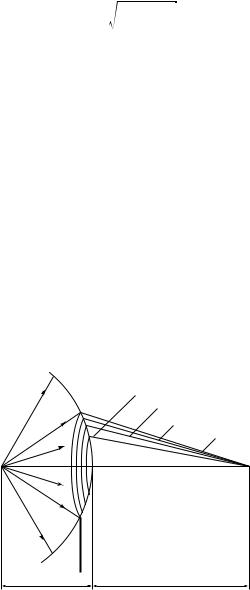
Рассмотрим следующий пример. Поместим точечный монохроматический источник света S в фокус слева от собирающей линзы Л (рис. 27.17). Справа от линзы образуется плоская монохроматическая световая волна. Выделим на ней произвольную плоскую волновую поверхность F и разобьем волновую поверхность на элементарные источники — зоны Френеля. Для этого с центром в точке наблюдения Р, лежащей на оси симметрии, проведем ряд концентрических сфер. Первая сфера с наименьшим радиусом L, равным расстоянию от точки Р до волновой поверхности, должна коснуться этой поверхности. Все остальные пересекают волновую поверхность, при этом радиус каждой последующей сферы должен отличаться от радиуса предыдущей на половину длины волны λ /2. Со стороны точки наблюдения Р границы зон на волновой поверхности представляют собой линии пересечения сфер и волновой поверхности в виде концентрических окружностей (рис. 27.18). Поэтому все зоны, за исключением первой — круга, являются кольцами. На рис. 27.18 ρ1, ρ2, ρ3
являются радиусами соответствующих зон Френеля, а R — радиусом
Л |
F |
|
λ |
|
|
|
L+2 |
|
|
|
|
|
2 |
|
|
|
λ |
|
ρ2 |
|
L+ |
|
ρ1 |
|
S |
2 |
P |
ρ3 |
R
L
Рис. 27. 18
Рис. 27. 17
383






 .
. 

 .
. .
. .
. .
.
 Lλ ; ρ
Lλ ; ρ
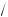 2Lλ ; ρ
2Lλ ; ρ
 mLλ ; ρ
mLλ ; ρ
 (m – 1)Lλ .
(m – 1)Lλ .
 Lλ ≈ 0,77 мм.
Lλ ≈ 0,77 мм.