
Специально для групп С-12 / Общая физика_под ред. Белокопытова_2016 -506с
.pdf
dS2
2
E 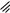 E
E
S2
0 |
1 |
+ |
dS1 |
Q |
S1 |
Рис. 15. 18
и S2 . Полный поток напряженности через всю поверхность S равен алгебраической сумме потоков через эти части:
Φ = |
º º |
= ∫ |
º º |
+ ∫ |
º º |
= Φ1 + Φ2. |
E d S |
E d S |
E d S |
||||
|
S |
S1 |
|
S2 |
|
|
º
Для всех элементов поверхности S1 углы между векторами E и
º
внешними нормалями n (при Q > 0) — тупые; для всех элементов поверхности S2 — острые. Следовательно,
º º
Φ1 = ∫ E d S =
S1
∫ |
º º |
) < 0; |
EdS cos ( E , n |
||
S1 |
|
|
(15.24)
º º
Φ2 = ∫ E d S =
S2
∫ |
º º |
) > 0. |
EdS cos ( E , n |
||
S2 |
|
|
Поскольку поверхности S1 и S2 видны из точки расположения заряда Q под одним и тем же телесным углом Ω0 , то согласно (15.22)
|Φ1| = |Φ2| = |
|
Q |
|
Ω0 |
|
|
------------ |
. Отсюда с учетом (15.24) получаем |
|
||||
4 |
πε |
0 |
|
|||
|
|
|
|
|||
|
|
|
|
|
Φ = Φ1 + Φ2 = 0. |
(15.25) |
Обобщим полученные результаты. Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность пропорционален алгебраической сумме зарядов, охваченных этой поверхностью:
n
|
|
∑ Qi охв |
|
º º |
i = 1 |
(15.26) |
|
E |
d S |
= ---------------------- . |
|
S |
|
ε0 |
|
|
|
|
|
201

Полученное утверждение называется теоремой Гаусса для электростатического поля в вакууме. Замкнутую поверхность S, фигурирующую в формулировке теоремы, часто называют гауссовой поверхностью. Отметим, что коэффициент пропорциональности между потоком напряженности и суммой зарядов, охваченных этой поверхностью, определен выбором системы единиц физических величин. В СИ этот коэффициент равен 1 / ε0. В других системах еди-
ниц он принимает другие значения.
15.7. Примеры использования теоремы Гаусса
Теорему Гаусса (15.26) удобно использовать для расчета напряженности электростатических полей, созданных симметричными системами зарядов. В этих случаях можно так выбрать гауссову поверхность, что поток вектора напряженности поля через нее легко выражается с помощью искомого значения модуля напряженности. Решение задачи о нахождении напряженности электростатического поля в какой-либо точке пространства осуществляется в несколько этапов.
1.Исходя из симметрии распределения заданной системы зарядов
впространстве, построить силовые линии поля, т.е. определить
º
направление вектора E в любой точке пространства.
2. Выбрать «удобную» замкнутую гауссову поверхность, отвечающую следующим требованиям:
а) она должна проходить через исследуемую точку; б) площадь поверхности должна быть известна;
в) модуль напряженности поля должен быть постоянен в точках всей поверхности или хотя бы ее части;
º
г) угол между E и внешней нормалью к поверхности должен быть известен в любой точке поверхности (это обеспечивается выполнением п. 1).
3. Получить выражение для потока напряженности поля через выбранную поверхность. Если выполнено условие п. 2в, то
º º |
= E1 ∫ |
º |
º |
) dS + E2 |
∫ |
|
º |
º |
|
|
E d S |
cos ( E |
, d S |
cos ( E |
, d S |
) dS + … + |
|||||
S |
S1 |
|
|
|
|
S2 |
|
|
|
|
|
|
|
|
º |
|
|
º |
|
|
|
|
|
+ … + EN ∫ cos ( E |
, |
d S |
) dS , |
|
||||
SN
где Ei — постоянный модуль напряженности поля во всех точках части поверхности S i .
202
4.Определить алгебраическую сумму зарядов, охваченных поверхностью S.
5.Применить теорему, т.е. приравнять результаты, полученные в
пп.3 и 4, с учетом коэффициента пропорциональности.
Пример 15.6. Определим напряженность электростатического поля во всех точках пространства, если электрический заряд Q > 0 равномерно распределен в пространстве в виде шара радиусом R.
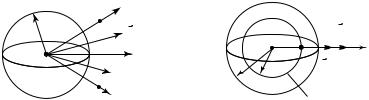
1. Исходя из условий симметричного распределения заряда, изобразим силовые линии его электрического поля. Поскольку данное распределение заряда обладает сферической симметрией, силовые линии поля будут исходить из центра шара по радиальным направлениям (на рис. 15.19 показаны только четыре силовые линии).
Кроме того, исходя из симметрии системы, можно утверждать, что модуль напряженности поля во всех точках, равноудаленных от центра шара, должен быть одинаковым. Это справедливо, например, для точек А и В (рис. 15.19), находящихся на одинаковом расстоянии от центра симметрии системы.
º
Cледовательно, направление и модуль вектора E будут зависеть только от радиальной координаты исследуемой точки пространства. Для задания такой координаты r выберем произвольную радиальную ось Or, выходящую из центра шара.
2. Определим напряженность поля в произвольной точке C, находящейся внутри шара на расстоянии r от его центра. Для этого в качестве гауссовой поверхности выберем сферическую поверхность радиусом r, центр которой совпадает с центром заряженного шара. На рис. 15.20 штриховой окружностью радиусом r показана линия пересечения этой поверхности с плоскостью чертежа.
Cледствием симметрии системы является равенство модуля вектора напряженности поля во всех точках поверхности, и равенство
º
угла между E и внешней нормалью к поверхности во всех точках поверхности нулю.
|
A |
|
Q |
|
Q |
|
|
|
|
|
|
|
n |
|
R |
E |
|
|
|
|
|
|
|
|
|
r |
|
O |
|
|
O |
|
C |
r |
|
|
|
|
E |
|
|
R |
r |
|
|
|
|
|
|
|
B |
|
S |
|
|
Рис. 15. 19 |
|
Рис. 15. 20 |
|
203

º
3. Определим поток вектора E через гауссову поверхность:
º º |
= E |
º |
, |
º |
) dS = E dS = E 4πr 2. (15.27) |
|
E |
d S |
cos ( E |
d S |
|||
S |
|
S |
|
|
|
S |
4. Определим алгебраическую сумму зарядов, охваченных поверхностью S. В данном случае электрический заряд, охваченный гауссовой поверхностью, — это часть всего заряда. Определим эту часть заряда через объемную плотность заряда и объем, ограниченный гауссовой поверхностью:
Q |
|
= ρV |
|
= |
Q |
|
4 |
πr 3 = |
Q r 3 |
(15.28) |
|
охв |
охв |
---------------- |
- |
---- |
---------- |
. |
|||||
|
|
|
4 |
3 |
3 |
|
R |
3 |
|
||
|
|
|
|
|
---- πR |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
5. Применим теорему Гаусса, приравняв (15.27) и (15.28) с учетом коэффициента 1 / ε0 :
E4πr |
2 |
= |
1 |
Q r 3 |
|
---- |
---------- . |
|
|||
|
|
|
ε0 |
R3 |
|
Отсюда получим, что при r < R |
|
|
|
|
|
|
|
1 |
|
Q r |
|
E = |
------------ |
------- |
|
||
4πε0 |
R3 . |
(15.29) |
|||
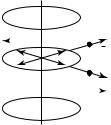
Применим эту процедуру для определения напряженности поля вне шарового скопления заряда. Выберем гауссову поверхность в виде сферы радиусом r > R, проходящей через произвольную точку D, находящуюся вне зарядов. На рис. 15.21 штриховой окружностью радиусом r показана линия пересечения этой поверхности с плоскостью чертежа.
º
Выражение для потока вектора E через гауссову поверхность сохранит прежний вид (15.27). Заряд, охваченный поверхностью, представляет собой полный заряд шара: Qохв = Q. Согласно теореме
|
Q |
|
|
|
|
|
|
|
D |
|
Er |
1 |
|
|
O |
E |
|
|
|
|
|
|
|
|
~ r 2 |
|
|
|
|
n |
r |
~r |
|
|
|
|
|
|
|
||
R |
|
|
|
|
|
|
r |
S |
|
|
0 |
R |
r |
|
Рис. 15.21 |
|
|
|
Рис. 15. 22 |
|
204
Гаусса |
получим, что при r |
> |
R имеет |
место соотношение |
|||
E4πr 2 |
= |
1 |
Q . Откуда |
|
|
|
|
---- |
|
|
|
||||
|
|
ε |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = |
1 |
Q |
(15.30) |
|
|
|
|
------------ ----- . |
|||
|
|
|
|
|
4πε |
0 r 2 |
|
Окончательный вид зависимости модуля напряженности от координаты r можно представить так:
|
1 |
Q r |
|
r ≤ R; |
|
|
------------ |
------- |
при |
||
4πε0 |
R3 |
||||
|
|
|
|||
E(r) = |
|
Q |
|
|
|
|
1 |
|
r ≥ R. |
||
------------ ----- |
при |
||||
|
4πε0 |
r 2 |
|||
|
|
||||
|
|
|
|
|
|
При построении графической зависимости E(r) (рис. 15.22) обратим внимание на то, что выражения (15.29) и (15.30) дают одинаковые значения модуля напряженности поля при r = R:
E(R) = |
|
1 |
|
Q |
------------ |
------ |
|||
4 |
πε |
0 R 2 . |
||
Пример 15.7. Определим напряженность электростатического поля во всех точках пространства, если электрический заряд равномерно распределен с поверхностной плотностью σ > 0 по поверхности весьма длинного цилиндра с радиусом основания R.
1. Определим из условий симметрии и изобразим графически линии напряженности электрического поля. Поскольку данное распределение заряда обладает осевой симметрией, силовые линии поля (если поле существует) будут исходить из точек оси цилиндра по радиальным направлениям (на рис. 15.23 показаны четыре силовые линии электрического поля).
Вследствие осевой симметрии системы, модуль напряженности
поля во всех точках, равноудаленных от оси |
|
|
|
|
|
|
|
|
системы, должен быть одинаковым: такие точки, |
|
|
|
|
|
|||
как, например, точки А и В, находятся на одина- |
|
|
|
|
||||
|
|
|
|
|
|
|
||
ковом расстоянии от оси симметрии системы. |
|
|
R |
|
|
A |
||
Следовательно, направление и модуль век- |
|
|
|
|
|
E |
||
º |
будут зависеть только от радиальной |
|
|
|
|
|
B |
|
тора E |
|
|
|
|
|
|
|
|
координаты исследуемой точки пространства. |
|
|
|
O |
|
|
|
|
|
|
|
|
|
r |
|||
Для задания такой координаты r выберем про- |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
извольную радиальную ось O r, направленную |
|
|
|
|
|
|
|
|
перпендикулярно оси цилиндра. |
|
|
|
Рис. 15. 23 |
||||
|
|
|
|
|
||||
205
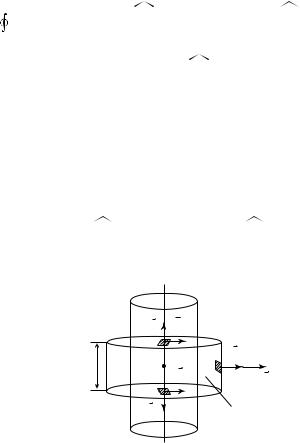
2. Определим напряженность поля в произвольной точке C, находящейся вне цилиндра и имеющей координату r > R. Для этого выберем замкнутую поверхность S в виде поверхности цилиндра высотой Н и радиусом r, ось которого совпадает с осью заряженного цилиндра (рис. 15.24).
Модуль напряженности поля постоянен во всех точках боковой поверхности цилиндра, вследствие симметрии системы. Угол между
º
E и внешней нормалью к поверхности во всех точках боковой поверхности цилиндра равен нулю, а во всех точках верхнего и нижнего оснований гауссова цилиндра равен π / 2.
3. Определим поток вектора напряженности через замкнутую поверхность S.
º º |
= E1 ∫ |
º |
|
º |
|
º |
º |
E d S |
cos ( E |
, d S 1) dS + E2 ∫ |
cos ( E |
, d S 2 ) dS + |
|||
S |
S1 |
|
|
|
S2 |
|
|
|
|
+ E3 ∫ |
º |
º |
|
|
|
|
|
cos ( E |
, d S3 ) dS , |
|
|||
|
|
|
S3 |
|
|
|
|
где S1 — площадь верхнего основания цилиндра; S2 — площадь нижнего основания цилиндра; S3 — площадь боковой поверхности
º º º
цилиндра; d S 1 , d S 2 , d S3 — векторы соответствующих элементар-
ных площадок. Учитывая соображения, изложенные при осуществлении этапа 2, получаем:
E1 ∫ |
º |
|
º |
∫ |
º |
|
º |
cos ( E |
, |
d S 1) dS = E2 |
cos ( E |
, |
d S 2 ) dS = 0; |
||
S1 |
|
|
|
S2 |
|
|
|
H
dS1 E1 |
|
|
|
dS3 |
|
O |
|
|
E2 |
C |
E3 |
dS2 |
S |
|
Рис. 15. 24
206

E3 ∫ cos ( |
º |
|
º |
|
E |
, |
d S3 ) dS = E3S3. |
|
|
S3 |
|
|
|
|
Таким образом, |
|
|
|
|
º º |
|
|
|
|
E d S |
= E3S3 = E 2πrH . |
(15.31) |
||
S
4. Определим алгебраическую сумму зарядов, охваченных поверхностью гауссова цилиндра. В данном случае электрический заряд, попавший внутрь гауссовой поверхности, — это часть полного заряда цилиндра. Эту часть можно найти, умножив площадь боковой поверхности заряженного цилиндра, охваченного гауссовой поверхностью, на поверхностную плотность заряда:
|
|
|
Qохв = σ 2πRH . |
|
|
|
(15.32) |
5. Приравняв |
|
(15.31) и (15.32) с учетом |
коэффициента 1 / ε0 , |
||||
имеем: E 2πrH = |
1 |
σ 2πRH . Отсюда следует, что E = |
σR |
||||
---- |
------- |
||||||
ε |
0 |
ε |
0 |
r . |
|||
|
|
|
|
|
|
||
Повторим все действия для определения напряженности поля внутри заряженного цилиндра. В этом случае выберем гауссову поверхность в виде цилиндрической поверхности, боковая поверхность, которой проходит через произвольную точку D, находящуюся на расстоянии r < R (рис. 15.25).
º
Выражение для потока E через гауссову поверхность сохранит прежний вид (15.31). Но в этом случае внутри гауссовой поверх-
ности нет зарядов, поэтому E 2πrH = |
1 |
0 откуда следует E = 0. |
|
ε |
|
||
|
---- |
|
|
|
|
0 |
|
H
|
Er |
|
D |
E |
|
O |
r |
|
|
|
|
|
R |
r |
R |
Рис. 15. 26 |
|
Рис. 15. 25
207
Окончательно зависимость модуля напряженности от радиальной координаты можно представить следующим образом:
0 |
|
при |
r < R; |
||
|
|
|
|
|
|
E(r) = |
σR |
при |
r ≥ R. |
||
|
------- |
||||
ε |
|
r |
|
|
|
|
|
0 |
|
|
|
График полученной зависимости изображен на рис. 15.26. Видно, что при значении r = R график имеет разрыв. Отсюда, в частности, можно сделать вывод, что при переходе через поверхность, заряженную с поверхностной плотностью заряда σ, модуль вектора напряженности электрического поля изменяется скачком нa E = σ / ε0.
208

Г л а в а 1 6
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ
Диэлектриками называют вещества, которые при обычных условиях практически не проводят электрический ток. В диэлектриках нет свободных носителей зарядов — заряженных частиц, которые под действием электрического поля могли бы прийти в упорядоченное движение и создать электрический ток проводимости. К диэлектрикам относятся все газы (если они не подверглись ионизации), некоторые жидкости и твердые тела. Удельное электрическое сопро-
тивление диэлектриков ρ ≈ 106…1015 Омæм, тогда как у металлов
ρ ≈ 10– 8…10– 6 Омæм. Особенности поведения диэлектриков в электростатических полях объясняются прежде всего их молекулярным строением. Электрически заряженные элементарные частицы, входящие в состав молекул диэлектриков, достаточно прочно связаны одна с другой внутриатомными силами. Электрические заряды частиц, входящих в состав атомов и молекул, а также заряды ионов в кристаллических диэлектриках с ионной решеткой, называются связанными зарядами. Заряды частиц, не входящих в состав атомов и молекул вещества, называются свободными. Это заряды частиц, способных перемещаться под действием электрического поля (свободные электроны в металлах и полупроводниках, ионы в электролитах и газах, электроны и ионы в плазме), положительные заряды ионов кристаллической решетки металлов, избыточные заряды, сообщенные проводящему телу. Рассмотрение поведения диэлектриков в электростатических полях мы начнем с изучения характеристик связанных зарядов.
16.1. Диполь в электростатическом поле. Поляризация диэлектриков. Типы диэлектриков
Все молекулы диэлектрика электрически нейтральны: суммарный заряд электронов и атомных ядер в составе молекул равен нулю. Но молекула обладает электрическими свойствами: ее можно рассмат-
ривать как электрический диполь с дипольным моментом º = º , p q l
º
где q — положительный заряд всех атомных ядер молекулы, а l — вектор, проведенный из «центра тяжести» электронного облака в
209
|
M |
q |
F+ |
|
l |
+ |
|
|
|
|
|
F– |
|
|
E |
– |
|
||
|
|
|
|
|
–q |
|
x |
|
|
|
Рис. 16. 1
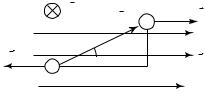
молекуле в «центр тяжести» положительных зарядов атомного ядра (рис. 16.1).
Рассмотрим поведение молекулярного диполя в однородном электрическом поле. На заряды диполя в поле будет действовать пара сил:
º |
|
º |
|
º |
º |
|
|
F+ |
= q E |
; |
F– |
= – q E |
, |
||
причем |
|
|
|
|
|
|
|
|
|
|
|
º |
|
|
|
|
º |
|
|
|
|
|
|
|
F+ |
= |
F– |
|
= qE . |
(16.1) |
|
Возникшая пара сил, действуя совместно на заряды диполя, будет создавать вращающий момент M = M+ + M– = qEl sin α = pE sin α;
направление вектора |
º |
указано на рис. 16.1 (он перпендикулярен |
||||||
M |
||||||||
плоскости рисунка). В векторном виде |
|
|||||||
|
|
º |
|
|
º |
|
|
|
|
|
º |
|
. |
(16.2) |
|||
|
|
M = |
|
p , |
E |
|||
|
|
|
|
|
|
|
|
|
Действие момента сил будет приводить к повороту диполя таким образом, чтобы направления векторов дипольного момента и напряженности электрического поля совпали.
Этот же результат можно получить из энергетических представлений. Суммарная потенциальная энергия зарядов диполя
W = W+ + W– = qϕ+ – qϕ– = q (ϕ+ – ϕ– ),
где ϕ+ и ϕ– — потенциалы точек расположения положительного и
отрицательного заряда диполя соответственно. Учитывая связь напряженности поля и разности потенциалов (15.14) для однородного поля, получаем W = – pE cos α.
Действие электрических сил приводит диполь в состояние устойчивого равновесия, когда его потенциальная энергия минимальна,
º |
º |
т.е. cos α = 1, α = 0, p |
|| E . |
При внесении диполя в неоднородное электрическое поле, напряженность которого в разных точках пространства различна, силы, действующие на заряды диполя, будут не равны одна другой:
210
