5. Непараметрические методы анализа.

Как мы изучили на предыдущих занятиях, для изучения тесноты связи между Х и У используется коэффициент (индекс) корреляции.

В некоторых случаях мы можем встретиться с такими качествами, которые не поддаются выражению числом единиц.

Эти обстоятельства заставляют прибегать к использованию т. н. непараметрических методов, позволяющих измерить интенсивность связи как между количественными признаками, так и между качественными.

При исследовании тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффици­енты ассоциации (Ка) и контингенции (Кк) . Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каж­дое из которых должно быть альтернативным, т. е. состоящим из двух качественно отличных друг от друга значений признака (табл. 8).

Таблица 8

Таблица для вычисления коэффициентов ассоциации и контингенции

a	b	a + b
с	d	с + d
а + с	b + d	a+b+с+d

Коэффициенты вычисляются по формулам:

ассоциации:

контингенции:

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если Ка > 0,5 или К_к>0,3.

Пример 1: Оцените наличие связи между студентами группы, распределённых по полу, и заинтересованностью их предметом «Статистика» (табл. 9), рассчитав Ка и Кк. (Данные получаем на основании опроса, проведенного в классе.)

Таблица 9

Статистика, как предмет изучения	Пол		Всего
	Мужской	Женский
Интересный	3	15	18
Неинтересный	2	15	17
Итого	5	30	35

Ка = Кк =

Вывод: Т. к. Ка < 0,5 и Кк < 0,3 то заинтересованность статистикой не зависит от пола студентов.

Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно при­менение коэффициентов взаимной сопряженности Пирсона и Чупрова, которые вычисляются по следующим формулам:

; ,

Где:

- показатель взаимной сопряжённости;

- определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки минус 1:

,

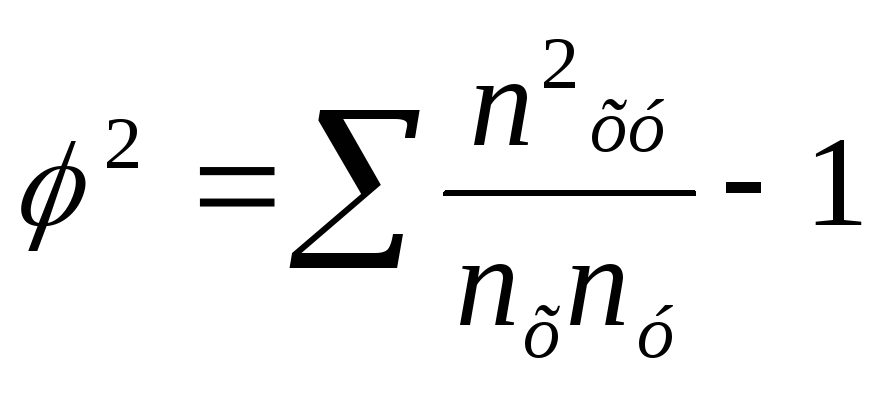где К₁- число значений (групп) первого признака

К₂- число значений (групп) второго признака

Чем ближе Кп и Кч, тем связь теснее.

Таблица 10

Вспомогательная таблица для расчёта коэффициента взаимной сопряжённости

Х У	I	I I	I I I	Всего
I	…	…	nху	nх
I I	…	…		nх
I I I	…	…		nх
Итого	nу	nу	nу	n

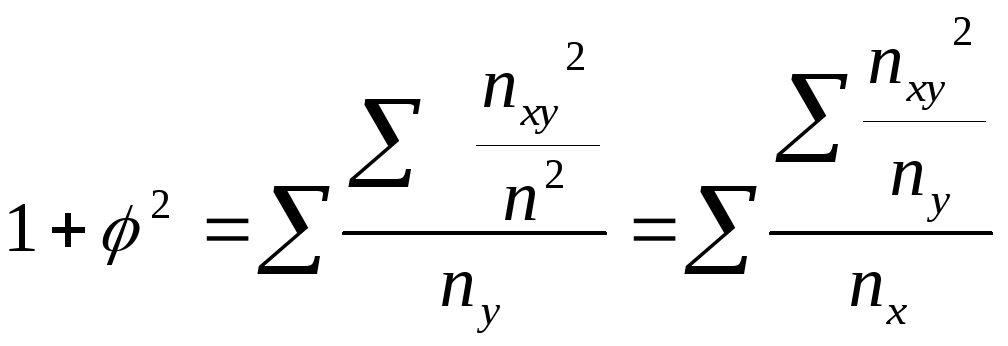
Пример 2. Оцените зависимость освоения курса «Статистика» от типа школы, которую окончили студенты данной группы (табл. 11) (исходные данные получаем путём опроса студентов группы непосредственно на занятии).

Таблица 11

Зависимость освоения «Статистики» от типа школы, которую закончили студенты

Тип школы	Освоение курса «Статистика»			Итого
	Хорошее	Среднее	Плохое
Лицей, гимназия, специализированные школы, классы	5	2	3	10
Общеобразовательная городская школа	5	6	9	20
Общеобразовательная сельская школа	2	1	2	5
Итого	12	9	14	35

Решение: Кп =;

1 + =+

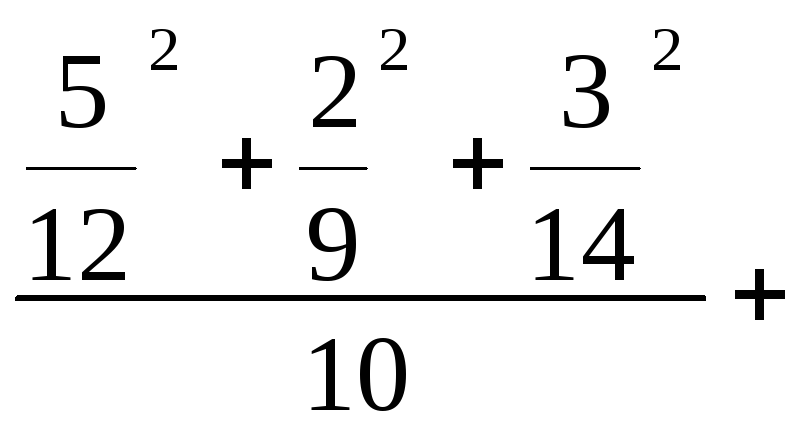
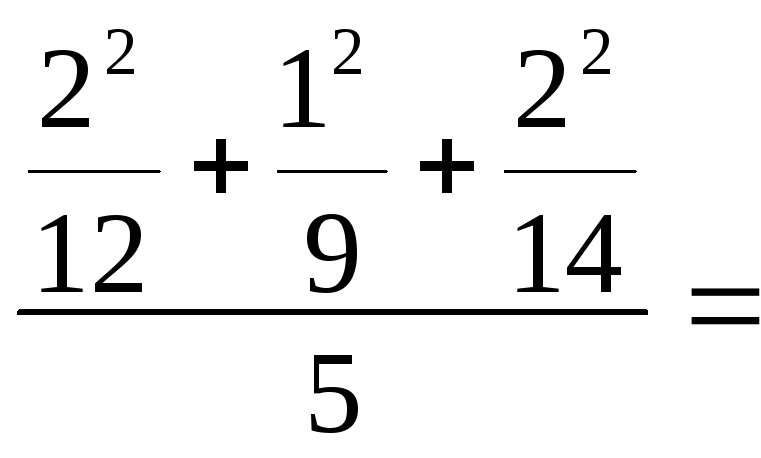
+0,316+0,693+0,146=1,055

= 1,055-1=0,055

Кп ==0,228

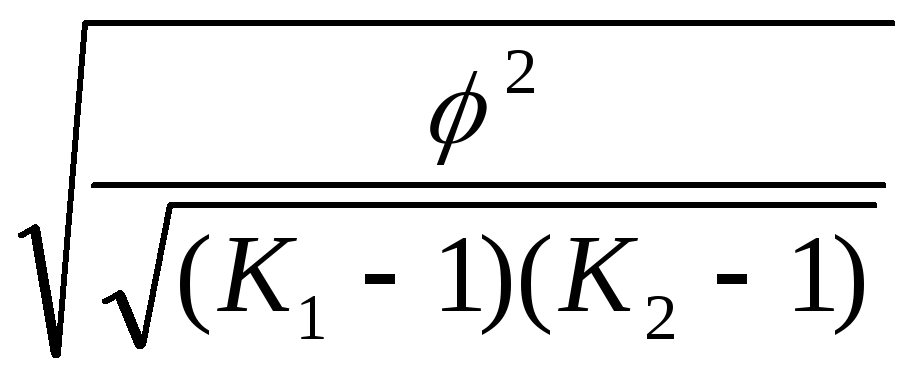Кч = ==0,164

Чем Кп и Кч ближе к 1, тем связь сильнее.

Вывод: Освоение курса «Статистика» не зависит от типа школы, которую закончили студенты.

Для определения тесноты связи как между количественными, так и между качественными признаками при условии, что значения этих признаков могут быть упорядочены (проранжированы) по степени убывания или возрастания признака используют коэффициент корреляции рангов Спирмена, который рассчитывается по формуле:

,

где d_i – квадраты разности величин x и y.

n - число наблюдений (число пар рангов)

Используя данные примера 2 по нелинейной корреляционной зависимости, рассчитаем коэффициент Спирмена. Для этого построим таблицу 12.

Таблица 12