
- •1. Причинность, регрессия, корреляция.
- •Корреляционно – регрессионный анализ. Линейная парная регрессия.
- •Оценка линейного коэффициента корреляции
- •Шкала Чеддока
- •Показатели работы некоторых сельскохозяйственных предприятий Тамбовской области (данные условные)
- •Расчетная таблица
- •Нелинейная парная корреляция.
- •Производство и себестоимость продукции на одном из заводов Тамбовской области в 2011 году
- •Расчетная таблица
- •4. Множественная регрессия.
- •Исходные данные
- •Расчётная таблица
- •5. Непараметрические методы анализа.
- •Вспомогательная таблица для расчёта коэффициента взаимной сопряжённости
- •Зависимость освоения «Статистики» от типа школы, которую закончили студенты
- •Расчётная таблица
- •Расчётная таблица
- •Расчетная таблица
Расчётная таблица
|
№ п/п |
У |
Х1 |
Х2 |
У2 |
Х12 |
Х22 |
Х1Х2 |
Х1У |
Х2У |
|
1 |
- 6,4 |
6,3 |
36,1 |
40,96 |
39,69 |
1303,21 |
227,43 |
-40,32 |
-231,04 |
|
2 |
- 8,4 |
4,0 |
32,1 |
70,56 |
16,00 |
1030,41 |
128,40 |
-33,60 |
-269,64 |
|
3 |
- 2,9 |
7,7 |
42,4 |
8,41 |
59,29 |
1797,76 |
326,48 |
-22,33 |
-122,96 |
|
4 |
- 10,8 |
7,2 |
19,9 |
116,64 |
51,82 |
396,01 |
143,28 |
-77,76 |
-214,92 |
|
5 |
- 10,9 |
5,8 |
11,7 |
118,81 |
33,64 |
136,89 |
67,86 |
-63,22 |
-127,53 |
|
6 |
- 12,6 |
7,6 |
16,5 |
158,76 |
57,76 |
272,25 |
125,40 |
-95,76 |
-207,90 |
|
7 |
- 6,7 |
4,3 |
23,8 |
44,89 |
18,49 |
566,44 |
102,34 |
-28,81 |
-159,46 |
|
8 |
- 7,8 |
5,8 |
19,1 |
60,84 |
33,64 |
364,81 |
110,78 |
-45,24 |
-148,98 |
|
9 |
- 8,9 |
8,5 |
29,4 |
79,21 |
72,25 |
864,36 |
249,90 |
-75,65 |
-261,66 |
|
10 |
- 7,8 |
4,6 |
18,6 |
60,84 |
21,16 |
345,96 |
85,56 |
-35,88 |
-145,08 |
|
11 |
- 7,8 |
7,3 |
20,2 |
60,84 |
53,26 |
408,04 |
147,46 |
-56,94 |
-157,56 |
|
12 |
- 8,1 |
6,1 |
16,7 |
65,61 |
37,21 |
278,89 |
101,87 |
-49,41 |
-135,27 |
|
13 |
- 6,8 |
4,0 |
16,1 |
46,24 |
16,00 |
259,21 |
64,40 |
-27,20 |
-109,48 |
|
14 |
- 9,0 |
4,9 |
16,3 |
81,0 |
24,01 |
265,59 |
79,87 |
-44,10 |
-146,70 |
|
15 |
- 8,3 |
5,7 |
21,1 |
68,89 |
32,49 |
445,21 |
120,27 |
-47,31 |
-175,13 |
|
16 |
- 11,7 |
4,0 |
18,5 |
136,89 |
16,00 |
342,25 |
74,00 |
-46,80 |
-216,45 |
|
17 |
- 10,7 |
4,0 |
20,1 |
114,49 |
16,00 |
401,01 |
80,40 |
-42,80 |
-215,07 |
|
18 |
9,8 |
5,2 |
26,0 |
96,04 |
27,04 |
676,00 |
135,20 |
50,96 |
254,80 |
|
19 |
- 6,.1 |
6,2 |
16,5 |
37,21 |
38,44 |
272,25 |
102,30 |
-37,82 |
-100,65 |
|
20 |
- 8,1 |
4,9 |
20,2 |
65,61 |
24,01 |
408,04 |
98,98 |
-39,69 |
-163,62 |
|
21 |
- 5,8 |
3,6 |
17,0 |
33,64 |
12,96 |
289,00 |
61,20 |
-20,88 |
-98,60 |
|
22 |
- 8,1 |
4,2 |
16,5 |
65,61 |
17,64 |
272,25 |
69,30 |
-34,02 |
-133,65 |
|
23 |
- 7,6 |
3,4 |
25,7 |
57,76 |
11,56 |
660,49 |
87,38 |
-25,84 |
-195,32 |
|
24 |
- 6,8 |
4,8 |
29,0 |
46,24 |
23,04 |
841,00 |
139,20 |
-32,64 |
-197,20 |
|
25 |
- 8,6 |
5,4 |
15,3 |
73,96 |
29,16 |
234,09 |
82,62 |
-46,44 |
-131,58 |
|
26 |
- 2,8 |
6,7 |
15,1 |
7,84 |
44,89 |
228,01 |
101,17 |
-18,76 |
-42,28 |
|
27 |
- 4,2 |
5,3 |
18,9 |
17,64 |
28,09 |
357,21 |
100,17 |
-22,26 |
-79,38 |
|
28 |
- 6,1 |
5,6 |
15,5 |
37,21 |
31,36 |
240,25 |
86,80 |
-34,16 |
-94,55 |
|
29 |
- 4,8 |
4,2 |
23,0 |
23,04 |
17,64 |
529,00 |
96,60 |
-20,16 |
-110,40 |
|
30 |
- 5,5 |
5,0 |
16,8 |
30,25 |
25,00 |
282,24 |
84,00 |
-27,50 |
-92,40 |
|
31 |
- 3,3 |
4,3 |
21,3 |
10,89 |
18,49 |
453,69 |
91,59 |
-14,19 |
-70,29 |
|
32 |
- 5,5 |
5,0 |
24,6 |
30,25 |
25,00 |
605,16 |
123,00 |
-27,50 |
-135,30 |
|
Итого |
-188,3 |
171,6 |
680,0 |
1967,07 |
973,03 |
15826,98 |
3695,21 |
-1184,03 |
-4435,25 |
|
Сред-няя |
- 5,9 |
5,4 |
21,2 |
64,5 |
30,4 |
494,593 |
115,475 |
-37,001 |
-138,601 |
Из второго уравнения вычтем первое, а из третьего – второе, получим:
-8,6441а2=1,9477
а2 = - 0,2253
Величину параметра а1 определим из следующего уравнения:
![]()
0,2496а1 + 0,2839 ·(- 0,2253) = - 1,0155
0,2496а1 - 0,0640 = - 1,0155
0,2496а1 = -1,0155 + 0,0640
а1 = - 0,9515: 0,2496
а1 = - 3,8121
Величину параметра а0 определим из следующего уравнения:
![]()
а0 + 5,4341 · (- 3,8121) + 23,275 · (- 0,2253) = - 6,5224
а0 - 20,7153 – 5,2439 = - 6,5224
а0 = - 6,5224 + 20,7153 + 5,2439
а0 = 19,4368
Таким образом, получаем уравнение, выражающее корреляционную зависимость между численностью безработных, численностью занятых в условиях, не отвечающих санитарным нормам, и естественным приростом (убылью) населения в расчёте на 1000 жителей в анализируемых областях:
Ух1х2 = 19,4368 - 3,8121х1 – 0,2253х2
В данном уравнении регрессии параметр а0 = 19,4368 показывает усреднённое влияние на результативный признак неучтённых (невыделенных для исследования) факторов; параметр а1 = - 3,8121 – коэффициент регрессии, который показывает, что с увеличением численности безработных на 1% - естественный прирост (убыль) населения в расчёте на 1000 жителей уменьшается на 3,8 человека; параметр а2 = - 0,2253 – коэффициент регрессии, который показывает, что с увеличением численности занятых в условиях, не отвечающих санитарным нормам, на 1% - естественный прирост (убыль) населения в расчёте на 1000 жителей уменьшается на 0,2 человека.
г) Вычислим
коэффициенты парной корреляции
![]() ,
,
![]() ,
,
![]()
![]() найдём
по формуле:
найдём
по формуле:
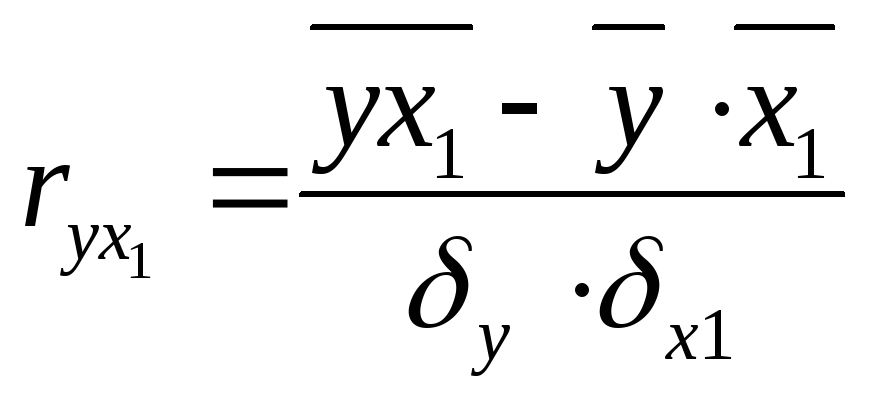 , где
, где
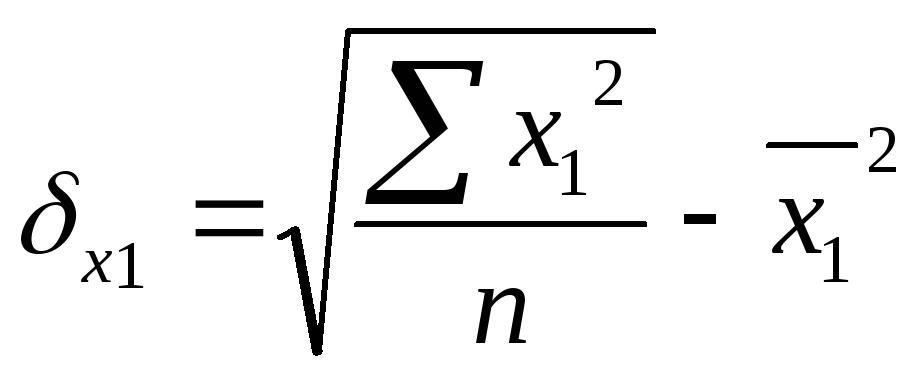
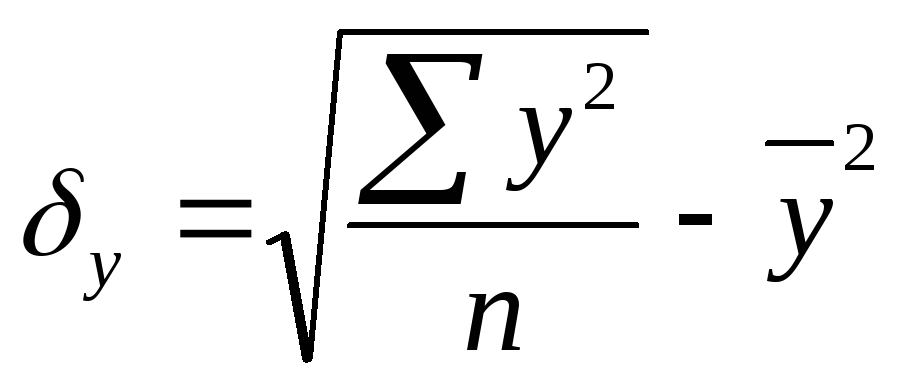
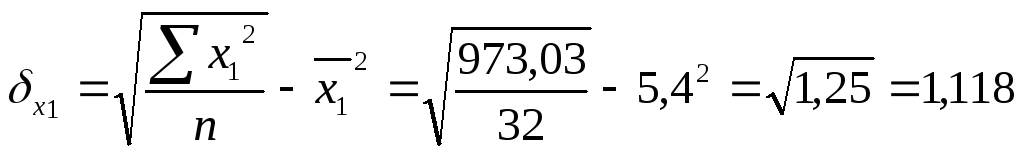
![]()
![]()
![]() найдём
по формуле:
найдём
по формуле:
 , где
, где
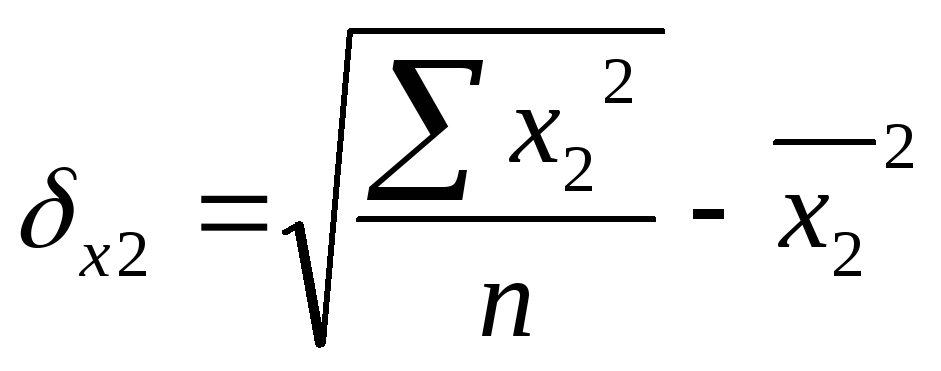
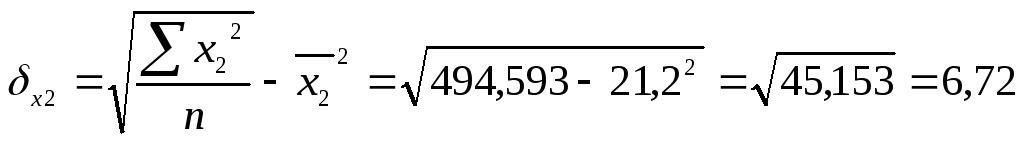
![]()
![]() найдём по формуле:
найдём по формуле:
![]()
Вычисленные коэффициенты парной корреляции показывают тесноту связи между численностью безработных, численностью занятых в условиях, не отвечающих санитарным нормам, и естественным приростом (убылью) населения в расчёте на 1000 жителей в анализируемых областях. Так,
![]() =
- 0,884 показывает, что между
численностью
безработных (Х1)
и естественным приростом (убылью)
населения в расчёте на 1000 жителей в
нашей задаче наблюдается высокая (по
шкале Чеддока), обратная (т. к. знак «-»)
зависимость, т. е. с ростом численности
безработных естественный прирост
уменьшается.
=
- 0,884 показывает, что между
численностью
безработных (Х1)
и естественным приростом (убылью)
населения в расчёте на 1000 жителей в
нашей задаче наблюдается высокая (по
шкале Чеддока), обратная (т. к. знак «-»)
зависимость, т. е. с ростом численности
безработных естественный прирост
уменьшается.
![]() =
- 0,387 показывает, что между
численностью
занятых в условиях, не отвечающих
санитарным нормам (Х2)
и естественным приростом (убылью)
населения в расчёте на 1000 жителей
наблюдается умеренная (по шкале Чеддока),
обратная (т. к. знак «-») зависимость, т.
е. с ростом численности занятых в
условиях, не отвечающих санитарным
нормам, естественный прирост в
анализируемых областях уменьшается.
=
- 0,387 показывает, что между
численностью
занятых в условиях, не отвечающих
санитарным нормам (Х2)
и естественным приростом (убылью)
населения в расчёте на 1000 жителей
наблюдается умеренная (по шкале Чеддока),
обратная (т. к. знак «-») зависимость, т.
е. с ростом численности занятых в
условиях, не отвечающих санитарным
нормам, естественный прирост в
анализируемых областях уменьшается.
![]() =
0,132 показывает, что между
численностью
безработных (Х1)
и численностью занятых в условиях, не
отвечающих санитарным нормам (Х2),
наблюдается слабая (по шкале Чеддока),
прямая (т. к. знак «+») зависимость, т. е.
с ростом численности занятых в условиях,
не отвечающих санитарным нормам,
численность безработных увеличивается,
и, наоборот.
=
0,132 показывает, что между
численностью
безработных (Х1)
и численностью занятых в условиях, не
отвечающих санитарным нормам (Х2),
наблюдается слабая (по шкале Чеддока),
прямая (т. к. знак «+») зависимость, т. е.
с ростом численности занятых в условиях,
не отвечающих санитарным нормам,
численность безработных увеличивается,
и, наоборот.
д) Множественный коэффициент корреляции для двух факторных (Х1 и Х2) признаков вычисляется по формуле:
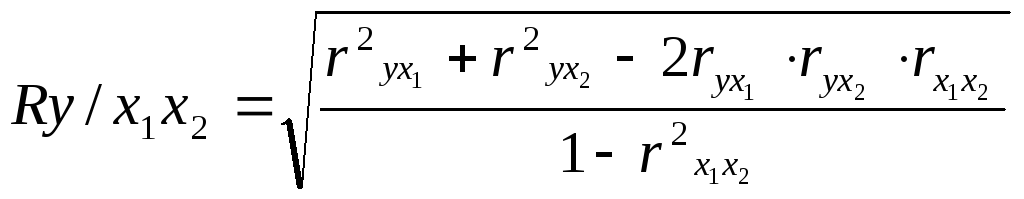 ,
где
,
где
rух - парные коэффициенты корреляции между признаками.
Следовательно, в нашей задаче, множественный коэффициент корреляции равен:
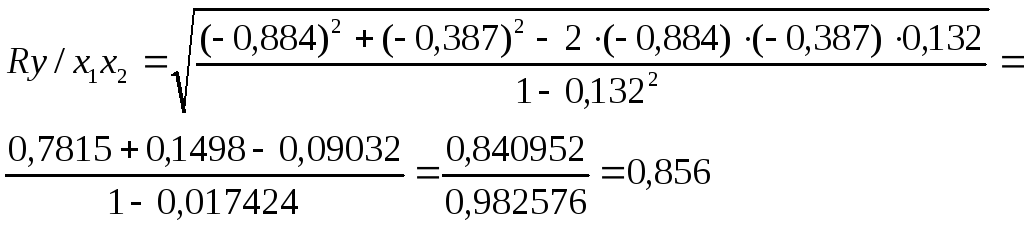
Коэффициент множественной корреляции изменяется в пределах от 0 до 1 и по определению положителен: 0 ≤ R ≤ 1.
Приближение R к единице свидетельствует о сильной зависимости между признаками.
Следовательно,
вычисленный коэффициент
множественной корреляции
![]() характеризует,
о том, что между
численностью
безработных, численностью занятых в
условиях, не отвечающих санитарным
нормам, и естественным приростом (убылью)
населения в расчёте на 1000 жителей в
анализируемых областях существует
сильная взаимосвязь.
характеризует,
о том, что между
численностью
безработных, численностью занятых в
условиях, не отвечающих санитарным
нормам, и естественным приростом (убылью)
населения в расчёте на 1000 жителей в
анализируемых областях существует
сильная взаимосвязь.
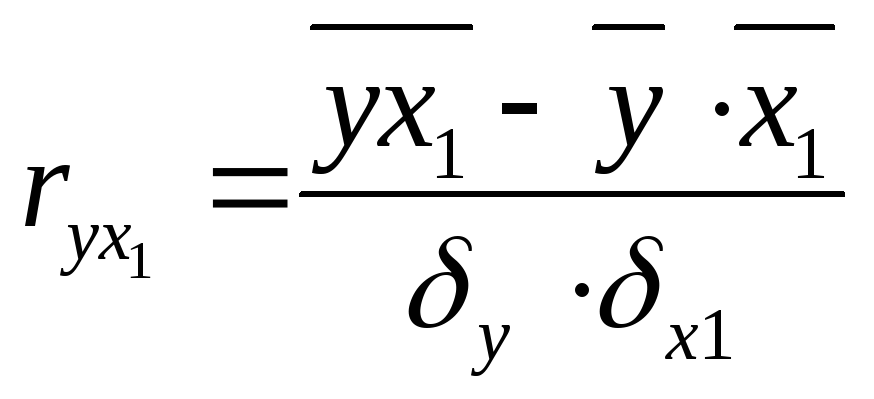
![]()
![]()
е) Вычислим частные коэффициенты корреляции, которые характеризуют степень тесноты связи между двумя признаками х1 и х2 при фиксированном значении других (k - 2) факторных признаков, то есть когда влияние х1 исключается, то есть оценивается связь между х1 и х2 в "чистом виде".
В случае зависимости у от двух факторных признаков х1 и х2 коэффициенты частной корреляции имеют вид:
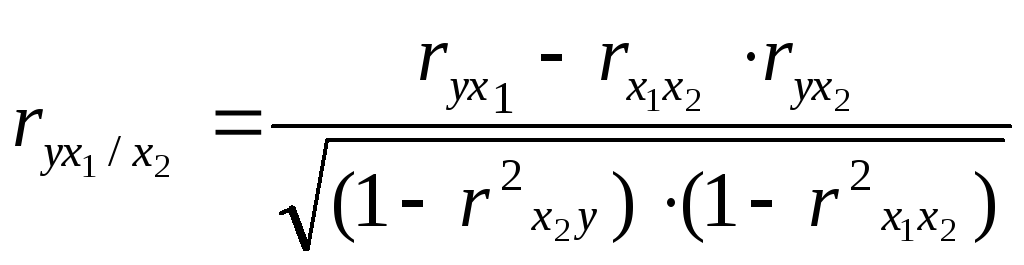
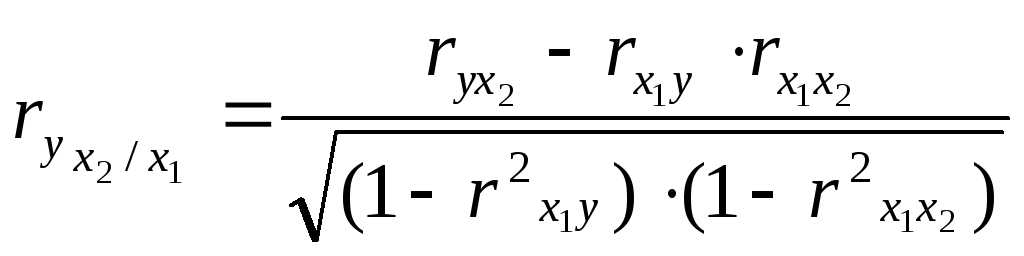 ,
,
где r – парные коэффициенты корреляции между указанными в индексе переменными.
В первом случае исключено влияние факторного признака х2, во втором – х1.
В нашей задаче:
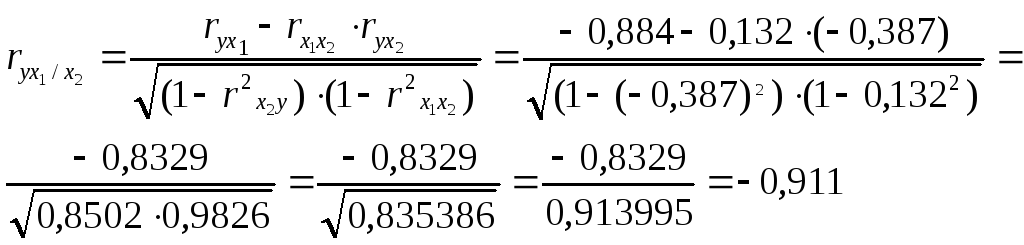
Значит, между численностью безработных (Х1) и естественным приростом (убылью) населения в расчёте на 1000 жителей (У) при фиксированном значении показателя Х2 наблюдается высокая (по шкале Чеддока), обратная (т. к. знак «-») зависимость.
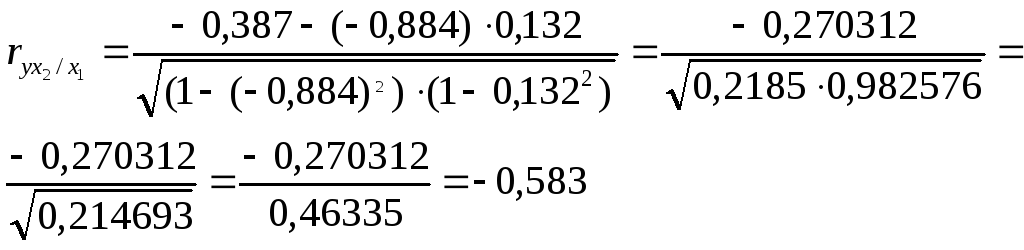
Следовательно, между численностью занятых в условиях, не отвечающих санитарным нормам (Х2), и естественным приростом (убылью) населения в расчёте на 1000 жителей (У) при фиксированном значении показателя Х1 наблюдается заметная (по шкале Чеддока), обратная (т. к. знак «-») зависимость.
