3. Нелинейная парная корреляция.

Пример 2. Используя данные таблицы 4, выявите характер связи между факторными и результативными признаками. Изобразите корреляционную связь графически. Измерьте тесноту связи с помощью коэффициента корреляции. Постройте адекватное уравнение регрессии, рассчитайте коэффициент Фишера и ошибку аппроксимации.

Таблица 4

Производство и себестоимость продукции на одном из заводов Тамбовской области в 2011 году

Месяцы	Произведено продукции, тыс. штук.	Себестоимость единицы продукции, руб.
	X	Y
1	0,5	25,0
2	2,0	19,8
3	3,1	19,0
4	2,5	19,5
5	5,8	17,2
6	1,8	20,1
7	3,4	18,0
8	12,0	15,2
9	8,3	15,4
10	6,0	15,8
11	5,4	16,6
12	7,2	17,1

По данным о себестоимости единицы продукции и объёма произведенной продукции определим направление и тесноту связи между признаками. Представим вышеприведенные данные в таблице 5 после предварительной их обработки методом приведения параллельных данных.

Сопоставив полученные ряды данных x и y можно наблюдать наличие обратной зависимости между признаками, когда увеличение объёма произведенной продукции ведёт к снижению себестоимости единицы продукции. Исходя из этого, можно сделать предположение, что связь между признаками обратная, и ее можно описать уравнением гиперболы. Этот же вывод подтверждается и на основе графического анализа (рис.2).

Анализ рис.2 показывает наличие близкой к криволинейной зависимости, так как точки расположены по кривой линии – допустим, что это гипербола.

Уравнение гиперболы:

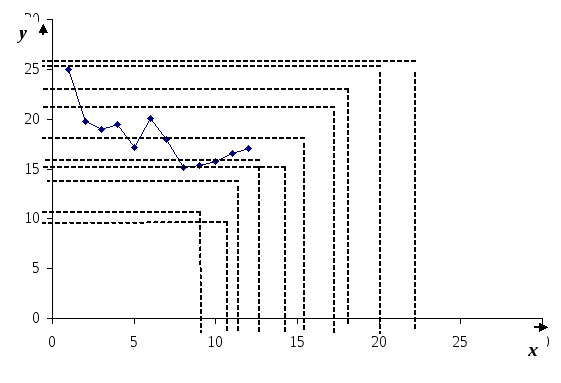
Рис. 2. Зависимость себестоимости единицы продукции от

объёма произведенной продукции.

Определим параметры уравнения гиперболы на основе метода наименьших квадратов. Исходные данные и расчетные показатели представлены в таблице 5.

Систему нормальных уравнений для нахождения параметров гиперболы можно представить следующим образом:

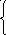
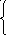
–Из первого уравнения вычитаем второе.

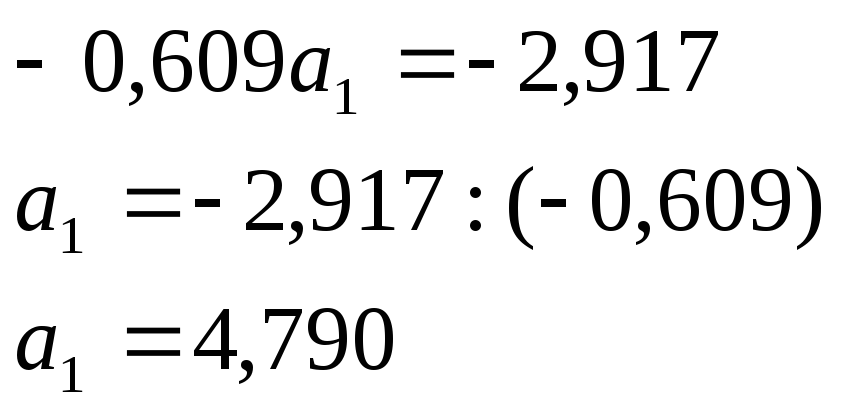
Далее

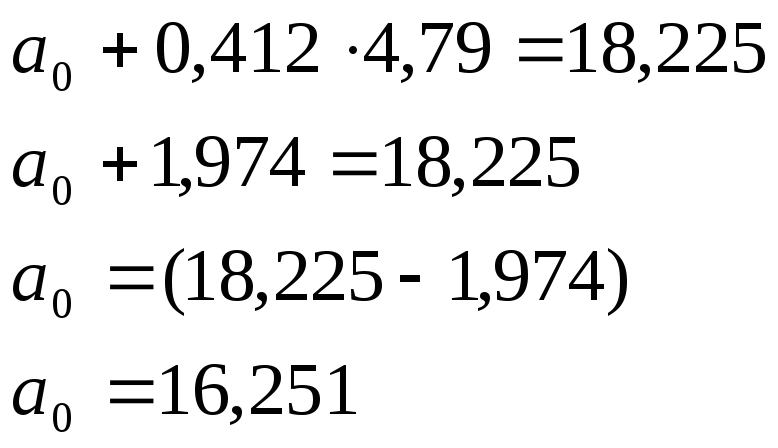
Уравнение гиперболы:

Отсюда:

(19)

В уравнении регрессии а₁ = 4,79 – коэффициент регрессии показывает, что с увеличением производства продукции на 1 тыс. штук, себестоимость продукции сокращается на 4,79 руб.

Проверим параметры данного уравнения на типичность. Для этого, используя формулы (3), (4), (5), (6), рассчитаем необходимые данные.

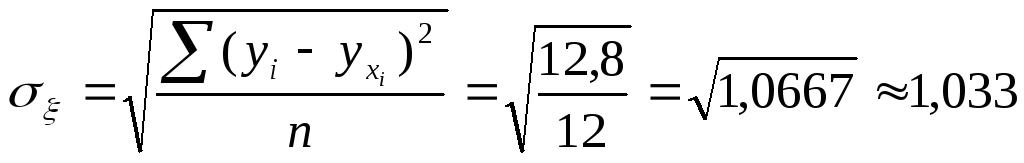
На основании выявленной модели (19) определим теоретические (выровненные значения себестоимости в зависимости от количества произведенной продукции) и запишем в табл. 5 (гр. 7):

Таблица 5

Расчетная таблица

месяцы	Производство продукции, тыс. штук	Себестоимость единицы продукции, руб.						()2
1	2	3	4	5	6	7	8	9	10	11	12
1	0,5	25,0	2,0	4,0	50,0	25,83	-0,83	0,689	-4,33	18,75	0,033
2	1,8	20,1	0,556	0,309	11,137	18,91	1,19	1,416	-3,03	9,181	0,059
3	2,0	19,8	0,5	0,25	9,9	18,651	1,15	1,320	-2,83	8,009	0,058
4	2,5	19,5	0,4	0,16	7,8	18,17	1,33	1,769	-2,33	5,429	0,068
5	3,1	19,0	0,323	0,104	6,129	17,8	1,2	1,44	-1,73	2,993	0,063
6	3,4	18,0	0,294	0,087	5,294	17,66	0,34	0,116	-1,43	2,045	0,019
7	5,4	16,6	0,185	0,034	3,074	17,14	-0,54	0,292	0,57	0,325	0,033
8	5,8	17,2	0,173	0,030	2,966	17,08	0,12	0,014	0,97	0,941	0,007
9	6,0	15,8	0,167	0,028	2,633	17,05	-1,25	1,563	1,17	1,369	0,079
10	7,2	17,1	0,139	0,019	2,375	16,92	0,18	0,032	2,37	5,617	0,011
11	8,3	15,4	0,121	0,015	1,856	16,83	-1,43	2,045	3,47	12,041	0,093
12	12,0	15,2	0,083	0,007	1,276	16,651	-1,45	2,104	7,17	51,409	0,095
ИТОГО	58,0	218,7	4,941	5,043	104,461	218,69	х	12,800	х	118,109	0,618

Определим по специальным таблицам распределения Стьюдента (t – распределение) (v=n-k, где k – число фактических признаков; v= 12-1-1=10) (приложение 3) t_k = 2,228.

Сравнение фактических и табличных значений t – критерия:

49,75 > 2,228 < 46,0

позволяет признать вычисленные по уравнению (19) параметры типичными.

Далее произведем оценку практической значимости синтезированной модели (19). Для криволинейной связи оценка производится посредством индекса корреляции R по формуле (20):

,

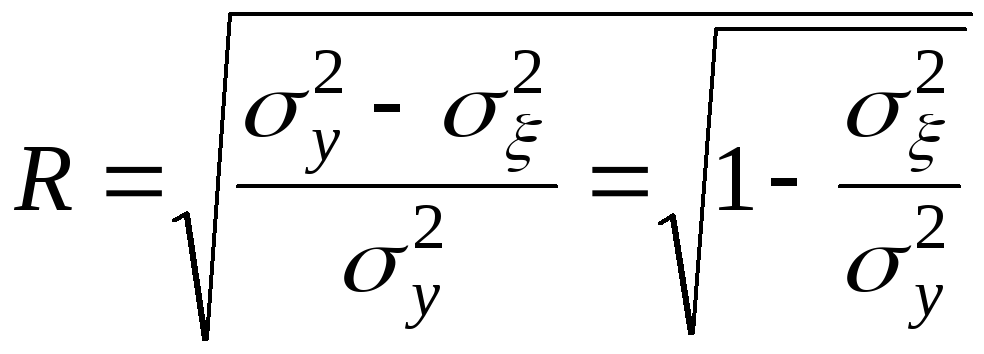где ,

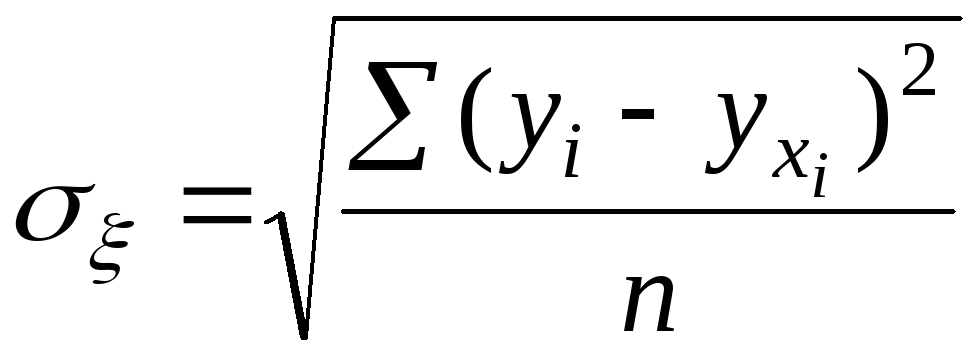
² = ;

Определяем индекс корреляции:

R = 0,919

Полученная величина R = 0,919 означает, что в соответствии со шкалой Чеддока установленная по уравнению регрессии связь между себестоимостью единицы продукции и объёмом произведенной продукции весьма высокая.

Оценка значимости коэффициента корреляции R = 0,919 осуществляется по F – критерию Фишера.

Фактическое значение критерия F_R определяется по формуле

(16)

где m – число параметров уравнения регрессии.

Величина F_R сравнивается с критическим значением F_k, которое определяется по таблице F-критерия с учетом принятого уровня значимости и числа степеней свободыk₂ = m – 1 (знаменатель) и k₂ = n – m (числитель).

При уровне значимости =0,5 и степенях свободыk₂ =2-1=1 и k_{1 =} 12 – 2 = 10, табличное значение Fk = 4,96. 54,35>4,96 , следовательно, величина индекса корреляции признается существенной.

R² – индекс детерминации = 0,919² =0,8446 или 84,5%. Отсюда следует, что 84,5% общей вариации объясняется изменением факторного признака Х.

Проверка адекватности всей модели осуществляется с помощью F-критерия и величины средней ошибки аппроксимации .

Значение средней ошибки аппроксимации определяется по формуле:

(17)

и не должно превышать 12-15%.

Среднюю ошибку аппроксимации определим по формуле (17)

Средняя ошибка аппроксимации составляет 11,0%.

Поэтому синтезированная по уравнению гиперболы математическая модель (19) может быть использована для практических целей.