Показатели работы некоторых сельскохозяйственных предприятий Тамбовской области (данные условные)

Номер предприятия	Фондовооруженность, тыс. руб.	Производительность труда, тыс. руб.
	X	Y
1	20,7	10,5
2	22,8	10,6
3	18,7	9,6
4	16,0	7,6
5	14,8	6,5
6	11,3	4,4
7	17,8	8,8
8	13,3	6,7
9	9,6	4,8
10	11,9	5,9

По данным о фондовооруженности и производительности труда в некоторых предприятиях области необходимо определить направление и тесноту связи между признаками. Данные в таблице 3 представлены после предварительной их обработки методом приведения параллельных данных. Сопоставив полученные ряды данных x и y можно наблюдать наличие прямой зависимости между признаками, когда увеличение фондовооруженности влечет за собой рост производительности труда. Исходя из этого, можно сделать предположение, что связь между признаками прямая, и ее можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа (рис.1).

Анализ рис.1 показывает наличие близкой к прямолинейной зависимости так как точки расположены практически по прямой линии.

Прямолинейная форма зависимости у от х описывается уравнением прямой:

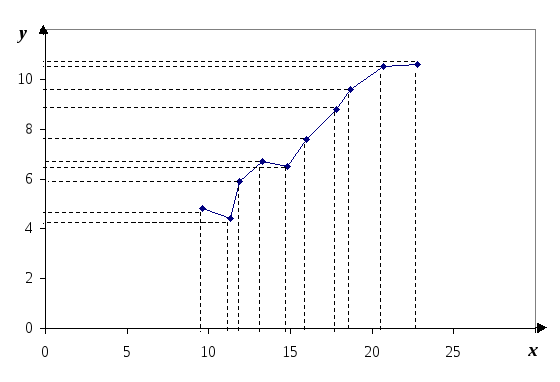
Рис. 1. Зависимость производительности труда в некоторых

сельскохозяйственных предприятиях области от

фондовооруженности, тыс. руб.

Определим параметры уравнения прямой на основе метода наименьших квадратов. Исходные данные и расчетные показатели представлены в таблице 3.

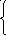
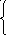
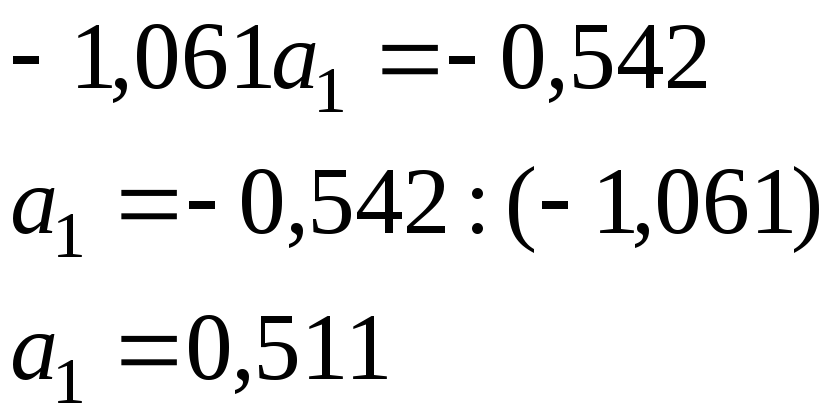
ТТаблица 3

Расчетная таблица

№ предприятия	Фондовооруженность, тыс. руб.	Производительность труда, тыс. руб.						()2
1	9,6	4,8	92,16	46,08	19,36	4,428	0,372	0,138	-6,09	37,008	0,078
2	11,3	4,4	127,69	49,72	23,04	5,296	-0,896	0,803	-4,39	19,272	0,204
3	11,9	5,9	141,61	70,21	34,81	5,603	0,297	0,088	-3,79	14,364	0,050
4	13,3	6,7	176,89	89,11	44,89	6,318	0,382	0,146	-2,39	5,712	0,057
5	14,8	6,5	219,04	96,2	42,25	7,085	-0,585	0,342	-0,89	0,792	0,09
6	16,0	7,6	256,0	121,6	57,76	7,698	-0,098	0,010	0,31	0,096	0,013
7	17,8	8,8	316,84	156,64	77,44	8,618	0,182	0,033	2,11	4,452	0,021
8	18,7	9,6	349,69	179,52	92,16	9,078	0,522	0,272	3,01	9,060	0,054
9	20,7	10,5	428,49	217,35	110,25	10,100	0,4	0,16	5,01	25,1	0,038
10	22,8	10,6	519,84	241,68	112,36	11,173	-0,573	0,328	7,11	50,552	0,054
Итого	156,9	75,4	2628,25	1268,11	614,32	75,397	-	2,32	-	166,488	0,659

Далее

Уравнение прямой:

Отсюда:

(18)

Параметры уравнения а₀ и а₁ можно также вычислить по следующим формулам

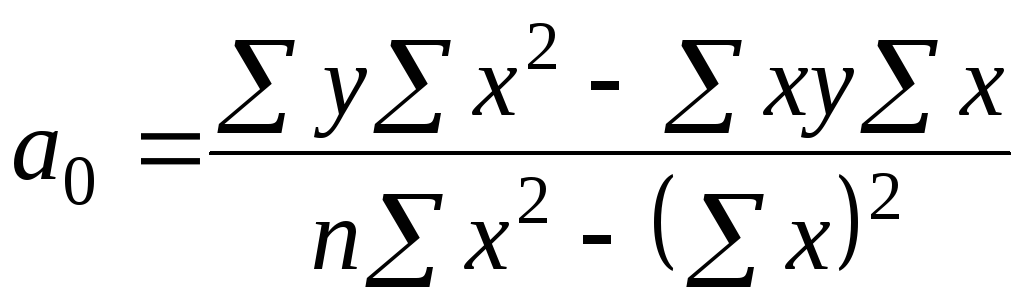
В уравнении регрессии параметр а₀ показывает усреднённое влияние на результативный признак неучтённых (невыделенных для исследования) факторов; параметр а₁ = 0,511 – коэффициент регрессии показывает, что с увеличением фондовооруженности труда на 1 тыс. рублей, производительность труда возрастает на 0,511 тыс. руб.

Проверим параметры данного уравнения на типичность. Для этого, используя формулы (3), (4), (5), (6), рассчитаем необходимые данные.

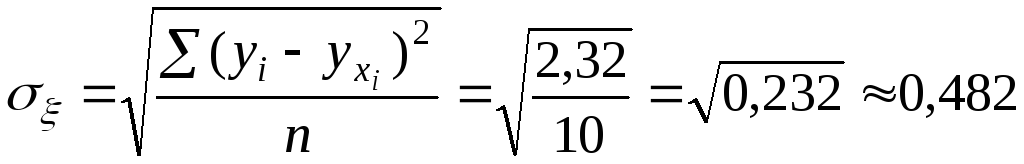
Определим по специальным таблицам распределения Стьюдента (t – распределение) (приложение № 1) t_k = 2,306.

Сравнение фактических и табличных значений t – критерия:

- 2,805 > 2,306 < 12,232

позволяет признать вычисленные по уравнению параметры:

а₀ – нетипичным, а₁ - типичным.

Далее произведем оценку практической значимости синтезированной модели . Для прямолинейной связи это выполняется посредством показателя коэффициента корреляции r. По формуле: определяем значениеr.

Полученная величина r = 0,974 означает, что в соответствии со шкалой Чеддока (стр. 147 данного пособия) установленная по уравнению регрессии связь между фондовооруженностью и производительностью труда весьма высокая.

Оценка значимости коэффициента корреляции осуществляется по t – критерию.

Фактическое значение этого критерия t_r определяется по формуле :

При критическом значении t_k =2,306 получается, что t_r > t_k. Поэтому вычисленный коэффициент корреляции признается существенным.

Среднюю ошибку аппроксимации определили по формуле:

Средняя ошибка аппроксимации составляет 6,6%.

Из значения r² = 0,974² = 0,949 следует, что 94,9% общей вариации объясняется изменением факторного признака.

Коэффициент эластичности определим по формуле:

,

где - среднее значение соответствующего факторного признака;

- среднее значение результативного признака;

a_i - коэффициент регрессии при соответствующем факторном признаке.

Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%.

Таким образом, построенная нами модель зависимости У от Х на основе ее проверки по t-распределению Стьюдента в целом адекватна, но не все коэффициенты регрессии значимы (а₀ – нетипичен). Такая модель может быть использована для практических целей, но не для осуществления прогнозов.