
первая лаба
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО «Чувашский государственный университет
имени И.Н.Ульянова»
Электротехнический факультет
Кафедра электрических и электронных аппаратов
Отчет по лабораторной работе №1
МОДЕЛИРОВАНИЕ МАГНИТНИТНЫХ ПРОВОДИМОСТЕЙ
ВОЗДУШНЫХ ПРОМЕЖУТКОВ ЭЛЕКТРОМАГНИТНЫХ СИСТЕМ
Вариант №6
Выполнила студент
группы ЭТ-21-10:
Гаврилов А.Ю
Проверила: Николаев Н.Н
Чебоксары 2013
Лабораторная работа 1
МОДЕЛИРОВАНИЕ МАГНИТНИТНЫХ ПРОВОДИМОСТЕЙ
ВОЗДУШНЫХ ПРОМЕЖУТКОВ ЭЛЕКТРОМАГНИТНЫХ СИСТЕМ
Цель работы – изучение основ работы с программой FEMM, моделирование безвихревого магнитного поля и магнитной проводимости воздушных промежутков магнитных цепей электромагнитных механизмов в среде FEMM.
Общие сведения
Расчет магнитных проводимостей воздушных промежутков – наиболее часто встречающаяся задача при проектировании электромагнитных систем электрических аппаратов. Точность расчета магнитных проводимостей во многом определяет точность расчета магнитной цепи, а значит и тяговых усилий электромагнита. Для расчета магнитных проводимостей в основном используются три метода: 1) на основании упрощающих предположений относительно картины магнитного поля – метод вероятных путей потока; 2) на основании математической обработки экспериментальных данных с применением методов теории подобия; 3) на основе расчета магнитного поля в рассматриваемой области. На практике первые два метода применяются чаще, однако они имеют существенные погрешности [1,2].
Третий
метод является наиболее строгим. Он
может обеспечить достаточно высокую
точность. Точность практически
ограничивается лишь ресурсами используемой
ЭВМ. В этом методе сначала рассчитывается
магнитное поле (значения магнитной
индукции
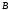 и напряженности магнитного поля
и напряженности магнитного поля
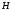 )
в воздушном промежутке между двумя
ферромагнитными поверхностями. Затем
по его характеристикам определяется
магнитная проводимость промежутка.
Понятие о магнитной проводимости
справедливо лишь для двух эквипотенциальных
поверхностей, имеющих соответственно
магнитные потенциалы
)
в воздушном промежутке между двумя
ферромагнитными поверхностями. Затем
по его характеристикам определяется
магнитная проводимость промежутка.
Понятие о магнитной проводимости
справедливо лишь для двух эквипотенциальных
поверхностей, имеющих соответственно
магнитные потенциалы
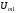 и
и
 ,
и пронизываемых одним и тем же магнитным
потоком Ф (рис. 1). При этом магнитная
проводимость Λ представляет собой
отношение
,
и пронизываемых одним и тем же магнитным
потоком Ф (рис. 1). При этом магнитная
проводимость Λ представляет собой
отношение
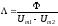 .
(1)
.
(1)
Кроме магнитной проводимости Λ, часто используется и обратная ей величина: магнитное сопротивление
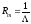 .
.
Магнитный поток, проходящий через одну из поверхностей, например S1, равен
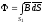 .
(2)
.
(2)
Такой же поток входит в поверхность S2.

Рис. 1. Магнитное поле в промежутке
между эквипотенциальными поверхностями
Разность магнитных
потенциалов находится в виде интеграла
по любому пути
 между эквипотенциальными поверхностями
между эквипотенциальными поверхностями
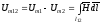 .
(3)
.
(3)
С учетом (2) и (3) из (1) получается магнитная проводимость в виде
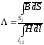 . (4)
. (4)
Таким образом, определение магнитной проводимости Λ сводится к расчету характеристик магнитного поля в промежутке между двумя элементами магнитной системы.
Магнитное поле в рассматриваемой области описывается системой уравнений Максвелла:
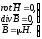 , (5)
, (5)
где
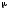 - абсолютная магнитная проницаемость
среды (воздуха)
- абсолютная магнитная проницаемость
среды (воздуха)
С учетом выражения для напряженности магнитного поля
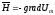
система уравнений (5) сводится к уравнению Лапласа:
 .
(6)
.
(6)
При этом на
поверхностях, образующих воздушный
промежуток, для составляющих векторов
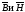 должны выполняться граничные условия:
должны выполняться граничные условия:
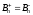 и
и
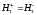 , (7)
, (7)
где
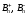 – соответственно нормальные составляющие
индукции магнитного поля в воздухе и
ферромагнетике;
– соответственно нормальные составляющие
индукции магнитного поля в воздухе и
ферромагнетике;
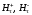 – касательные составляющие напряженности
магнитного поля для указанных областей.
Решение уравнения (6) с учетом граничных
условий (7) позволяет найти характеристики
магнитного поля в рассматриваемой
области.
– касательные составляющие напряженности
магнитного поля для указанных областей.
Решение уравнения (6) с учетом граничных
условий (7) позволяет найти характеристики
магнитного поля в рассматриваемой
области.
Уравнение Лапласа
(6) для магнитного поля может решаться
методом конечных разностей, но наиболее
эффективно оно решается методом вторичных
источников или методом конечных элементов
[1]. Для численного расчета магнитных
полей существуют достаточно большое
число компьютерных программ. Наиболее
доступной и адаптированной для расчетов
магнитных полей является специализированная
программа FEMM.
Программа FEMM
(Finite
Element
Method
Magnetics
– магнитные расчеты методом конечных
элементов) позволяет рассчитывать
параметры плоскопараллельных и
осесимметричных (плоскомеридианных),
т.е. двухмерных магнитных полей методом
конечных элементов (МКЭ). При этом
уравнение Лапласа (6) решается не
относительно скалярного магнитного
потенциала
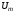 ,
а относительно векторного магнитного
потенциала
,
а относительно векторного магнитного
потенциала
 ,
связанного с магнитной индукцией
формулой
,
связанного с магнитной индукцией
формулой
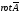 =
=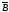 :
:
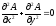 .
(8)
.
(8)
В плоскопараллельном
поле вектор
 имеет только одну составляющую,
направленную по оси OZ
имеет только одну составляющую,
направленную по оси OZ
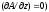 .
Это и упрощает решение уравнения Лапласа
МКЭ. Связь индукции
.
Это и упрощает решение уравнения Лапласа
МКЭ. Связь индукции
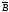 и векторного потенциала
и векторного потенциала
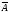 выражается формулой
выражается формулой
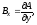
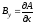 .
.
Программа FEMM для выполнения магнитных расчетов содержит три основные программы: препроцессор, процессор или решатель и постпроцессор. Препроцессор управляет построением модели и записывает ее в файл с расширением fem. Решатель рассчитывает параметры модели (магнитного поля) и сохраняет результаты расчета в файле с расширением ans. Постпроцессор для своих построений использует расчетные данные файла с расширением ans. Он строит и выводит на экран картины поля линий магнитного потока, кривые изменения различных параметров вдоль задаваемых пользователем линий.
Работа с программой FEMM при расчете магнитной проводимости в воздушном промежутке электромагнитных систем проводится в следующей последовательности [л.1: с. 191-226, 287-296]:
-
Предварительная подготовка (описание координат опорных точек).
-
Запуск программы FEMM и ввод типа задачи (магнитные проблемы, плоскопараллельная задача).
-
Построение контуров модели.
-
Ввод свойства блока.
-
Идентификация свойства блока.
-
Ввод граничных условий.
-
Идентификация граничных условий.
-
Построение конечно-элементной сетки и расчет модели.
-
Построение картин поля.
-
Построение графиков, расчеты и вывод на экран результатов расчета.
Задание
1. Изучить основы работы с программой FEMM при расчете параметров магнитного поля в воздушных промежутках магнитной цепи (л.1: с. 191-226, 287-296).
2. Построить модель воздушного промежутка по заданному варианту (л.1: с. 195-213, 287-291). Варианты даны в табл. 1 и на рис.1.
3. Построить сеть конечных элементов в заданном воздушном промежутке и рассчитать параметры магнитного поля в заданном воздушном промежутке (л.1: с. 213, 291-292).
4. Построить картины поля в воздушном промежутке (л.1: с. 214-218, 292-294).
5. Построить кривые изменения магнитной индукции вдоль линий поверхностей полюсов и плоскостей, образующих воздушный промежуток (л.1: с. 218-226, 294-295).
6. Рассчитать магнитное напряжение между полюсами (полюсом и плоскостью) по различным путям интегрирования (л.1: с. 218-226, 295-296).
7. Рассчитать магнитный поток в воздушном промежутке и определить удельную магнитную проводимость воздушного промежутка (л.1: с. 218-226, 295-296).
8. Исследовать зависимость удельной магнитной проводимости воздушного промежутка от длины стороны конечного элемента: lкэ=5; 1; 0,5; 0,1 мм. Построить зависимость удельной магнитной проводимости от lкэ.
9. Оформить отчет о лабораторной работе, который должен содержать:
- цель работы и задание;
- модель воздушного промежутка с указанием координат опорных точек;
- промежуточные рисунки и графики, иллюстрирующие выполненную работу;
- анализ результатов.
Таблица 1
Варианты заданий
|
№ п/п |
Вариант по рис. 1 |
Воздушный промежуток |
a, мм |
b, мм |
R, мм |
2α, град |
|
|
рис. 1, е |
Коническая призма – коническая призма |
15 |
40 |
- |
120 |
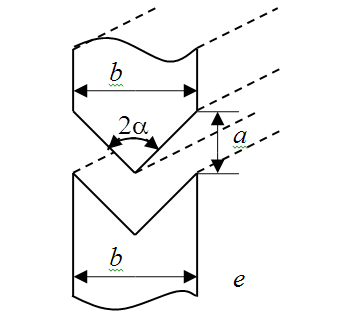
Рис. 1. Воздушные промежутки
между полюсом и плоскостью
и ферромагнитными полюсами
Выполнение
2.Находим
опорные точки, и строим модель воздушного
зазора.
E(0;45)
D(15;0)
А(0;0) C(20;0)
В(20;-15)
G(0;-30)
Рис.2 Модель воздушного промежутка
3.Построим сеть конечных элементов в заданном воздушном промежутке.
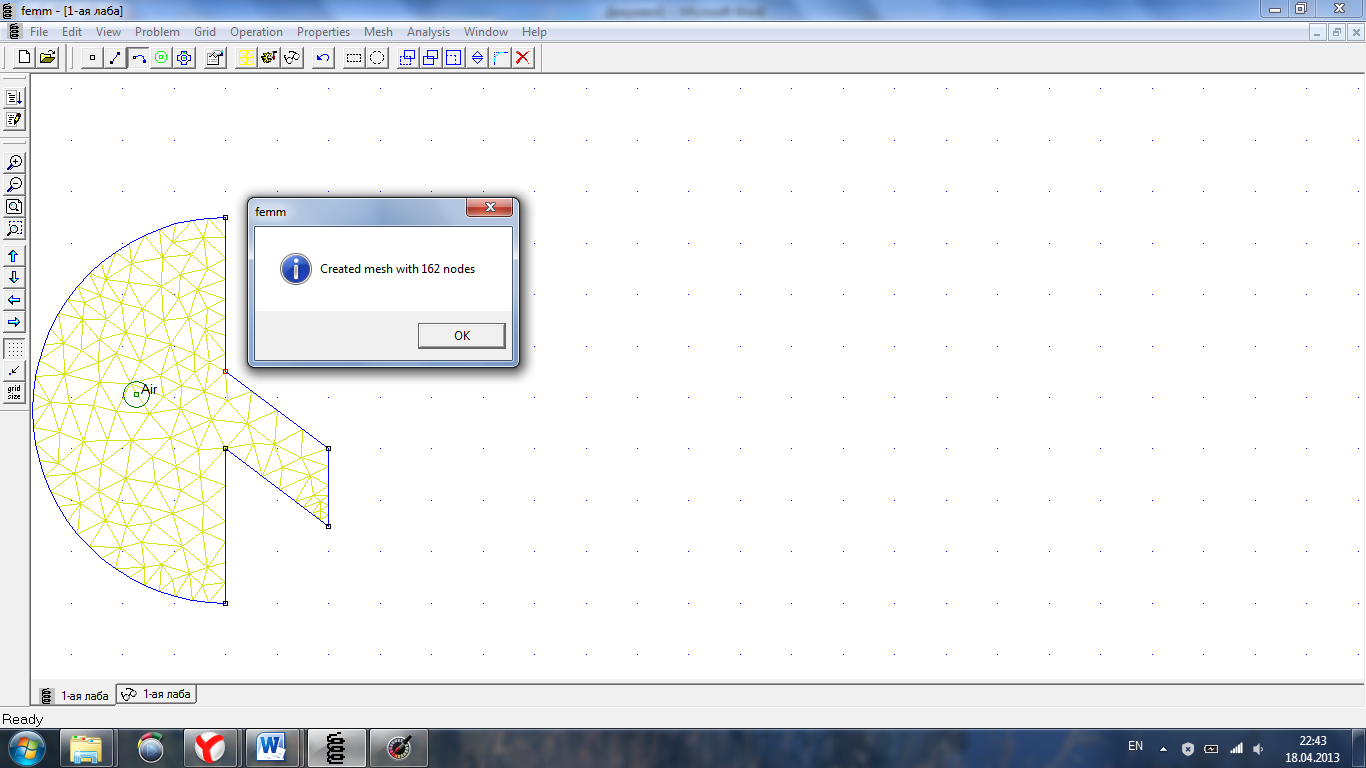
Рис.3 Сеть конечных элементов
4.Построим картину поля в воздушном промежутке.
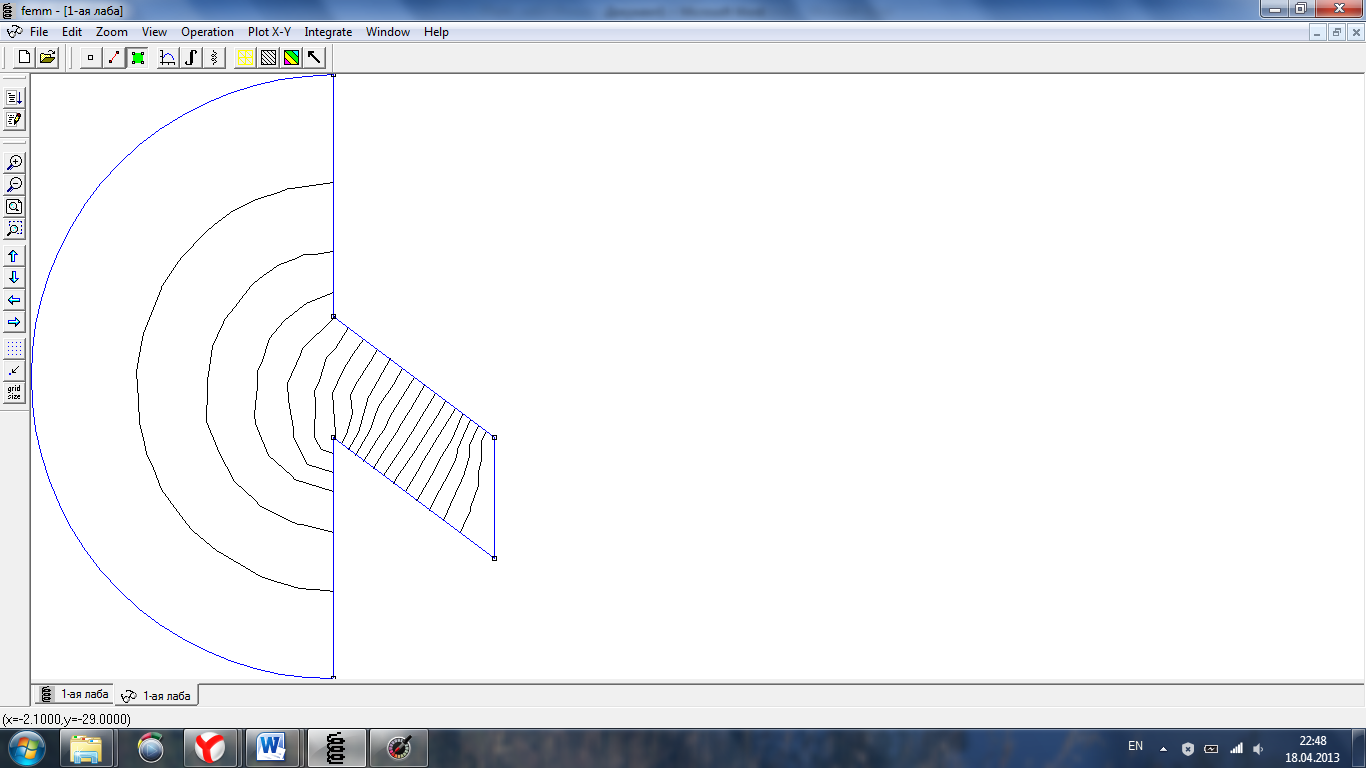
Рис.4 Картину поля линий потока
Выведем на экран зонную картину поля.

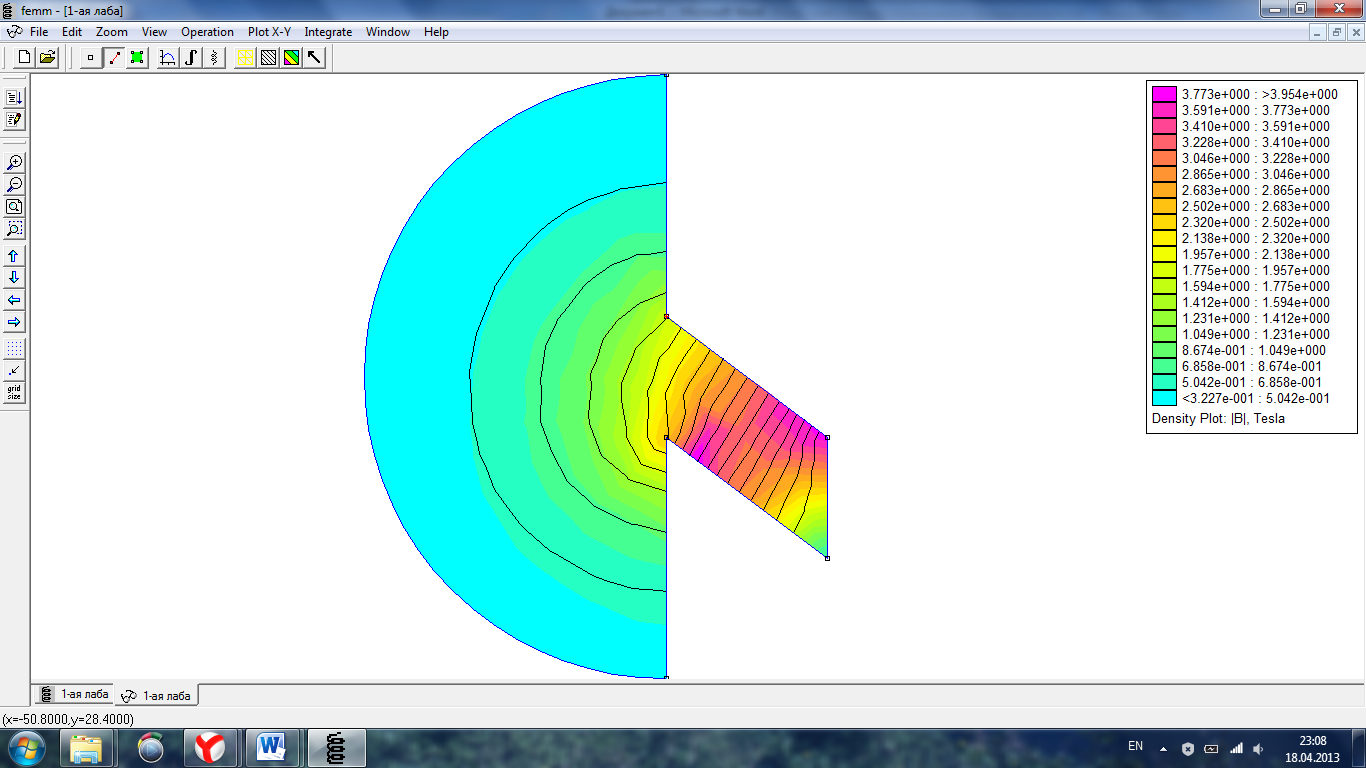
Рис.5 Зонная картина поля
Так-же покажем картину поля векторов магнитной индукции.
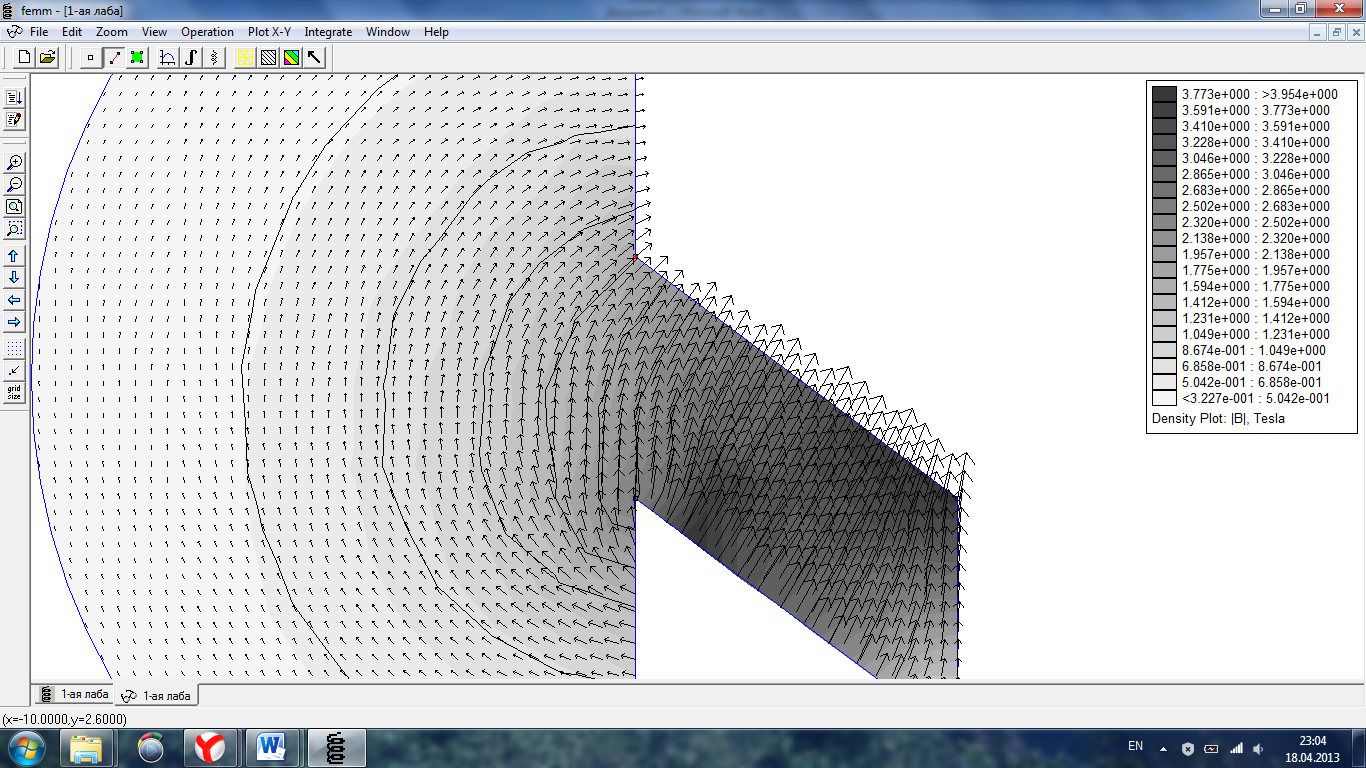
Рис.6 Картина поля векторов магнитной индукции.
5.Построим кривые изменения магнитной индукции вдоль линий поверхностей полюсов и плоскостей, образующих воздушный промежуток
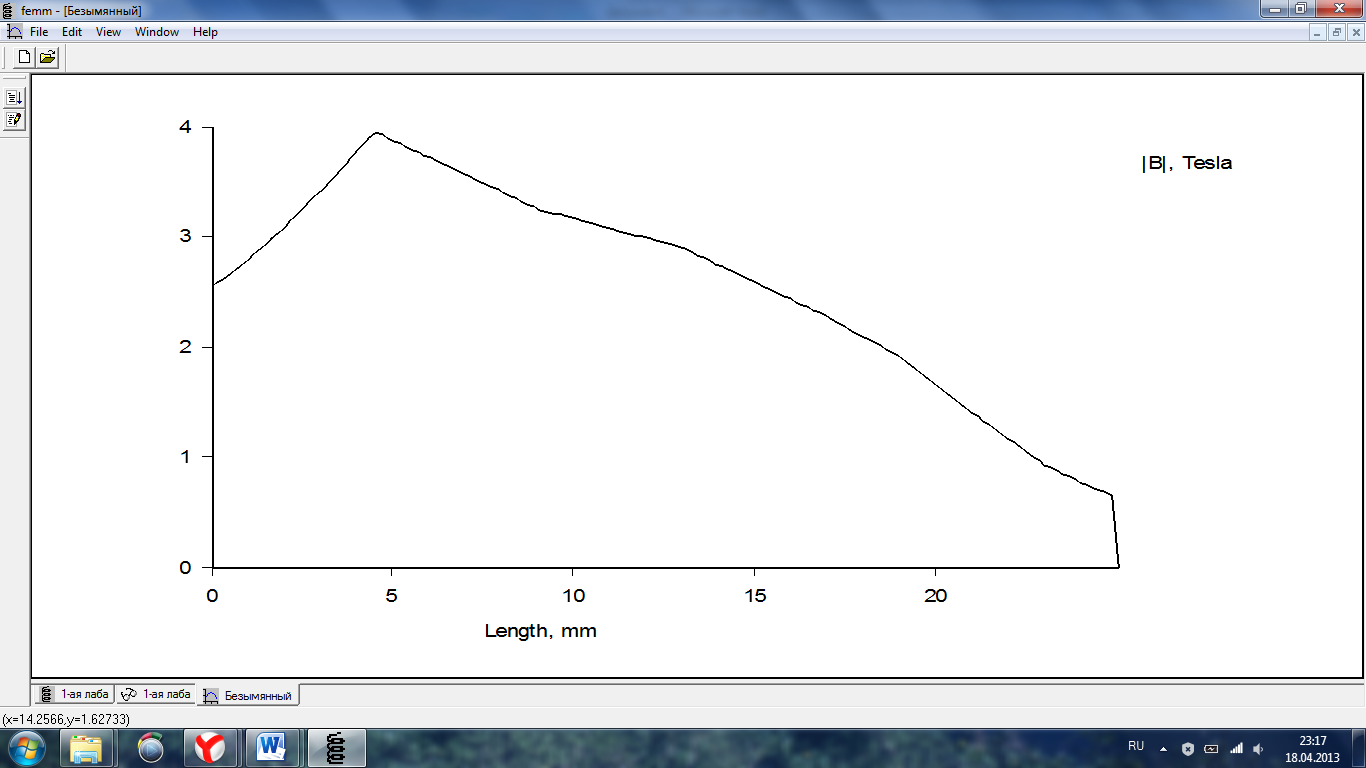
Рис.7 Кривые изменения магнитной индукции.
6. Рассчитать магнитное напряжение между полюсами (полюсом и плоскостью) по различным путям интегрирования
Список использованной литературы
1. Буль О.Б. Методы расчета магнитных систем электрических аппаратов: Магнитные цепи, поля и программа FEMM: Учеб. пособие для студентов высш. учеб. заведений/ О.Б. Буль. – М.: Издательский центр «Академия», 2005. – С. 171-257, 287-296).
