Решение.

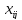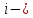Обозначим через количество единиц сырья, перевозимого изго пункта его получения на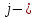е предприятие. Тогда условия доставки и вывоза необходимого и имеющегося сырья обеспечиваются за счет выполнения следующих равенств:

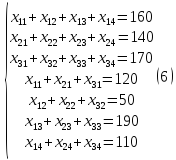
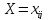
При данном плане 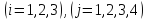перевозок общая стоимость перевозок составит

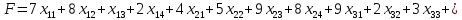
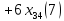
Таким образом, математическая постановка данной транспортной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений 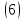, при котором целевая функция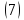принимает минимальное значение.

Глава 2. Определение опорного плана транспортной задачи.

Как при решении задачи линейного программирования симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Этот план, как уже отмечалось выше, находят методом северо-западного угла, методом минимального элемента или методом аппроксимации Фогеля. Сущность этих методов состоит в том, что опорный план находят последовательно 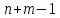шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворяющие потребности в грузе одного из пунктов назначения (того, в столбце которого находятся заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находятся заполняемая клетка).

В первом случае временно исключают из рассмотрения столбец, содержащий заполненную на данном шаге клетку, и рассматривают задачу, таблица условий которой содержит на один столбец меньше чем было перед этим шагом, но то же количество строк и соответственно измененные запасы груза в одном из пунктов отправления (в том, за счет запаса которого была удовлетворена потребность в грузе пункта назначения на данном шаге).Во втором случае временно исключает из рассмотрения строку, содержащую заполненную клетку, и считают, что таблица условий имеет на одну строку меньше при неизменном количестве столбцов и при соответствующем изменении потребности в грузе в пункте назначения, в столбце которого находятся заполняемая клетка.

После того как проделаны 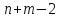описанных выше шагов, получают задачу с одним пунктов отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают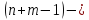й шаг и получают искомый опорный план. Следует заметить, что на некоторые шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправления. В этом случае также временно из рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равным нулю. Этот нуль записывают в очередную заполняемую клетку. 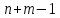Указанные выше условия гарантируют получениезанятых клеток, в которых стоят компоненты опорного плана, что является исходным условием для проверки последнего на оптимальность и нахождения оптимального плана.