
- •Курсова робота
- •§ 1. Декартова реалізація системи аксіом евклідової геометрії (за о.В. Погорєловим)
- •1.1. Несуперечливість системи аксіом евклідової геометрії
- •1.2. Повнота системи аксіом евклідової геометрії
- •1.3. Незалежність аксіоми існування відрізка заданої довжини
- •1.4. Незалежність аксіоми паралельних.
- •§ 2. Арифметична реалізація векторної системи аксіом г. Вейля евклідової геометрії
- •2.1. Несуперечливість системи аксіом г. Вейля евклідової геометрії для простору те3
- •2.2. Незалежність системи аксіом г. Вейля
- •2.3. Повнота системи аксіом Вейля
- •3.1. Реалізація Бельтрамі - Клейна
- •Реалізація Пуанкаре
- •Висновки
- •Говорячи про несуперечливість системи аксіом, то вона називається незалежною (мінімальною), якщо кожна аксіома даної системи не є логічним наслідком інших аксіом цієї системи.
- •Список використаних джерел
1.2. Повнота системи аксіом евклідової геометрії
Питання про повноту системи аксіом тісно пов'язане з питанням про ізоморфізм всіх її реалізацій.
Означення 6. Дві реалізації R і R ' деякої теорії Т називаються ізоморфними, якщо між елементами цих реалізацій (що відповідають основним поняттям теорії Т) можна встановити взаємно однозначну відповідність, яка зберігає відношення, встановлені аксіомами [14,c.94].
Теорема 1. Якщо всі реалізації системи аксіом теорії Т ізоморфні, то ця система аксіом повна.
Доведення.
Припустимо
супротивне: нехай всі реалізації системи
аксіом теорії Т
ізоморфні,
але система аксіом Т
неповна.
Це означає,
що існує деяке твердження a, яке не може
бути
виведене з аксіом Т
і не знаходиться з ними н суперечності.
Тоді можна утворити дві несуперечливі
системи аксіом
 і
і приєднуючи до аксіом Т аксіому
приєднуючи до аксіом Т аксіому або її заперечення
або її заперечення .
.
Нехай
 і
і
 - реалізації систем аксіом
- реалізації систем аксіом і
і
 .
Кожна
з них є одночасно реалізацією Т.
Оскільки в T
має місце
.
Кожна
з них є одночасно реалізацією Т.
Оскільки в T
має місце
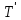 ,
має місцеa
, то ці реалізації не ізоморфні. Прийшли
до суперечності, яка й доводить теорему.
,
має місцеa
, то ці реалізації не ізоморфні. Прийшли
до суперечності, яка й доводить теорему.
Теорема 2. Система аксіом евклідової геометрії є повною, тобто не можна приєднати до неї жодних нових аксіом, які б не випливали з уже прийнятих аксіом і не суперечили їм.
Доведення. Згідно з теоремою 1 для доведення даної теореми досить установити ізоморфізм всіх реалізацій системи аксіом евклідової геометрії. Оскільки дві реалізації, ізоморфні третій, є ізоморфними між собою, то досить довести ізоморфізм всіх реалізацій декартовій реалізації. Встановимо такий ізоморфізм.
Нехай
R
- яка-небудь реалізація системи аксіом
евклідової геометрії на площині.
Побудуємо аналітичну геометрію, яка
відповідає цій реалізації. Введемо на
площині прямокутну декартову систему
координат точно так, як це робиться в
аналітичній геометрії. Тоді кожна пряма
на площині буде задаватись лінійним
рівнянням
 .
Для відстані між точками виводиться
формула
.
Для відстані між точками виводиться
формула

Поставимо
тепер у відповідність точці (х;
у)
декартової
реалізації точку реалізації R
з координатами х, у;
прямій
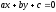 декартової
реалізації - пряму в реалізації R,
яка
задається таким самим рівнянням. Ця
взаємно однозначна відповідність між
точками і прямими декартової реалізації
і точками і прямими реалізації R
є ізоморфізмом.
декартової
реалізації - пряму в реалізації R,
яка
задається таким самим рівнянням. Ця
взаємно однозначна відповідність між
точками і прямими декартової реалізації
і точками і прямими реалізації R
є ізоморфізмом.
Дійсно,
якщо в декартовій реалізації точка
А
лежить
на прямій а
і
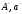 -
відповідні
точка і пряма в реалізації R,
то
-
відповідні
точка і пряма в реалізації R,
то
 лежить на прямійа'.
лежить на прямійа'.
Відповідні відрізки декартової реалізації і реалізації R мають однакові довжини, оскільки виражаються однією й тією ж формулою через координати кінців.
Отже, встановлена нами взаємно однозначна відповідність між точками і прямими декартової реалізації і довільної реалізації R -ізоморфізм. Звідси випливає, що всі реалізації системи аксіом евклідової геометрії ізоморфні і, отже, за теоремою 1 система аксіом евклідової геометрії повна [6,c.255].
1.3. Незалежність аксіоми існування відрізка заданої довжини
Щоб довести незалежність деякої аксіоми а від інших аксіом теорії T, досить побудувати таку реалізацію R системи аксіом теорії Т в якій аксіома а не виконується. Якщо таку реалізацію вдається побудувати, то аксіома а - незалежна. Дійсно, якби аксіома а була наслідком інших аксіом, то це було б і в реалізації R, тобто в R було б справедливе твердження a, що суперечить побудові R.
Цим способом ми й доведемо незалежність аксіоми існування відрізка даної довжини від інших аксіом евклідової геометрії. [3,c.420].
Теорема 3. Аксіома існування відрізка заданої довжини незалежна, тобто не може бути одержана як наслідок з інших аксіом евклідової геометрії.
Доведення. Позначимо через G сукупність дійсних чисел, яка містить всі раціональні числа, а також всі числа, які одержуються з раціональних чисел за допомогою скінченного числа дій додавання, віднімання, множення, ділення і добування квадратного кореня. Числами із G не вичерпуються всі дійсні числа.
Побудуємо
тепер декартову
реалізацію системи аксіом тим самим
способом, що й раніше, але будемо
користуватись при цьому лише числами
із G.
Наприклад,
точкою назвемо пару чисел ізG,
прямою
- сукупність точок, які задовольняють
рівняння
ізG,
прямою
- сукупність точок, які задовольняють
рівняння
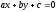 з
коефіцієнтами а,
b,
с із
G
і
т.д. Перевіряючи виконання аксіом, ми
слово в слово повторимо всі проведені
нами раніше доведення. При цьому
встановимо виконання всіх аксіом, крім
аксіоми існування відрізка даної
довжини. Ця аксіома в даній реалізації
не буде виконуватися. Дійсно, довжина
відрізка з кінцями
з
коефіцієнтами а,
b,
с із
G
і
т.д. Перевіряючи виконання аксіом, ми
слово в слово повторимо всі проведені
нами раніше доведення. При цьому
встановимо виконання всіх аксіом, крім
аксіоми існування відрізка даної
довжини. Ця аксіома в даній реалізації
не буде виконуватися. Дійсно, довжина
відрізка з кінцями
 в
даній
реалізації
визначається за формулою
в
даній
реалізації
визначається за формулою

Через
те що числа
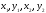
 G,
то
й d
G,
то
й d
 G.
Оскільки
ж числа G
не
вичерпують всіх дійсних чисел, то
знайдеться таке дійсне число d,
яке
в даній реалізації не може бути довжиною
жодного відрізка. Наприклад, у даній
реалізації не існує відрізка довжиною
G.
Оскільки
ж числа G
не
вичерпують всіх дійсних чисел, то
знайдеться таке дійсне число d,
яке
в даній реалізації не може бути довжиною
жодного відрізка. Наприклад, у даній
реалізації не існує відрізка довжиною
 .
.
Таким чином, аксіома існування відрізка даної довжини залежить від інших аксіом евклідової геометрії [13,c.311].
