Документ Microsoft Office Word

Геометрический и механический смысл производной

Геометрический смысл производной

Пусть функция  определена в некоторой окрестности  токи , непрерывна в этой точке и , а  (рис.2).

Рис. 2

Придав произвольное приращение аргументу , так чтобы , перейдем к точке  с абсциссой  и ординатой , где .

Уравнение прямой, проходящей через точки  и  (секущей графика функции , имеет вид: , где отношение  представляет собой угловой коэффициент секущей (.

Касательной к графику функции  в точке  называется предельное положение секущей , при стремлении точки  по графику  к точке .

Для того, чтобы секущая  при  стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел , то есть , чтобы существовала конечная производная функции  в точке .

Угловой коэффициент касательной получается путем перехода от  к пределу при :

Таким образом, получим, что , где  - угол наклона касательной к оси (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции  в точке  имеет вид

В случае бесконечной производной .

Из уравнения секущей имеем:

Переходя в равенстве к пределу при , получаем уравнение касательной к графику функции в точке  в виде , то есть касательная является в данном случае вертикальной прямой, проходящей через точку  оси абсцисс.

Механический смысл производной

Пусть материальная точка движется прямолинейно и  - длина пути, проходимого за время , отсчитываемого от некоторого момента времени .

Для определения скорости  в данный момент  придадим переменной некоторое приращение , при этом приращение пути будет равно .

Отношение  называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени , и обозначается

Предел  называется величиной мгновенной скорости движения в момент времени .

Таким образом, мгновенная скорость в момент времени  прямолинейного движения, совершаемого по закону  равна значению производной .

Примеры задач

Задача 1. Составьте уравнение общей касательной к графикам функций  и .

Решение.

I способ.

Прямая  является общей касательной графиков функций  и , если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.

- уравнение касательной к графику функции y=x² в точке с абсциссой x₀

- уравнение касательной к графику функции y=x³ в точке с абсциссой x₁

Прямые совпадают, если их угловые коэффициенты и свободные члены равны. Отсюда

Решением системы будут

Уравнения общих касательных имеют вид:

II способ.

Уравнение касательной к кривой  в точке с абсциссой  имеет вид:

Для касания прямой  параболы  достаточно, чтобы дискриминант квадратного уравнения  был равен нулю.

Заметим, что: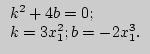 

Получаем 

Ответ: Уравнения общих касательных имеют вид:  и .

Задача 2. График функции  пересекает ось абсцисс в точке , а касательная к графику пересекает ось абсцисс в точке . Напишите уравнение этой касательной, если точка  делит пополам отрезок , где  - начало координат.

Решение.

Найдем абсциссу точки , решив уравнение .

Точка  имеет координаты . - середина отрезка , значит, точка  имеет координаты .

Функция  определена при  и дифференцируема при .

Составим уравнение касательной в точке графика с абсциссой .

Касательная проходит через точку . Значит,

Решим это уравнение.

Уравнение касательной имеет вид:

Ответ: .

Задача 3. Точка движется прямолинейно под действием постоянной силы с ускорением 2 м / с и с нулевой начальной скоростью. Через три секунды после начала движения сила прекращает действовать, и точка начинает двигаться равномерно с набранной скоростью. Найдите закон движения точки.

Решение. Выберем систему координат так, чтобы в начальный момент времени точка находилась в начале координат, то есть при .

Закон движения  при  имеет вид: при . При  графиком движения является прямая - касательная к параболе , проведенная в точке . Найдем уравнение этой касательной.

Таким образом, закон движения имеет вид: 

Ответ: 

Задача 4. Паром подтягивается к берегу при помощи каната, который наматывается на ворот со скоростью 40 м / мин. Ворот находится на берегу на 10 м выше поверхности воды. Найдите:

а) скорость движения парома в тот момент, когда он находится в 30 м от берега;

b) скорость движения парома в тот момент, когда длина натянутого каната равна 50 м.

Решение.

а) Пусть  м - расстояние от парома до берега. В выбранной системе координат в точке  находится ворот, паром - в точке (рис. 3).

По теореме Пифагора:

 

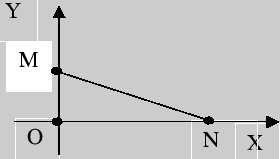
Рис. 3

При наматывании каната на ворот расстояние 

уменьшается. Значит, 

С другой стороны, 

При  получаем

Из решения уравнения  находим искомую скорость движения: (м / мин). Знак ``минус'' означает, что паром приближается к берегу.

b) , .

Получаем: . Откуда .

Ответ:

Задачи для самостоятельного решения

1. Составьте уравнение всех касательных к графику функции , которая проходит через точку A:

Сколько существует решений в зависимости от выбора точки?

2. На графике функции  найдите все точки, касательная в каждой из которых к этому графику отсекает от отрицательной полуоси ОХ отрезок вдвое меньше, чем от положительной полуоси ОУ.

3. На графике функции  найти все такие точки, касательная в каждой из которых к графику пересекает положительные полуоси и отсекает от них равные по длине отрезки.

4. Доказать, что касательная к гиперболе  образует с осями координат треугольник постоянной площади, а точка касания является центром окружности, описанной около этого треугольника.

5. График функции  пересекает ось абсцисс в точке К, а касательная к графику пересекает ось абсцисс в точке С. Напишите уравнение этой касательной, если начало координат является серединой отрезка КС.

6. Напишите уравнение касательной к графику функции , не пересекающей прямой .

7. Прямая  является касательной к графику функции . Найдите координаты точки касания.