33 группа / 4. Непрерывность. Производная

Занятие № 4. Непрерывность функции. Техника вычисления производных

Вопросы:

1. Непрерывная в точке функция.

2. Непрерывность сложной функции.

3. Точка разрыва.

4. Классификация точек разрыва.

5. Определение производной.

6. Таблица производных. Правила дифференцирования.

Принести таблицу производных

Домашнее задание

4.1. Исследовать функции на непрерывность. В случае разрыва указать его род.

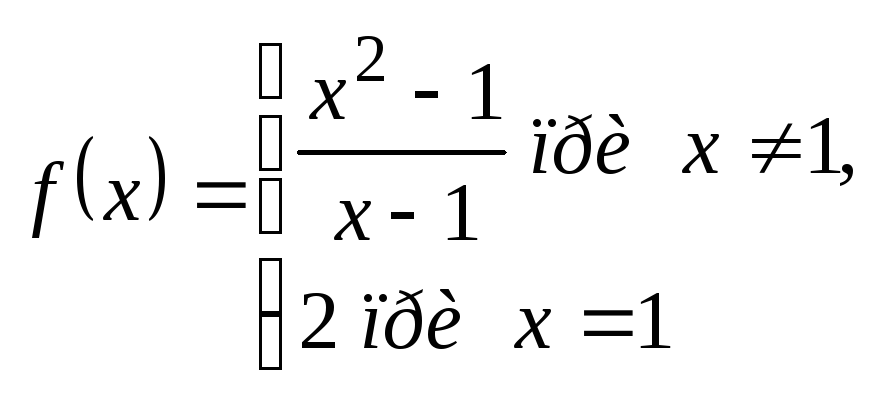а) ; б) ; в).

4.2. Найти по определению производную функции .

4.3. Найти производные функций: а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) ; и) .

Аудиторные задания

4.1. Исследовать на непрерывность в точке функцию:

а); б).

2. Исследовать функции на непрерывность. Построить графики.

а)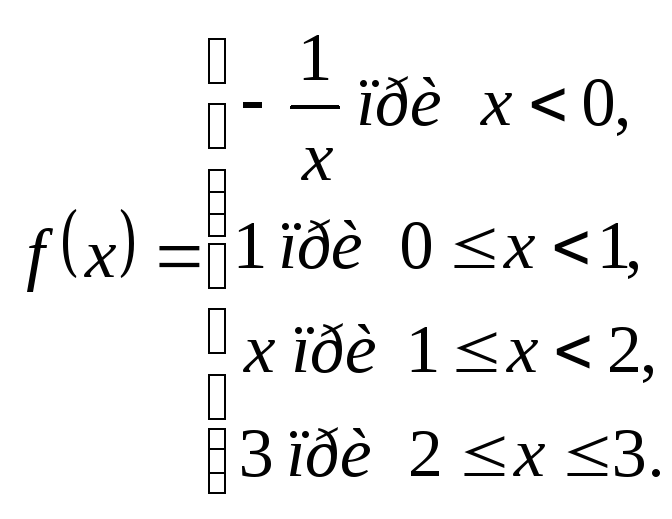; б)

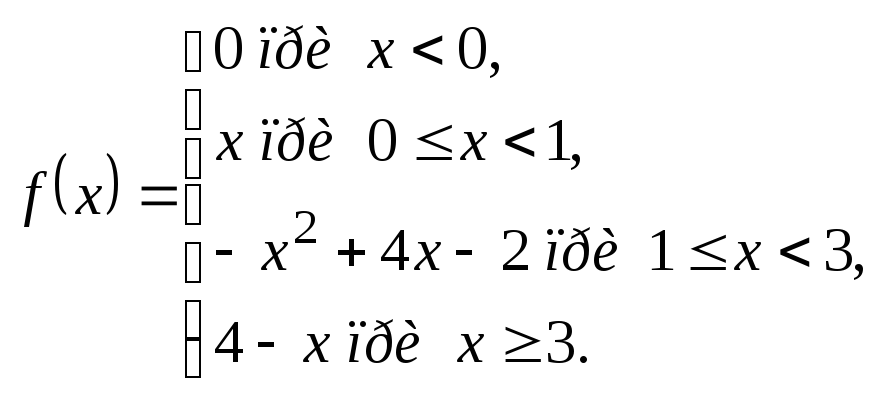
4.3. Найти по определению производную функции а); б) .

4.4. Найти производную в точке .

4.5. Найти производные функций: а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) ; и) ; к) ; л) ; м) ; н) ; о) ; п) .