
Уравнение Лапласа.
Многие стационарные
задачи (течение несжимаемой жидкости,
задачи теплопроводности и диффузии в
стационарных случаях, форма нагруженной
мембраны) сводятся к решению уравнения
Пуассона:
 ,
то получаем уравнение Лапласа:
,
то получаем уравнение Лапласа:
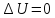 .
.
Для простоты рассмотрим двумерное уравнение Лапласа:
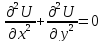
Пусть
 область изменения
область изменения
 - ограничена замкнутой линией
- ограничена замкнутой линией
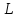 .
Граничное условие на границе
.
Граничное условие на границе
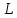 зададим в виде:
зададим в виде:
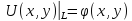 .
.
Задача, состоящая в решении уравнения Лапласа (или Пуассона) при заданных значениях искомой функции на границе расчетной области – называется задачей Дирихле.
Для простоты примем
заданную область
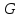 в виде прямоугольника.
в виде прямоугольника.
|
|
Нанесем
сетку с одинаковым шагом
Эту схему можно записать в виде:
|
|
|
|
Значения сеточной функции в узлах на границе могут быть найдены из граничного условия:
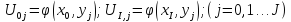
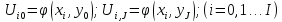
В теории разностных схем доказывается, что решение построенной разностной задачи существует, а сама схема устойчива.
Одним наиболее распространенным методом решения такой системы является итерационный метод.
Каждое из уравнений
запишем в виде, разрешенным относительно
значения
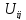 в центральном узле.
в центральном узле.
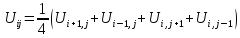
В представленном
алгоритме предусмотрено задание
начальных значений
 .
Иногда полагают
.
Иногда полагают
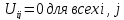 .
Итерации заканчиваются, когда значения
сеточной функции в узлах на последовательных
итерациях отличаются на заданную
величину
.
Итерации заканчиваются, когда значения
сеточной функции в узлах на последовательных
итерациях отличаются на заданную
величину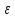 .
.
Аппроксимация
начального условия в виде:
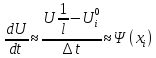 ухудшает аппроксимацию, так как она
имеет первый порядок погрешности. И
общая погрешность становится
ухудшает аппроксимацию, так как она
имеет первый порядок погрешности. И
общая погрешность становится
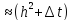 .
Положение можно исправить, если задать
более точную аппроксимацию, чем:
.
Положение можно исправить, если задать
более точную аппроксимацию, чем:
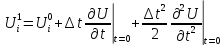
Вместо
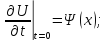 а вместо
а вместо
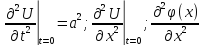
то есть, используем основное уравнение, тогда:
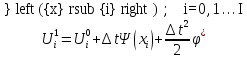
Метод Хокии численного решения уравнения Пуассона
В общем случае решение эллиптических уравнений, к которым относится уравнение Пуассона, представляет значительные трудности и требует длительного времени.

Однако, свойство симметрии уравнения Пуассона, которое является следствием оператора Лапласа, позволяет свести решение многомерного уравнения к раздельному решению одномерных задач. Метод Хокии в своей простейшей форме применяет преобразование Фурье на одной пространственной координате, в результате относительной другой координаты остаются несвязанные трехдиагональные матричные условия, которые легко решить, в частности методом прогонки (или циклической редукции).
Итак, рассмотрим
уравнение Пуассона:
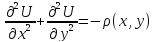 ,
которое нужно решить для прямоугольной
области D,
на которую наложена сетка с шагом
,
которое нужно решить для прямоугольной
области D,
на которую наложена сетка с шагом
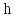 .
.
|
|
1)
Если периодические условия, то и по
2)
Если на границах нулевые значения
В качестве примера выберем граничные условия, задающие постоянный потенциал на концах каждого столбца:
С
Считается, что
в некоторых узлах в некотором множестве
узлов, известны значения
|
А можно брать в
узлах именно те значения, которые
непрерывная функция
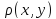 принимает в узлах
принимает в узлах
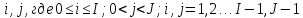 .
.
При этом надо иметь ввиду, что:
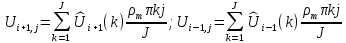
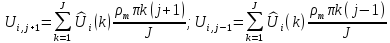
Подставив это в разностное уравнение, получим:
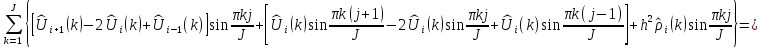
Рассмотрим два члена, их можно представить так:
И тогда наше уравнение имеет вид:
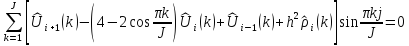
Чтобы равенство
выполнялось при любых
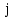 ,
то есть, в каждой точке
,
то есть, в каждой точке
 в этих уравнениях можно приравнять к
нулю отдельно амплитуду каждой
____________ __________.
в этих уравнениях можно приравнять к
нулю отдельно амплитуду каждой
____________ __________.
Мы должны приравнять к нулю, что дает:
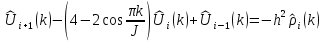
Таким образом, для
каждого
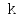 мы получим трехдиагональное матричное
уравнение.
мы получим трехдиагональное матричное
уравнение.
При этом
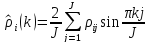 .
.
Иными словами мы
получили для каждого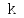 одномерное уравнение, которое можно
решить методом прогонки.
одномерное уравнение, которое можно
решить методом прогонки.
После решения всех
трехдиагональных уравнений мы получим
значения
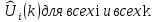 .
Потенциал в каждой узловой точке
определяется суммой ряда Фурье:
.
Потенциал в каждой узловой точке
определяется суммой ряда Фурье:
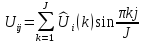
Этот метод
заключается в разложении Фурье по одной
из независимых переменных (у нас по
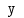 )
и последующей
прогонке по другой переменной
)
и последующей
прогонке по другой переменной
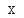 и требует выполнения примерно
и требует выполнения примерно
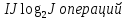 - является быстродействующим.____________________
- является быстродействующим.____________________

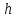 по
по
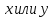 .
Значения
.
Значения
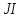 в
узлах
в
узлах
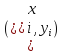 значениями сеточной функции
значениями сеточной функции
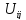 .
Тогда используя конечно-разностную
аппроксимацию и используя пятиточечный
шаблон
.
Тогда используя конечно-разностную
аппроксимацию и используя пятиточечный
шаблон
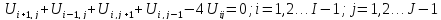
 или постоянные значения, то разложение
по
или постоянные значения, то разложение
по
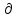 опустим:
опустим:
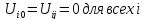
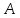 как с граничными условиями на краях
– тоже нулевые граничные условия и
тогда ис______ разложение по
как с граничными условиями на краях
– тоже нулевые граничные условия и
тогда ис______ разложение по
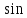 .
.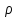 .
То есть, если
.
То есть, если
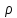 было разбито непрерывно по узлам, мы
собираем узлы (так делают, например,
в задачах, где
было разбито непрерывно по узлам, мы
собираем узлы (так делают, например,
в задачах, где
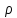 - это некоторый заряд в пространстве).
- это некоторый заряд в пространстве).