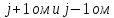Решение дифференциальных уравнений в частных производных второго порядка методом конечных разностей (решение основных краевых задач математической физики).
Многие научные и технические задачи приводят к необходимости решения так называемых уравнений математической физики. Основные из них следующие:
1) Волновое
уравнение
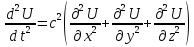
Описывает поведение
различных видов волн упругих, звуковых,
электромагнитных и т.д. в различных
средах,
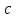 - скорость распространения волны в
данной среде.
- скорость распространения волны в
данной среде.
2) Уравнение
диффузии
(или теплопроводности)
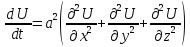
Описывает процесс распространения тепла в однородном изотропном теле.
3) Уравнение
Пуассона
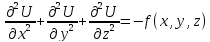
Описывает установившиеся статические (электрические __ магнитные, тепловые) потенциалы механические напряжение в конструкциях.
Если
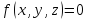 ,
то мы получаем
,
то мы получаем
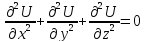
Описывает, в частности, потенциалы поля тяготения, электрического поля – в отсутствии масс и электрических зарядов.
Если к каждому из этих уравнений добавить дополнительные граничные и начальные условия, то мы получим ______ краевые задачи математической физики.
Основные моменты:
1) В разностных уравнениях в левой части
всегда только
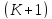 или
или 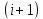
2) Явная схема решается рекуррентно, неявная – проточкой
3) для
разностного уравнения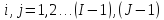
для гр. условий
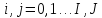
для волнового
уравнения:
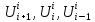 – явная,
– явная,
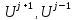 – неявная.
– неявная.
для теплопровода:
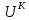 - явная,
- явная,
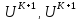 - неявная.
- неявная.
Численные методы решения уравнений в частных производных (УЧП).
Описывают широкий круг физических задач в областях механика, электродинамика, теория упругости, термодинамика и многих других. Аналитические решения удаются в простых задачах.
Основные методы численного решения: метод сеток, метод прямых, метод характеристик, метод установления и другие. Наиболее развитый и употребительный – метод сеток.
Уравнения в частных производных – основные уравнения математической физики. Делятся на: гиперболические, параболические и эллиптические.
Основные определения
в общем виде:
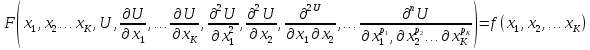
Здесь

Наивысший порядок
в данном уравнении производной называется
порядком дифференциального уравнения.
Если
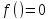 ,
то уравнение называется однородным,
если
,
то уравнение называется однородным,
если
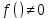 ,
то неоднородным.
,
то неоднородным.
Для выделения
единственного решения необходимо
задавать дополнительные условия, в
которые будут входить функции с числом
аргументов
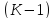 .
.
К ним относятся:
- задание значений
искомой функции на поверхности размерности
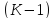 в пр-ве неизменных
в пр-ве неизменных
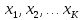 .
.
Рассмотрим уравнения
классической физики. В них независимые
переменные (время
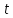 ,
пространственные координаты: декартовы,
цилиндрические, серерические).
,
пространственные координаты: декартовы,
цилиндрические, серерические).
Если время
присутствуют, то задача называется
нестационарной или эволюционной. Если
времени
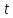 нет, то стационарной задачей с одной
переменной – одномерная соответствует
двумерной, трехмерной.
нет, то стационарной задачей с одной
переменной – одномерная соответствует
двумерной, трехмерной.
Классическое уравнение гиперболического типа – волновое.
Классическое уравнение параболического типа – теплопроводности.
Классическое уравнение эллиптического тип – Лапласа, Пуассона.
Задача Коши – задача с начальными условиями.
Краевые или граничные задачи.
Смешанные краевые задачи – краевые задачи с начальными условиями.
Метод конечных разностей (метод сеток) – основной метод решения дифференциальных уравнений в частных производных.
Суть метода заключается в том, что решение дифференциального уравнения сводится к решению систем алгебраических уравнений с достаточно разреженными матрицами.
Основные этапы метода мы указали при решении ОДУ.
Основные понятия и этапы применимо к ЧДУ. Продемонстрируем на примере решения задачи Дирихле для классического уравнения эллиптического типа – уравнения Лапласа.
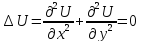
Граничное условие:
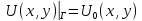
На первом этапе
область
 непрерывного изменения аргумента с
границей
непрерывного изменения аргумента с
границей
 заменяют приближающей и сеточной
областью
заменяют приближающей и сеточной
областью
 с границей
с границей
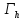 .
Для этого проверяем линии
.
Для этого проверяем линии
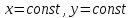 с
шагом
с
шагом
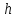 .
Точки пересечения назовем узлы.
.
Точки пересечения назовем узлы.
|
|
Узлы
внутренние – если четыре соседних
узла принадлежат
Узлы
граничные – если не принадлежат
На втором этапе заменяем дифференциальный оператор разностным оператором:
|
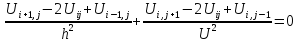
записав его для всех внутренних точек, получаем:
Аппроксимация граничных условий.
Для области
произвольной формы значения сеточной
функции в граничных узлах принимаются
равными значениям функции
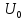 в ближайших (по заданному критерию)
точках кривой
в ближайших (по заданному критерию)
точках кривой
 .
Число уравнений системы (в данном случае
____ уравнений) равно числу внутренних
узлов разности сетки.
.
Число уравнений системы (в данном случае
____ уравнений) равно числу внутренних
узлов разности сетки.
Принимаем сетку уравнений в виде:
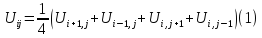
Видно, что значение функции в центральной точке есть среднее арифметическое значение функции в четырех средних точках.
Отметим, что каждое
уравнение содержит лишь пять неизвестных,
хотя вся система содержит
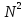 – неизвестных, то есть, сколько внутренних
узлов. Таким образом, система является
сильно разряженной.
– неизвестных, то есть, сколько внутренних
узлов. Таким образом, система является
сильно разряженной.
Она может быть решена различными методами:
Метод простой итерации. Для простоты предположим, что область прямоугольник.
|
|
Зададим
начальное приближенное значение
искомой функции во внутренних узлах.
Например, значение функции можно
принять как результат интерполяции
на область
|
Возьмем узел (1):
Примем
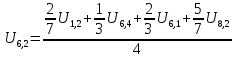
Узел
1 отделен от узла
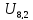 на два шага, а от узла
на два шага, а от узла
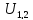 на пять шагов, следовательно, можно
поставить коэффициенты
на пять шагов, следовательно, можно
поставить коэффициенты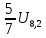 ,
,
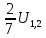 .
Ближний угол обладает большим влиянием.
Так можно определить начальное приближение
во всех внутренних узлах. Затем по
формуле (1) определить второе приближенное
во всех внутренних узлах и т.д. Доказывается,
что при любом начальном приближении
итерационный процесс сходится. Число
итерации
.
Ближний угол обладает большим влиянием.
Так можно определить начальное приближение
во всех внутренних узлах. Затем по
формуле (1) определить второе приближенное
во всех внутренних узлах и т.д. Доказывается,
что при любом начальном приближении
итерационный процесс сходится. Число
итерации
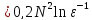
Метод статистических испытаний (метод блуждающей точки).
В этом методе последовательно определяется значения функций в каждом внутреннем узле. Суть метода заключается в следующем: Берется произвольный внутренний узел, запускается генератор СВ – например, имеющий равномерное распределение в интервале 0-1. И принимается, например такое правило: 0-0,2 – блуждающая точка сдвигается из исходного узла на шаг вправо (то есть на соседний узел вправо), 0,2-0,4 – влево; 0,4-0,6 – вверх; 0,6-0,8 – вниз; 0,8-1,0 – остается на месте. Генератор включается на каждом шаге до тех пор, пока блуждающая точка не окажется в граничном узле.
Если многократно промоделировать движение точки из исходного внутреннего узла и при каждом испытании фиксировать граничную точку, в которую попадает блуждающая точка, то значение функции в исходном узле можно считать равным оценке математического ожидания, вычисляемого по соотношению:
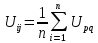
где
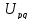 - граничное значение
- граничное значение
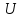 .
.
Метод очень эффективен по памяти, так как не нужно помнить информацию об о_______ внутренних узлах.
Метод прямых. Суть метода заключается в замене решения ДУЧП ______ обыкновенных дифференциальных уравнений. Уравнения ЧП рассматривается на линиях параллельных одной из координатных осей. Это приводит к исчезновению зависимости от одной из независимых переменных.
|
|
|
С шагом
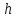 проведем параллельные прямые через
точку
проведем параллельные прямые через
точку
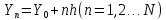 .
Предположив достаточную _________ функции
.
Предположив достаточную _________ функции
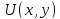 ,
подставим в уравнение
,
подставим в уравнение
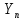 и заменим производную по
и заменим производную по
 разностной аппроксимацией, то получим
разностной аппроксимацией, то получим
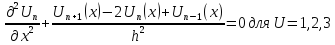 .
.
То есть, мы получим
систему обыкновенных дифференциальных
уравнений (зависящих только от
 ).
).
Граничные условия:
|
|
|
Это система обыкновенных дифференциальных уравнений может решаться численно или аналитически.
Этот метод можно
рассматривать как продленный случай
метода сеток, когда
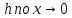 .
.
Существенная
особенность: если
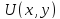 меняется изначально, то можно сделать
только две или ___ полосы, что существенно
упрощает задачу.
меняется изначально, то можно сделать
только две или ___ полосы, что существенно
упрощает задачу.
Рассмотрим краевую задачу, связанную с волновым уравнением.
Для простоты
рассмотрим одно____ случай, тогда
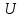 зависит только от одной простр__ой
координаты
зависит только от одной простр__ой
координаты
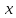 .
Физически это соответствует поперечным
колебаниям тонкого стержня или прод__ным
колебаниям стержня, когда его _____
совершают плоскопараллельные колебательные
движения.
.
Физически это соответствует поперечным
колебаниям тонкого стержня или прод__ным
колебаниям стержня, когда его _____
совершают плоскопараллельные колебательные
движения.
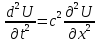
Искомая функция
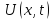 ________ положение струны в момент
________ положение струны в момент
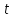 ,
то есть ее отклонение от положения
равновесия. Простейшей задачей для
этого уравнения является задачи Коши,
то есть задаются начальные условия
(два, так как количество условий равно
порядку производной). То есть описывается
начальная форма струны и скорость ее
точек
,
то есть ее отклонение от положения
равновесия. Простейшей задачей для
этого уравнения является задачи Коши,
то есть задаются начальные условия
(два, так как количество условий равно
порядку производной). То есть описывается
начальная форма струны и скорость ее
точек
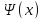 в начальный момент.
в начальный момент.
Начальное условие:
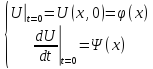
На практике чаще
решается не задача Коши для бесконечной
струны, а смешанная задача для ограниченной
струны
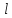 .
В этом случае задают граничные условия
на концах струны.
.
В этом случае задают граничные условия
на концах струны.
В частности, если
концы струны закреплены, то граничные
условия имеют вид:
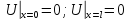
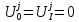
Рассмотрим некоторые
разностные схемы для этой задачи. Уже
две независимые переменные
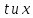 введем сетку, то есть разобьем ось
введем сетку, то есть разобьем ось
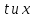 на струны соответственно с шагами
на струны соответственно с шагами
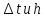 .
.
Каждому узлу сетки
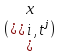 будет соответствовать значение сеточной
функции
будет соответствовать значение сеточной
функции
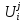 .
Заменим производные их конечноразностной
аппроксимацией следующим образом:
.
Заменим производные их конечноразностной
аппроксимацией следующим образом:
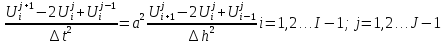
Здесь производная
по пространству записана для момента
времени
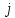 ,
а производится по времени для точки
пространства
,
а производится по времени для точки
пространства
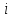 и тоже момента времени
и тоже момента времени
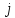 .
Отметим, что совокупность узлов при
фиксированном времени
.
Отметим, что совокупность узлов при
фиксированном времени
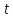 называется слоем, то есть справа за___
для слоя
называется слоем, то есть справа за___
для слоя
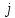 .
.
|
|
|
|
Отсюда можно найти
явное выражение для изменения сеточной
функции на
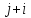 слое:
слое:
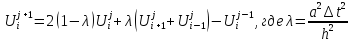
Но как видно отсюда
для этого нужно знать решения на двух
предыдущих слоях. Поэтому начать отчет
можно только с
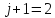 ,
а значения
,
а значения
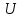 соответствующие
соответствующие
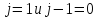 ,
то есть соответствующие нулевому и
первому слою найти из начальных условий.
,
то есть соответствующие нулевому и
первому слою найти из начальных условий.
Делается это так:
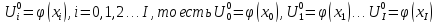
Для получения
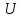 на первом слое воспользуемся вторым
начальным условием:
на первом слое воспользуемся вторым
начальным условием:
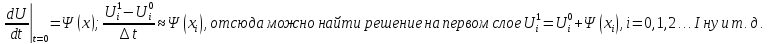
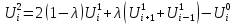
Естественно при
этом при учете граничных условий, надо
учитывать, что
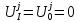 ,
значения
,
значения
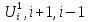 - естественно находятся из
- естественно находятся из
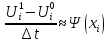 .
.
__________ ___________ схема
имеет второй порядок аппроксимации
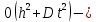 погрешность
решения, с учетом заданных граничных и
начальных условий.
погрешность
решения, с учетом заданных граничных и
начальных условий.
Эта схема условно
устойчива. Необходимое и достаточное
условие устойчивости имеет вид
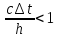 .
Таким образом, схема сходится к исходной
задаче со скоростью
.
Таким образом, схема сходится к исходной
задаче со скоростью
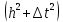 .
Здесь на слое
.
Здесь на слое
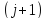 неизвестная функция
неизвестная функция
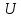 только в узле
только в узле
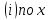 .
.
Существуют и
другие схемы.
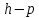 неявная. Это схемы обычно абсолютно
устойчивы, то есть снимаются ограничения
на величину шага, но при этом алгоритм
естественно усложняется:
неявная. Это схемы обычно абсолютно
устойчивы, то есть снимаются ограничения
на величину шага, но при этом алгоритм
естественно усложняется:
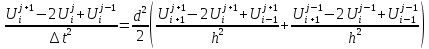
|
|
Производная по времени аппроксимируется трех точками _______. Производная
по
слоях.
|
Отсюда:
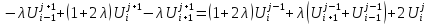
Полученная схема устойчива. _____ минимальных алгебраических уравнений, можно в частности решать методом прогонки.
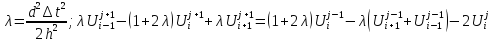
Скорость сходимости
при численных расчетах важно знать во
сколько раз ______ начальная погрешность
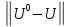 после заданного числа
после заданного числа
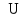 итераций:
итераций:
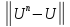 .
То есть, если
.
То есть, если
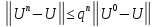 где
где
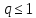 ,
то говорят, что метод сходится со
скоростью геометрической прогрессии
__________
,
то говорят, что метод сходится со
скоростью геометрической прогрессии
__________

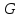
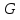 ,
хотя бы один узел.
,
хотя бы один узел.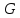 значений функции в граничных узлах.
значений функции в граничных узлах.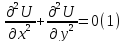
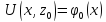
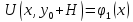
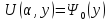
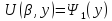
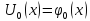
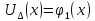
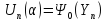
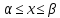
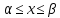
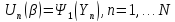
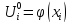
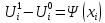
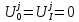
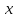 заменяется полу суммой аппроксимации
на
заменяется полу суммой аппроксимации
на