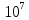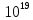Набор лекций по Выч. математике ч 1
.docxСистемы линейных уравнений.
К решению системы линейных уравнений сводятся многочисленные практические задачи, поэтому решение линейных систем – одна из самых распространенных и важных задач вычислительной математики.
Система «n» уравнений(линейных алгебраических) с «n» неизвестными имеет вид:
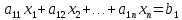
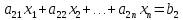
…………………………………..
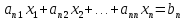
Совокупность коэффициентов этой системы можно записать в виде квадратной матрицы порядка «n»
A=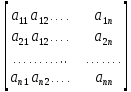
Если матрица содержит m-строк и n-столбцов, то она называется прямоугольной матрицей.
Систему (1) можно записать в матричной форме:
AX=B
Где
X=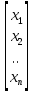 – вектор – столбец неизвестных, B=
– вектор – столбец неизвестных, B=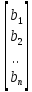 - вектор – столбец правых частей.
- вектор – столбец правых частей.
В ряде случаев получаются системы уравнений с некоторыми специальными видами матриц. Некоторые примеры:
A
=
 – симметрическая матрица (элементы
симметричны относительно главной
диагонали).
– симметрическая матрица (элементы
симметричны относительно главной
диагонали).
В
=
 - верхняя треугольная матрица (с нулевыми
элементами ниже диагонали).
- верхняя треугольная матрица (с нулевыми
элементами ниже диагонали).
С
=
 – клеточная матрица (ненулевые элементы
составляют отдельные группы (клетки)).
– клеточная матрица (ненулевые элементы
составляют отдельные группы (клетки)).
D
=
 – ленточная матрица (ненулевые элементы
составляют «ленту» параллельно
диагонали). В данном случае трех -
диагональная матрица.
– ленточная матрица (ненулевые элементы
составляют «ленту» параллельно
диагонали). В данном случае трех -
диагональная матрица.
E
=
 – единичная матрица.
– единичная матрица.
F
=
 – нулевая матрица (все элементы - нули).
– нулевая матрица (все элементы - нули).
Определителем(детерминантом) матрицы А n-го порядка называется число D(det A), равное
D
=
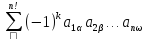 , где
, где
индексы α, β … ω – приобретают все возможные n! Перестановок номеров 1, 2….n; k – число инверсий в данной перестановке, то есть число случаев когда меньший номер идет после большего.
Необходимым и достаточным условием существования единственного решения систем линейных уравнений является условие D не равен 0. Если D = 0, то матрица называется вырожденной. В этом случае система либо не имеет решения, либо имеет бесконечное множество решений.
Эти случаи легко показать геометрически для системы

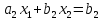
Каждому уравнению соответствует прямая. Координаты точек пересечения – есть решение системы.
Рассмотрим три возможных случая взаимного расположения прямых на плоскости:
1)Прямые
пересекаются – это значит коэффициенты
системы не пропорциональны
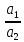 ≠
≠
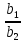 и определитель D
=
и определитель D
=
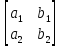 ≠ 0 – система имеет единственное решение;
≠ 0 – система имеет единственное решение;
2)Прямые параллельны – коэффициенты системы подчиняются условиям
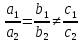
D = 0 – решение отсутствует;
3)Прямые
совпадают (все коэффициенты пропорциональны):
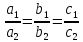
D = 0 – бесчисленное множество решений.
На практике, особенно при вычислении на ЭВМ(когда происходит округление, или отбрасывание младших результатов) определитель может быть не равен нулю: D
При D ~ 0 прямые могут оказаться почти параллельными. Координаты точки пересечения этих прямых очень чувствительны к изменению коэффициентов системы. Поэтому малые погрешности вычислений или исходных данных могут привести к существенным погрешностям в решении. Такие системы уравнений называются плохо обусловленными.
Условие D~ 0- это необходимое условие плохой обусловленности, но не достаточное.
Пример:
система уравнений n-го
порядка с диагональной матрицей(так
как только по диагонали ненулевые
элементы) с элементами
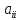 =0.1 – не является плохо обусловленной,
хотя ее определитель (D
=
=0.1 – не является плохо обусловленной,
хотя ее определитель (D
=
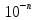 )
и близок к нулю.
)
и близок к нулю.
Методы решения линейных систем
Они делятся на две группы: прямые и итерационные.
Прямые методы используют конкретные соотношения (формулы) для вычисления неизвестных. Они просты и универсальны – пригодны для решения широкого класса линейных систем.
Однако имеют недостатки: 1)Требуют хранения в оперативной памяти сразу всей матрицы, что при больших «n» требует много памяти; 2)Они не учитывают, что могут быть разреженные матрицы с большим числом нулевых элементов, которые тоже занимают место в памяти ; 3)Накапливание погрешностей в процессе решения, поскольку на любом этапе вычисления используется результат предыдущих операций. Это очень опасно при большом «n» - то есть возрастет число операций, а также для плохо обусловленных систем, весьма чувствительных к погрешностям. Поэтому прямые методы использования при n<200 для систем с плотно заполненной матрицей и не близким к нулю определителем.
Иногда прямые методы называют точными, поскольку решения выражаются в виде точных формул. Однако точное решение может быть получено лишь при вычислениях с большим, а вернее с бесконечным числом разрядов. Однако разрядность всегда ограничена, поэтому неизбежны погрешности.
Итерационные методы – методы последовательных приближений. В начале задается некоторое приближенное решение – так называемое начальное приближение. После этого с помощью некоторого алгоритма находят новое приближение.
Проводиться один цикл вычислений, называемый итерацией. И так неоднократно – до получения решения с заданной точностью. Алгоритм итераций обычно более сложен чем в обычных методах. Объем вычислений заранее предвидеть трудно.
Итерационные модели в ряде случаев предпочтительнее. Они требуют хранения в памяти не всей матрицы, а лишь нескольких векторов с «n» компонентами, найденные элементы матрицы можно совсем не хранить, а вычислять их по мере необходимости. Погрешность здесь не накапливается поскольку определяется лишь предыдущей итерацией и, практически не зависит от ранее выполненных вычислений. Сходимость может быть медленной – поэтому ищутся эффективные пути ускорения.
Итерационные методы – могут использоваться для уточнения решений, полученных прямыми методами – то есть получаются смешанные методы, которые довольно эффективны особенно для плохо обусловленных систем.
Прямые методы
Правило Крамера – неизвестные представляется в виде отношения определителей.
Пример:

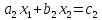
Тогда
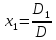 и
и
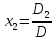 ,
где D
=
,
где D
=
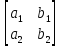 ;
;
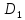 =
=
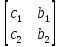 ;
;
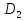 =
=
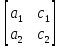
При большом числе уравнений нужно выполнить огромное количество операций.
N = (n+1)(n*n! – 1) +n,
Где (n+1)-количество определителей, (n*n!-1)-вычисление определителя, n-вычисление переменных.
Поэтому правило Крамера можно использовать для решения систем, состоящих всего из нескольких уравнений.
N~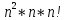 -
-
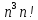
Метод
обратной матрицы
– система записывается в виде AX=B.
Умножаем обе части на обратную матрицу
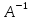 ;
X=
;
X=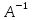 B.
Однако, если не использовать специальные
методы для вычисления обратной матрицы,
то этот метод при больших «n»
также практически не пригоден.
B.
Однако, если не использовать специальные
методы для вычисления обратной матрицы,
то этот метод при больших «n»
также практически не пригоден.
Метод Гаусса(метод исключения) – наиболее распространенный метод. Мы рассмотрим применение этого метода для решения системы лин. уравнений, вычисления определителя, вычисления обратной матрицы.
Метод
основан на приведении матрицы системы
к треугольному виду. Основная
идея алгоритма
заключается в том, что на первом этапе
с помощью первого уравнения исключается
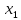 из всех последующих уравнений, на втором
этапе с помощью второго уравнения
исключается переменная
из всех последующих уравнений, на втором
этапе с помощью второго уравнения
исключается переменная
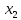 ,
из всех последующих и так далее – до
тех пор пока в левой части последнего
уравнения не останется лишь один член
с последним неизвестным
,
из всех последующих и так далее – до
тех пор пока в левой части последнего
уравнения не останется лишь один член
с последним неизвестным
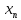 .
– эти этапы реализуют прямой
ход метода
Гаусса.
.
– эти этапы реализуют прямой
ход метода
Гаусса.
Обратный ход
– заключается в последовательном
определении
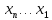 , начиная с
, начиная с
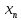 .
В последнем случае могут использоваться
методы регуляризации.
.
В последнем случае могут использоваться
методы регуляризации.
Другие задачи линейной алгебры – вычисление определителя, обратной матрицы, собственных значений матрицы и др.
Легко вычисляются лишь определители невысоких порядков и некоторые специальные типы определителей.
Определитель треугольной матрицы равен произведению элементов главной диагонали.
Определитель единичной матрицы Е равен 1.
Определитель нулевой матрицы равен 0.
Определитель
D
порядка «n»
имеет вид: D
=
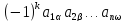 .
Из этого выражения следует, что
определитель равен сумме n!
слагаемых, каждое из которых имеет «n»
элементов. Поэтому для вычисления
определителя порядка «n»
(без использования специальных приемов)
требуется (n-1)n!
– умножений и (n!-1)
– сложений, то есть общее число
арифметических операций равно:
.
Из этого выражения следует, что
определитель равен сумме n!
слагаемых, каждое из которых имеет «n»
элементов. Поэтому для вычисления
определителя порядка «n»
(без использования специальных приемов)
требуется (n-1)n!
– умножений и (n!-1)
– сложений, то есть общее число
арифметических операций равно:
N = (n-1)n! + n!-1 = n!*n - 1~n!*n
Оценим значения N в зависимости от «n»
|
n |
3 |
10 |
20 |
|
N |
17 |
3,6* |
5* |
Пусть
компьютер имеет скорость вычислений
1*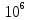 /сек,
тогда при n
= 20
/сек,
тогда при n
= 20
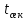 =
=
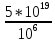 =5*
=5*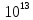 сек,
в часе – 60*60 = 3600 сек, то есть
сек,
в часе – 60*60 = 3600 сек, то есть
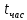 =
=
 ;
;
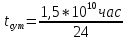 ~ 1,5*
~ 1,5* сут;
сут;
 =
=
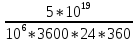 ~ 1,5 млн. лет
~ 1,5 млн. лет
Поэтому необходимы экономические методы, которые будут рассмотрены ниже.
Вычисление
обратной матрицы: матрица
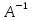 называется обратной по отношению к
исходной квадратной матрице А, если их
произведение равно единичной матрице:
А*
называется обратной по отношению к
исходной квадратной матрице А, если их
произведение равно единичной матрице:
А* =
Е=
=
Е=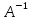 *А=Е.
Всякая невырожденная матрица А (то есть
имеющийся отличный от нуля определитель)
имеет обратную. При этом det
*А=Е.
Всякая невырожденная матрица А (то есть
имеющийся отличный от нуля определитель)
имеет обратную. При этом det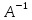 =
=
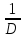 .
Пусть имеем исходную матрицу:
.
Пусть имеем исходную матрицу:
А
=

Каждый
элемент
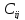 (i,j
= 1…..n)
обратной матрицы B
=
(i,j
= 1…..n)
обратной матрицы B
=
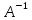 равен отношению алгебраического
дополнения
равен отношению алгебраического
дополнения
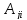 элемента
элемента
 (не
(не
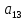 )
исходной матрицы к значению ее
определителя.
)
исходной матрицы к значению ее
определителя.
С
=
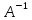 =
=

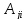 – равен минору
элемента
– равен минору
элемента
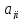 , умноженному на
, умноженному на
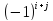 а минор элемента
а минор элемента
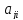 есть определитель (n-1)
порядка, образованный из определителя
матрицы A
зачеркиванием i
– строки и j
– столбца.
есть определитель (n-1)
порядка, образованный из определителя
матрицы A
зачеркиванием i
– строки и j
– столбца.
Если
подсчитать число операций, необходимое
для вычислений обратной матрицы (без
специальных методов), то оно равно: сумме
числа операций для вычисления
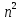 алгебраических дополнений на определитель
D
, который тоже надо вычислить.
алгебраических дополнений на определитель
D
, который тоже надо вычислить.
Таким
образом N
=
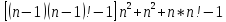 =
=
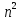 n!-1
=
n!-1
=
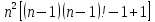 +n*n!-1
=
+n*n!-1
=
 +n*n!
– 1 =
+n*n!
– 1 =
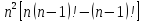
+n*n!
– 1 =
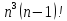 -
-
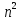 (n-1)!
+ n*n! – 1 = (n - 1)!(
(n-1)!
+ n*n! – 1 = (n - 1)!(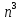 -
-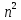 )
+ n*n!
~ (n-1)!(
)
+ n*n!
~ (n-1)!(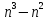 +
+
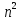 )
= (n-1)!
)
= (n-1)!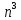 =
=
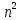 n!
n!
Рассмотрим два случая трёх уравнений:
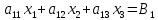
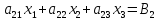
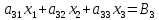
Умножим
первое уравнение на
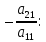
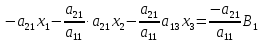
И прибавим его к уравнению второму:
Получим

После преобразования:
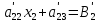
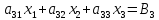
Теперь
умножим первое уравнение на
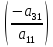 получим
получим
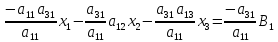
И сложим с третьим уравнением и получим

Или
нами преобразованный:
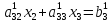
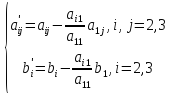
То система приобретает вид:
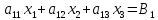
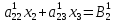
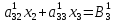
Теперь
реализуем второй этим и из третьего
уравнения исключаем
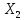 по той же методике. Для этого умножаем:
второе уравнение на
по той же методике. Для этого умножаем:
второе уравнение на
 и прибавим к третьему, получаем
и прибавим к третьему, получаем
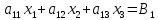
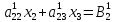

Где
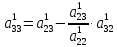 ;
;
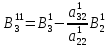
На
этом заканчивая прямой
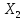
Матрица этой системы имеет треугольный вид.
Мы
видим, что в процессе исключения
переменных приходиться делать на
коэффициенты
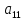 ,
,
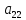 и так далее. Поэтому они должны быть
отличны от нуля. Для этого необходимо
предусмотреть в вычислительном алгоритме
перестановку уравнений системы, если
будут нулевые коэффициенты.
и так далее. Поэтому они должны быть
отличны от нуля. Для этого необходимо
предусмотреть в вычислительном алгоритме
перестановку уравнений системы, если
будут нулевые коэффициенты.
Обратный
ход начинается с решения третьего
уравнения
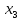 =
=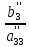 .
Далее находим
.
Далее находим
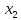 из второго уравнения:
из второго уравнения:
 =
=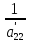 (
(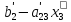 );
);
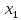 =
=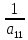 (
( )
)
Аналогично строится алгоритм для линейной системы с производным числом уравнений
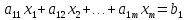
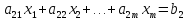
………………………………………………………
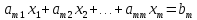
Предположим,
что
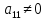 .
Поделим первое уравнение на
.
Поделим первое уравнение на
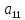 ,
получим
,
получим
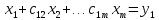 ,
где
,
где
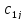 =
=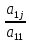 ;
j
=2,…m;
;
j
=2,…m;
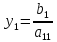 и остальные уравнения
и остальные уравнения

Исключим
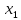 из этой системы. Для этого умножим первое
уравнение на -
из этой системы. Для этого умножим первое
уравнение на -
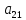 и сложим со вторым, затем первое умножаем
-
и сложим со вторым, затем первое умножаем
- и складываем с третьим и так далее …
умножаем на -
и складываем с третьим и так далее …
умножаем на -
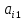 и складываем с i
– ым уравнением, в итоге получим
и складываем с i
– ым уравнением, в итоге получим
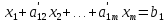
...........................................
……………………………………….
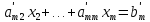
Где
 =
=
 -
-
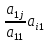 ;
;
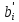 =
=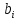 -
-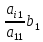
В
рассмотренной системе
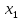 содержится только в первом уравнении,
поэтому в дальнейшем проверяем исключения
в оставшейся системе уравнений.
содержится только в первом уравнении,
поэтому в дальнейшем проверяем исключения
в оставшейся системе уравнений.
Матрица этой системы имеет вид:
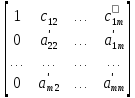
Если
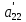 не равно нулю, то можно сделать следующий
шаг методом Гаусса, и прийти к системе
эквивалентной исходной, имеющей матрицу
типа
не равно нулю, то можно сделать следующий
шаг методом Гаусса, и прийти к системе
эквивалентной исходной, имеющей матрицу
типа
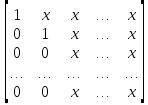
Здесь x – ненулевые элементы.
Требование
неравенства нулю диагонального элемента
тогда заменяется более жестким
требованием: из всех оставшихся в «k»-
ом столбце элементов нужно выбрать
наибольший по модулю и поставить его
на место элемента
 .
.
Заметим,
что диагональные элементы называются
ведущими
элементами.
Ведущий элемент
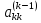 – коэффициент при «k»-
ом неизвестном в «k»-
ом уравнении на «k»-
ом шаге исключения.
– коэффициент при «k»-
ом неизвестном в «k»-
ом уравнении на «k»-
ом шаге исключения.
Благодаря выбору наибольшего по модулю элемента уменьшаются множители, используемые для преобразования уравнений, что уменьшает погрешность вычислений.
Метод
Гаусса целесообразно использовать для
решения систем с плотно заполненной
матрицей. Все элементы матрицы и правые
части уравнений находятся в оперативной
памяти машины. Число арифметических
операций примерно равно (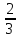 )
)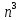 .
.
Рассмотрим пример:

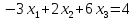

Исключим
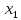 из второго и третьего уравнений. Для
этого умножим первое уравнение на 0,3 и
прибавим ко второму, а затем первое
умножим на (-0,5) и прибавим к третьему.
Получим:
из второго и третьего уравнений. Для
этого умножим первое уравнение на 0,3 и
прибавим ко второму, а затем первое
умножим на (-0,5) и прибавим к третьему.
Получим:
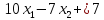

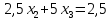
Прежде
чем исключить
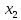 из третьего уравнения, обратим внимание
на то, что коэффициент при
из третьего уравнения, обратим внимание
на то, что коэффициент при
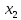 ,
равный -0,1 – мал. Поэтому лучше переставить
уравнения 2 и 3. Однако пока мы проведем
сейчас вычисления без ограничений на
разряды, поэтому продолжим.
,
равный -0,1 – мал. Поэтому лучше переставить
уравнения 2 и 3. Однако пока мы проведем
сейчас вычисления без ограничений на
разряды, поэтому продолжим.
Умножим второе уравнение на 2,5 и сложим с третьим:
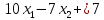

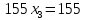
Это прямой ход. Осуществим обратный ход:
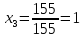 ;
;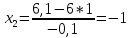 ;
;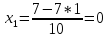
Подстановкой
в исходную систему и убедимся, что это
есть точное решение. То есть при таких
вычислениях малость коэффициентов при
 не влияет, но на практике всегда
приходиться округлять.
не влияет, но на практике всегда
приходиться округлять.
Рассмотрим теперь слегка измененную систему, но с тем же решением:
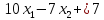

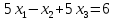
Здесь
изменения только во втором уравнении,
слегка изменен коэффициент при
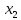 и правая часть. Опять осуществим прямой
ход, но при этом будем считать, что
проводим расчет в рамках
арифметики с плавающей запятой, сохраняя
лишь пять разрядов.
и правая часть. Опять осуществим прямой
ход, но при этом будем считать, что
проводим расчет в рамках
арифметики с плавающей запятой, сохраняя
лишь пять разрядов.
Умножим первое уравнение на 0,3 и сложим со вторым, а затем на 0,5 и сложим с третьим. После первого шага исключения получим
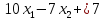
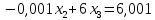
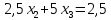
Допустим
мы, несмотря на малость члена при
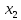 и не переставляя уравнения, продолжим
исключение
и не переставляя уравнения, продолжим
исключение
 .
Для этого мы вынуждены уравнение,
умножив на 2500. При умножении получим
число 15002,5, которое нужно округлить до
5 разрядов. В результате получим третье
уравнение в виде: 1500
.
Для этого мы вынуждены уравнение,
умножив на 2500. При умножении получим
число 15002,5, которое нужно округлить до
5 разрядов. В результате получим третье
уравнение в виде: 1500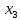 =15004;
отсюда
=15004;
отсюда
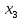 =
=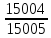 =0,99993.
Из второго и первого уравнений получим
=0,99993.
Из второго и первого уравнений получим
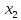 =
= =
=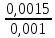 =
-1,5
=
-1,5
 =
=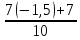 =-0,35
=-0,35
То
есть точное решение
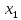 =0;
=0;
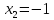 ;
;
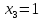 ,
а получим
,
а получим
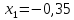 ;
;
 ;
;
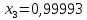
Итак, малая величина ведущего элемента привела к большим погрешностям.
В подтверждение этому переставим уравнения системы
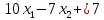
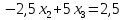
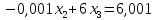
Исключим
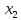 из третьего уравнения, умножив второе
на 0,0004 и сложив с третьим:
из третьего уравнения, умножив второе
на 0,0004 и сложив с третьим:
6,002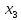 =6.002
=6.002
Отсюда:
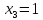 ;
;
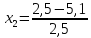 =-1;
=-1;
 =
=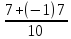 =0,
то есть получим точное решение.
=0,
то есть получим точное решение.
Обсуждение погрешностей
Вычисленное
по методу Гаусса решение
 ,
отличается от точного решения матричного
уравнения X=
,
отличается от точного решения матричного
уравнения X=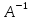 B
из за погрешностей округления. Существует
две величины, характеризующие степень
отклонения точного решения от
приближенного. ɛ = x-
B
из за погрешностей округления. Существует
две величины, характеризующие степень
отклонения точного решения от
приближенного. ɛ = x-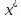 ,
r
– равна разности между правой и левой
частями уравнений при подстановке в
них решения:
,
r
– равна разности между правой и левой
частями уравнений при подстановке в
них решения:
r
=B-
A -называется
невязкой
-называется
невязкой
При
ɛ 0
обычно r~0,
но обратное справедливо не всегда, в
частности для плохо обусловленных
систем.
0
обычно r~0,
но обратное справедливо не всегда, в
частности для плохо обусловленных
систем.
Если система не является плохо обусловленной, то в практических расчетах контроль точности решения осуществляется с помощью невязки.
Расчет определителя и обратной матрицы.
Обычно матрица приводится к треугольному виду с использованием прямого хода метода Гаусса. В процессе исключения элементов величина определителя не меняется. Знак определителя меняется на противоположный при перестановке его столбцов или строк.
После приведения матрицы А к треугольному виду ее определитель равен произведению диагональных элементов:
Det
A = ±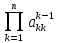
Здесь
диагональные элементы
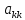 берутся из преобразованной, а не исходной
матрицы. Знак зависит от того, четная(+)
или нечетная(-) была суммарная перестановка
строк(или столбцов) матрицы при ее
приведении к треугольной форме(для
получения ненулевого или максимального
по модулю элемента). По методу исключения
можно вычислять определители 100 и
большего порядков.
берутся из преобразованной, а не исходной
матрицы. Знак зависит от того, четная(+)
или нечетная(-) была суммарная перестановка
строк(или столбцов) матрицы при ее
приведении к треугольной форме(для
получения ненулевого или максимального
по модулю элемента). По методу исключения
можно вычислять определители 100 и
большего порядков.
Найдем
обратную матрицу
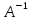 .
Обозначим ее элементы
.
Обозначим ее элементы
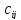 .
Запишем равенство А
.
Запишем равенство А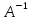 =Е
в виде
=Е
в виде
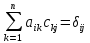 ,
,
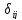 =
= i,
j
= 1,2…n
i,
j
= 1,2…n
Таким
образом, чтобы найти элементы j
столбца
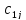 ,
,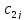 ….
….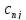 нужно решить систему уравнений
нужно решить систему уравнений

Следовательно для обращения матрицы нужно «n» раз такую систему уравнений при j = 1,2,3…….n.