
Набор лекций по Выч. математике ч 1
.docxПоскольку матрица системы не меняется, то при исключении неизвестных при методе Гаусса прямой ход проводится только один раз.
Для каждой системы делается легко обратный ход после несложных преобразований с использованием правых частей систем вида последнего примера.
Этот способ требует только в три раза больше действий, чем при решении одной системы уравнений- метод прогонки. Это модификация метода Гаусса для случая разреженных (трех диагональных) матриц. Они получаются при моделировании некоторых инженерных задач, а также при численном решении некоторых краевых задач для дифференциальных уравнений.
Запишем систему уравнений в виде



……………………………………………


Метод прогонки можно применять, если знаменатели выражений (n) не равны нулю. Для этого должны выполняться условия (это доказывается):

 ≥
≥
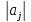 +
+ (хотя
бы для одного j
должно быть строгое неравенство), для
j
= 1,2,…..n-1
– система имеет единственное и устойчивое
решение.
(хотя
бы для одного j
должно быть строгое неравенство), для
j
= 1,2,…..n-1
– система имеет единственное и устойчивое
решение.
 Все эти коэффициенты могут быть
комплексными.
Все эти коэффициенты могут быть
комплексными.
Другие прямые методы.
Метод квадратного корня (для симметричных матриц); Клеточные методы (для решения больших систем)
Итерационные методы.
Часть применяются, чтобы уточнить решение, полученное с помощью прямого метода (погрешности возникают из-за округления и иногда могут быть значительными).
Рассмотрим один из методов, позволяющий уточнять решение, полученное прямым методом.
Пусть имеем систему линейных уравнений:


…….…………………………… (1)
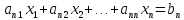
Пусть
с помощью некоторого прямого метода
вычислили приближенные значения
неизвестных:
 Если мы их подставим в левые части (1)
получим справа некоторые значения
Если мы их подставим в левые части (1)
получим справа некоторые значения
 ,
отличные от
,
отличные от
 (i=1,2,…n):
(i=1,2,…n):


….…..………………………………… (2)

Введем обозначения:
 -
погрешности значений неизвестных
-
погрешности значений неизвестных
 -
невязки
i=1,2,…n
-
невязки
i=1,2,…n
Вычтем каждое уравнение системы (1) из соответствующего уравнения системы (2), с учетом введенных обозначений получим:
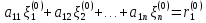

….…..………………………………… (3)

Решаем
эту систему, находим погрешности
 ,
которые используются в качестве поправок
к решению и тогда в первом приближении
будем иметь:
,
которые используются в качестве поправок
к решению и тогда в первом приближении
будем иметь:
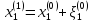 ;
;

Теперь
эти решения можно опять подставить в
исходную систему уравнений и найти
новые поправки
 ,
…
,
…
 и решения второго приближения:
и решения второго приближения:
 =
= +
+ ,
,
 =
= +
+ ,
…..
,
….. =
= +
+ .
Процесс продолжается до тех пор пока
погрешности(поправки)
.
Процесс продолжается до тех пор пока
погрешности(поправки)
 не станут достаточно малыми. Это и есть
итерационный метод.
не станут достаточно малыми. Это и есть
итерационный метод.
Поскольку при
итерациях используется одна
и та же матрица коэффициентов
с элементами
 ,
а меняются только правые части исходной
системы, то можно строить экономические
алгоритмы.
,
а меняются только правые части исходной
системы, то можно строить экономические
алгоритмы.
Например, при использовании метода Гаусса сокращается объем вычислений на этапе прямого хода.
Иногда в программе вместо задания разных значений двух последовательных приближений, задается допустимое число итераций, при достижении которого счет просто прекращается.
Метод Гаусса – Зейделя. Один из самых распространенных итерационных методов, отличается простотой и легкостью программирования.
Проиллюстрируем на примере:

 (4.25)
(4.25)

Пусть
диагональные элементы
 -
отличны от нуля, в противном
случае можно поменять.
Выразим неизвестные
-
отличны от нуля, в противном
случае можно поменять.
Выразим неизвестные
 ,
,
 ,
,
 соответственно
из уравнений
соответственно
из уравнений



Зададим
некоторые начальные (нулевые) приближения
значений неизвестных:
 ,
,
 ,
,
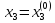 .
Подставляя эти значения в правую часть
(4.26) получаем первое приближение для
.
Подставляя эти значения в правую часть
(4.26) получаем первое приближение для
 :
:

Используя
это выражение для
 и приближение
и приближение
 для
для
 .
Находим из (4.27) приближение для
.
Находим из (4.27) приближение для
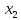 :
:

Наконец,
используя вычисленные значения
 ,
,
 ,
находим с помощью (4.28) первое приближение
уравнения
,
находим с помощью (4.28) первое приближение
уравнения
 :
:

На этом заканчивается первая итерация решения системы.
Используя теперь
значения
 ,
,
 ,
, можно аналогично провести вторую
итерацию, в результате которой будут
найдены вторые приближения:
можно аналогично провести вторую
итерацию, в результате которой будут
найдены вторые приближения:
 ,
,
 ,
, .
.
Приближение с номером k можно представить в виде



Итерационный
процесс продолжается до тех пор пока,
значения
 ,
,
 ,
,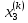 не станут близкими с заданной погрешностью
к значениям
не станут близкими с заданной погрешностью
к значениям
 ,
,
 ,
, .
.
Рассмотрим теперь
систему n
– уравнений с n-
неизвестными
 , i=1,2,…n.
, i=1,2,…n.
Будем опять полагать, что все диагональные элементы отличны от 0. Тогда в соответствии с методом приближение k-оe можно представить в виде.

i = 1,2,…n
Критерий окончания итерационного процесса можно записать в виде
δ
= max
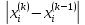 < ɛ - по max
абсолютного отклонения
< ɛ - по max
абсолютного отклонения
1 ≤ i ≤ n
Или
в виде (при
 >>1):
>>1):
max
 < ɛ - критерий по относительным разностям
< ɛ - критерий по относительным разностям
Для сходимости итерационного процесса достаточным условием является:
 ; i =
1,2,…n.
; i =
1,2,…n.
То есть для каждого уравнения системы модуль диагонального элемента был не меньше суммы модулей всех остальных коэффициентов. При этом хотя бы для одного уравнения это условие должно выполняться строго.
Это условие не является необходимым, так как для некоторых итерации сходятся и при нарушении этого условия.
Задачи на собственные значения
Большое количество научно – технических задач связано с нахождением собственных значений и собственных векторов матриц.
Пусть имеем квадратную матрицу «n» - го порядка
A=
Характеристической матрицей G данной матрицы A называется матрица вида
C
= A – λE= ,
,
где λ – собственное значение, Е – единичная матрица.
Определитель матрицы С называется «характеристическим многочленом» и может быть представлен в виде:
det
C =

Корни этого многочлена и являются собственными значениями.
Вектор
Х =
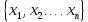 ,
соответствующий некоторому собственному
значению λ
и удовлетворяющий условию
,
соответствующий некоторому собственному
значению λ
и удовлетворяющий условию
AX = λС
называется собственным вектором матрицы А.
Матричное уравнение можно представить в виде:


…….……………………………

Эта
система имеет ненулевые решения лишь
тогда, когда det
(a
- λE)=0,
то есть определитель матрицы, которая
получается если λ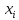 перенести влево.
перенести влево.
Отметим, что собственные значения треугольной матрицы равны ее диагональным элементам.
Число
обусловленности
линейных алгебраических систем. Пусть
имеем систему АХ = Bμ;
A
– невырожденная матрица коэффициентов
n*n.
Пусть правая часть получила приращение
∆b.
Если x
решение, то x+∆x
будет решением A(x+∆x)
= b+∆b.
Можно показать,
что между относительными погрешностями
вектора свободных членов
 и вектора решения
и вектора решения

Существует связь:
 (2)
(2)
Число
обусловленности Cond
A=
 -
является коэффициентом этой связи. –
легко показать,
что cond
A
служит также коэффициентом роста
относительных погрешностей при неточном
задании элементов матрицы А в (1):
-
является коэффициентом этой связи. –
легко показать,
что cond
A
служит также коэффициентом роста
относительных погрешностей при неточном
задании элементов матрицы А в (1):
 и
и

Таким образом чем больше «CondA», тем сильнее сказываются на решении линейной системы ошибки в исходных данных.
Если CondA – велико – система плохо обусловлена
Если CondA – мало – хорошо обусловлена
Говорить «хорошо или плохо» в отрыве от контекста задачи бессмысленно. Здесь играет роль – размерность задачи, требуемая точность, точность представления чисел в ЭВМ и так далее.
Однако можно дать оценку снизу:
Cond
A=
 ≥
≥
Оценкой
снизу меры обусловленности может служить
число обусловленности Тодди =
 ,
где
,
где
 ,…
,…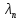 собственные числа матрицы А, упорядоченные
по модулю.
собственные числа матрицы А, упорядоченные
по модулю.
Непосредственный расчет числа обусловленности может быть особенно, при большой размерности трудной задачи. Поэтому часть судят по достаточным признакам(пример – преобладание диагональных элементов) либо по приближении dA алгоритмов .
Проблема собственных значений
Часто встречается в научно – технических задачах.
Пусть имеем систему уравнений


…….……………………………

A= ;
AX = 0
;
AX = 0
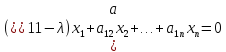
 (A-
(A- )X=0
)X=0
………….………..……………………
AX =


Чтобы
эта система имела решение det(A- )=0;
det(A-
)=0;
det(A- )
=
)
=
 .
Каждому значению λ
будет соответствовать набор значений
.
Каждому значению λ
будет соответствовать набор значений
 .
Каждое значение λ
называется собственным значением
матрицы А. Каждому собственному значению
соответствует собственный вектор Х(
.
Каждое значение λ
называется собственным значением
матрицы А. Каждому собственному значению
соответствует собственный вектор Х( )
матрицы А.
)
матрицы А.
Для симметричных матриц собственные значения совпадают с диагональными элементами.
Нелинейные уравнения
Пусть имеем уравнение (нелинейное) вида: F(x)=0, F(x) – некоторая непрерывная функция. Необходимо найти его корни. Нелинейные уравнения можно разделить на два класса: алгебраические и трансцендентные.
Алгебраические – содержат только алгебраические функции (целые, рациональные, иррациональные) – в частности – многочлен является целой алгебраической функцией.
Трансцендентные – содержат тригонометрические, показательные, логарифмические функции.
Методы решения делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного отношения (формулы) (до 4-ой степени включительно, если 5-я степень в взять невозможно).
Итерационные методы (то есть методы последовательных приближений) состоят из двух этапов
а) отыскание приближенного значения корня или содержащего его отрезка;
б) уточнение приближенного значения до заданного уровня точности.
Мы рассмотрели случаи только вещественного решения нелинейных уравнений(функция меняет знак).
Метод деления отрезка пополам:
Допустим,
что удалось найти отрезок
 ,
в котором расположено значение
корня x=c,
то есть a<c<b.
Берем в качестве начального приближения
корня середину отрезка, то есть
,
в котором расположено значение
корня x=c,
то есть a<c<b.
Берем в качестве начального приближения
корня середину отрезка, то есть
 .
Далее смотрим на значения F(x)
в точках a,
.
Далее смотрим на значения F(x)
в точках a, ,b.
Тот отрезок, на котором F(x)
принимает значения разных знаков,
содержит искомый корень, поэтому его
принимаем за новый отрезок и делим его
пополам и так далее. Таким образом после
каждой итерации отрезок, на котором
содержится корень, уменьшается вдвое.
,b.
Тот отрезок, на котором F(x)
принимает значения разных знаков,
содержит искомый корень, поэтому его
принимаем за новый отрезок и делим его
пополам и так далее. Таким образом после
каждой итерации отрезок, на котором
содержится корень, уменьшается вдвое.
Итерационный
процесс продолжается до тех пор, пока
значение F(x)
после n
– ой итерации не станет меньше по модулю
некоторого заданного малого числа ɛ ,
то есть
 <ɛ.
<ɛ.
Этот метод медленный, но всегда сходится , то есть решение получается всегда, причем с заданной точностью.
Метод хорд:
Пусть
мы нашли отрезок
 ,
на котором F(x)
меняет знак. Пусть для определенности
F(a)>0,
F(b)<0.
Процесс итераций заключается в том, что
в качестве приближений к корню принимаются
значения
,
на котором F(x)
меняет знак. Пусть для определенности
F(a)>0,
F(b)<0.
Процесс итераций заключается в том, что
в качестве приближений к корню принимаются
значения
 …точек
пересечения хорды с осью абсцисс. Сначала
находим уравнение хорды АВ:
…точек
пересечения хорды с осью абсцисс. Сначала
находим уравнение хорды АВ:
 ,
чтобы найти точку пересечения, положим
x=0.
Следовательно
,
чтобы найти точку пересечения, положим
x=0.
Следовательно
 F(a)+a;
x=
F(a)+a;
x= F(a)+a;
F(a)+a;
 +
+ ;
Далее сравниваем F(a)
и F(
;
Далее сравниваем F(a)
и F( )
– дл рассматриваемого случая корень
будет находиться в интервале (a,
)
– дл рассматриваемого случая корень
будет находиться в интервале (a, ),
так как F(
),
так как F( )<0.
Отрезок (
)<0.
Отрезок ( )
– отбрасываем и так далее.
)
– отбрасываем и так далее.
Итерационный
процесс продолжается до тех пор, пока
 <ɛ
<ɛ
Метод был быстр, чем предыдущий и его успех гарантирован.
Метод Ньютона
(касательных).
По сути дела аналогичен методу секущих.
Только здесь вместо хорды на k-ой
итерации проводится касательная к
правой y
= F(x)
при x= и ищется точка пересечения касательной
с осью абсцисс. Уравнение касательной
в точке
и ищется точка пересечения касательной
с осью абсцисс. Уравнение касательной
в точке
 с координатами F(
с координатами F( ),
),
 имеет вид:
имеет вид:
y
- F( )=
)=

Далее
все повторяется: находим уравнение
касательной в точке
 ,
находим точку пересечения этой касательной
с осью x:
-
,
находим точку пересечения этой касательной
с осью x:
- и так далее.
и так далее.
Формула для (n+1)-го приближения имеет вид:

При
этом естественно необходимо,
чтобы
 ≠0.
Для окончания итерационного процесса
может быть использовано условие
≠0.
Для окончания итерационного процесса
может быть использовано условие
 <ɛ
или условие близости двух последовательных
приближений.
<ɛ
или условие близости двух последовательных
приближений.

Мы видим, что здесь не нужно искать интервал, где есть корень уравнения. На каждой итерации объем вычислений больше, чем в предыдущих методах, но сходится он быстрей. Например после 5-6 итераций погрешность метода может быть такой же как у предыдущих после 50 итераций.
Трудность в применении метода Ньютона состоит в выборе начального приближения, для поиска которого иногда целесообразно применить всегда сходящийся метод (например, деления отрезка пополам).
Рассмотренные выше методы применимы для решения как трансцендентных, так и алгебраических уравнений, однако, алгебраические уравнения имеют некоторые особенности, которые могут быть использованы при их решении.
Решение алгебраических уравнений.
Пусть имеем алгебраическое уравнение (с действительными коэффициентами) вида:
 (5.5)
(5.5)
Его свойства:
-
количество корней равно «n» (могут быть комплексные и действительные);
-
комплексные корни образуют комплексные сопряженные пары: x = c ± id;
-
число положительных действительных корней меньше или равно числу перемен знаков в последовательности коэффициентов
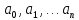 .
.
Заменяя x на –x в (5.5) таким же образом можно оценить число отрицательных корней.
Рассмотрим применение метода Ньютона к решению уравнения (5.5).
Как мы видим итерационный процесс в этом методе имеет вид:

F( )
=
)
= ;
;
 .
.
Для вычисления значений этих многочленов может быть использована схема Горнера. Естественно при использовании метода Ньютона должны выполняться условия сходимости.
После нахождения какого либо корня x=у _____ можно разделить на (x-e), понизив его порядок. Однако следует помнить, что даже небольшая погрешность в значении первого корня может привести к накапливанию погрешности в дальнейших вычислениях.
Системы линейных уравнений:
Пусть имеем систему:
 ….
….

 (5.8)
(5.8)
_ _ _ _ _ _ _ _ _ _ _ _

Не существует прямых (в отличие от линейных уравнений) методов решения этих систем. Обычно используют итерационные методы:
а) метод простой итерации (напоминает метод Гаусса-Зейделя для линейных уравнений).
Представим (5,8) в виде:
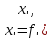



_ _ _ _ _ _ _ _ _ _ _ _ _ _


Пусть
в результате предыдущей итерации
получены значения неизвестных

 Тогда для неизвестных на следующей
итерации можно записать:
Тогда для неизвестных на следующей
итерации можно записать:
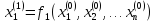

………………………………………..

…………………………………………

Итерационный
процесс продолжается до тех пока значения
неизвестных в двух последовательных
итерациях не станут достаточно малыми,
__ C
Здесь успех определяется удачным выбором численных приближений. В противном случае итерационный процесс может не сойтись.
б) метод Ньютона. Обладает более быстрой сходимостью.
Пусть имеем значения
неизвестных на предыдущей итерации
 .
Задача состоит в нахождении приращений
(поправок) к этим значениям: ∆
.
Задача состоит в нахождении приращений
(поправок) к этим значениям: ∆ ,
∆
,
∆ ,…
∆
,…
∆ ,
благодаря которым решение системы
запишется в виде:
,
благодаря которым решение системы
запишется в виде:
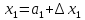 ,
,
 ,….
,…. .
(5.10)
.
(5.10)
C этой целью проведем разложение левых частей уравнения (5.8) с учетом (5.10) в ряд Тейлора, ограничиваясь лишь линейными членами, относительно этих приращений.
Метод простой итерации
F(x)=0; x=f(x)
x
Пусть известно
начальное приближение x= ,
подставим в правую часть:
,
подставим в правую часть:

Теперь
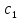 подставляем в правую часть
подставляем в правую часть
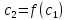 и так далее , до
того пока
и так далее , до
того пока
 даст условие сходимости:
даст условие сходимости:

Начальное приближение
должно находиться в окрестности D(есть
теорема). Если начальное приближение
находится в окрестности D
корня, то в методе Ньютона последовательность
 сходится к значению корня с.
сходится к значению корня с.
Иногда целесообразно применять смешанный алгоритм. ______ и используется всегда сходящийся метод (например – деление отрезка пополам), а затем быстрее метод Ньютона.
Целая
рациональная функция – (многочлен):
 .
.
Дробно рациональная функция – отношение многочленов.
Иррациональная функция – корни из многочленов(дробные степени).

Полагаем
F(x)
= 0; отсюда тогда пересечения x-c,
касательной с, осью x
будет F( )+
)+



……………………………………………………………………

Приравнивая
нулю правые части, получим систему
линейных уравнений относительно
приращений
 .
.


……………………………………………….. (5.11)

Значения
 и
и
 – вычисляются при
– вычисляются при
 ,
, ….
…. .
.
Определителем системы (5.11) является:
J
=
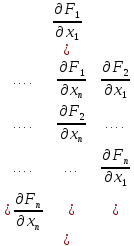
Для
существования единственности решения
он должен быть ≠0 на каждой итерации.
Счет прекращается, когда max .
В методе Ньютона важен удачный
выбор начального
приближения. Сходимость ухудшается
с ростом
числа уравнений системы.
.
В методе Ньютона важен удачный
выбор начального
приближения. Сходимость ухудшается
с ростом
числа уравнений системы.
