
Лабораторное задание 4
.docЗадание 4.
Вычисление определенных интегралов.
Цель задания.
Знакомство с простейшими квадратурными формулами и практика в их использовании.
Содержание задания.
1. Изучение прстейших квадратурных формул.
2. Составление программы и ее отладка.
3. Решение на ЭВМ конкретной задачи, связанной с приближенным вычислением интегралов.
Постановка задачи.
С использованием
ЭВМ вычислить с точностью
![]() значение
значение
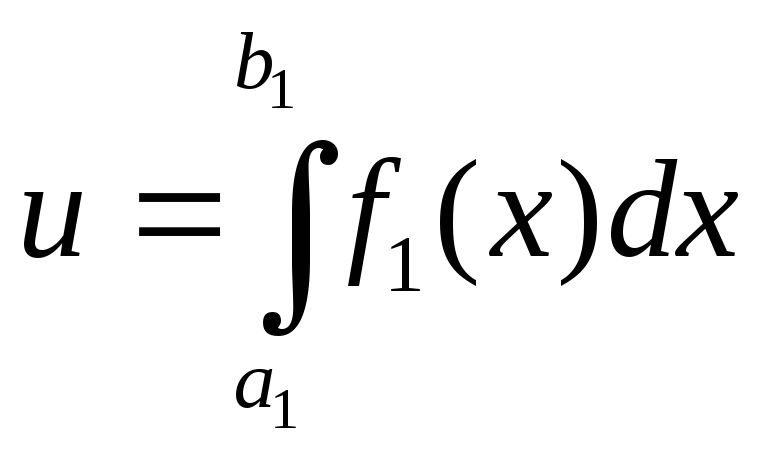
а также получить таблицу значений функции

вычисленных с
точностью
![]() в точках
в точках
![]() =
c+iH
(i=0,1,...m),
где
H=(d-c)/m.
=
c+iH
(i=0,1,...m),
где
H=(d-c)/m.
Функции
![]() ,
вещественные значения
,
вещественные значения
![]() и целое м определяются вариантом
задания (см. Приложение 1).
и целое м определяются вариантом
задания (см. Приложение 1).
Для вычисления значения определенного интеграла
![]()
с заданной точностью
![]() использовать квадратурную формулу вида
использовать квадратурную формулу вида
![]()
где
![]() ,
а
,
а
![]() и
и
![]() определяются квадратурной формулой.
Применяемая квадратурная формула также
определяется вариантом задания (см.
Приложение 1).
определяются квадратурной формулой.
Применяемая квадратурная формула также
определяется вариантом задания (см.
Приложение 1).
Для достижения требуемой точности при вычислении интеграла по квадратурной формуле использовать метод последовательного удвоения числа шагов.
Требования к программе.
1. Алгоритм вычисления
значения определенного интеграла с
задаваемой точностью
![]() должен
быть оформлен в виде описания процедуры.
должен
быть оформлен в виде описания процедуры.
2. В программе должны использоваться процедуры-функции для вычисления значений фигурирующих в задании подынтегральных функций.
3. Значения
![]() и
и
![]() (начальное
число шагов при счете по квадратурной
формуле) могут быть зафиксированы при
составлении программы; значения
(начальное
число шагов при счете по квадратурной
формуле) могут быть зафиксированы при
составлении программы; значения
![]() должны
вводиться в процессе выполнения
программы.
должны
вводиться в процессе выполнения
программы.
4. В качестве результата на печать должно быть выдано: значение
![]() ,
последовательность значений
,
последовательность значений
![]() и соответствующая последовательность
значений
и соответствующая последовательность
значений
![]() .
.
Содержание отчета.
1. Постановка задачи для конкретного варианта.
2. Алгоритм решения задачи в виде программы.
3. Полученные на ЭВМ результаты решения задачи.
Приложение 1. Варианты задания.
I. Квадратурная формула.
1) Формула прямоугольников:
![]()
где
![]()
Остаточный член:
![]()
![]()
2) Формула трапеции:
![]()
где
![]()
Остаточный член:
![]()
![]()
3) Формула Симпсона (парабол):
![]() где
где
![]() ,
N-четное.
,
N-четное.
Остаточный член:
![]()
![]()
II.
Функция
![]() ,
значения
,
значения
![]() .
.
-
N
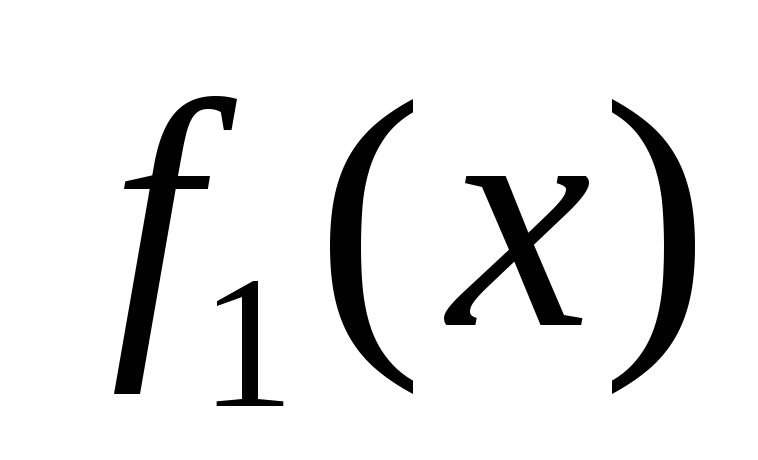
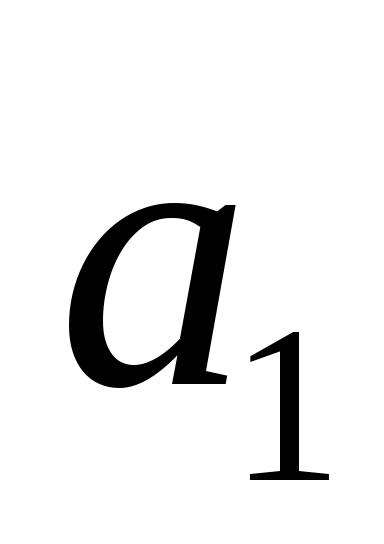
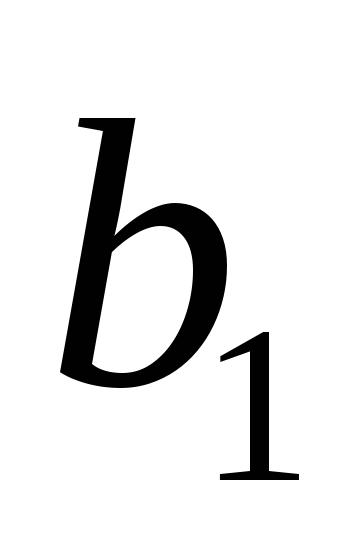
1
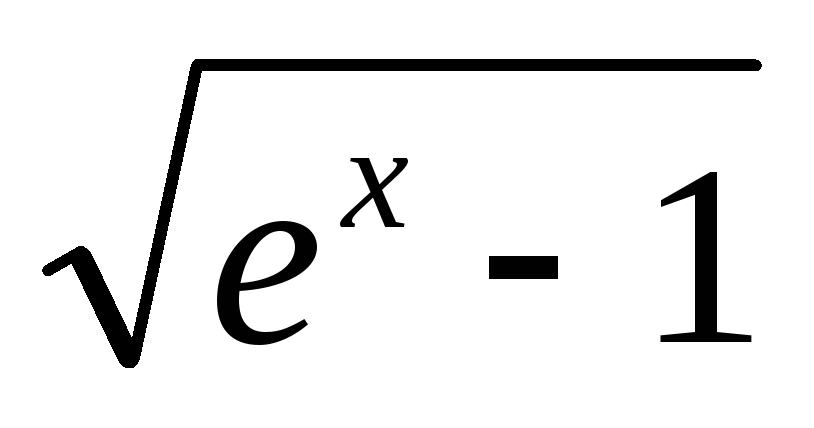
0.1
2
2

0
π
3
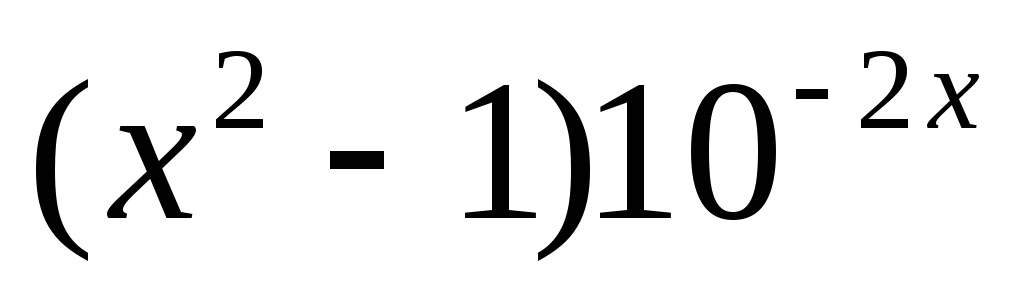
0
1
4

1
9
5
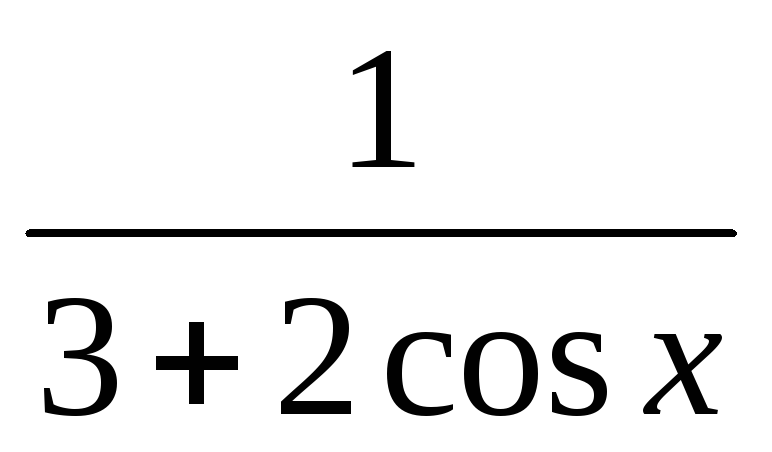
0
π
6
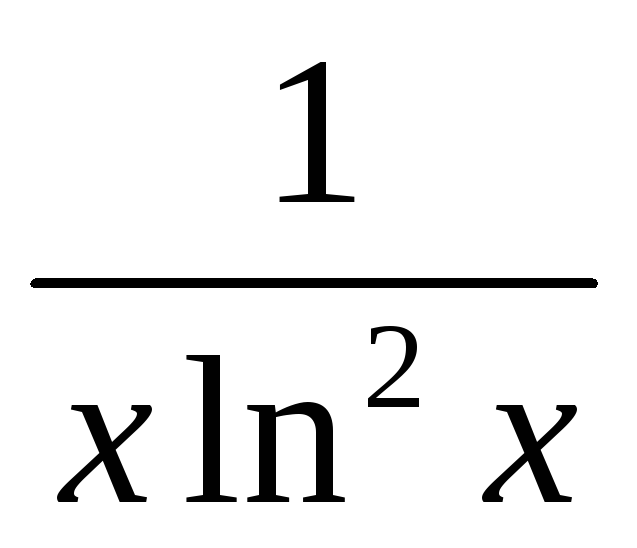
2
3
7

0.2
0.3
8
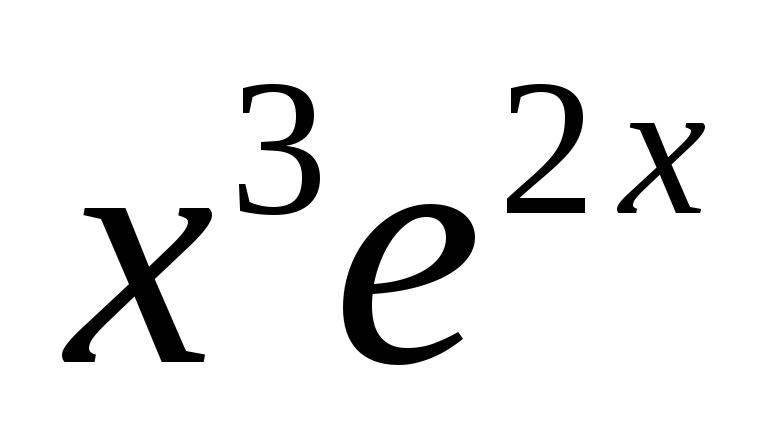
0
1
9
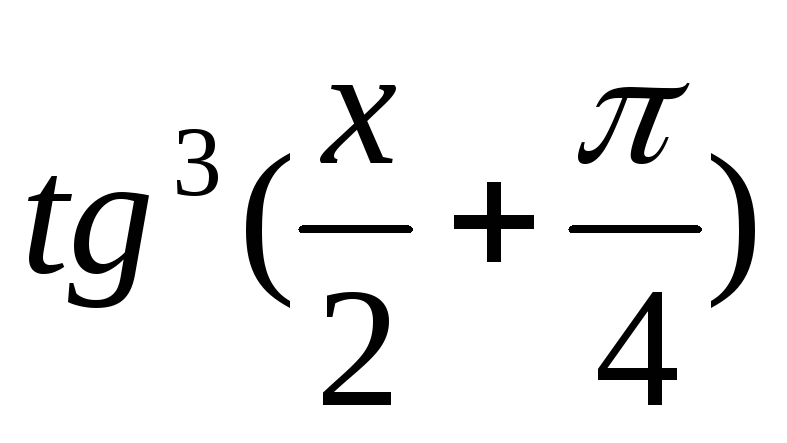
0
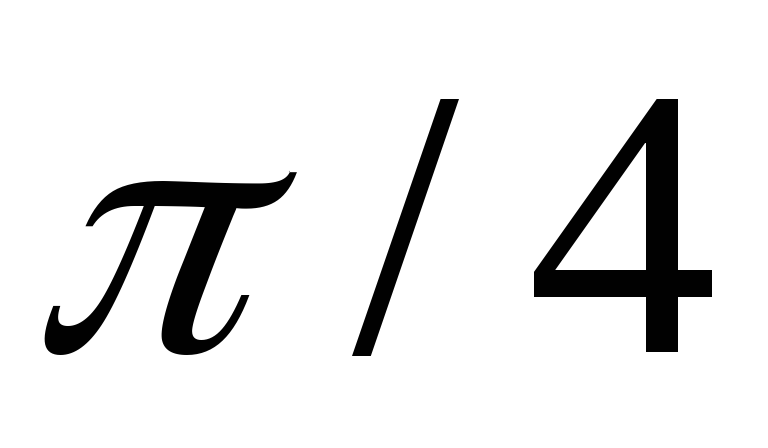
10
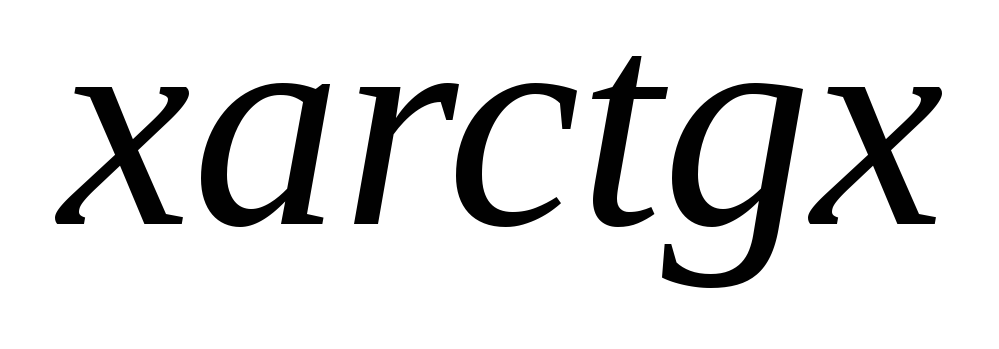
0
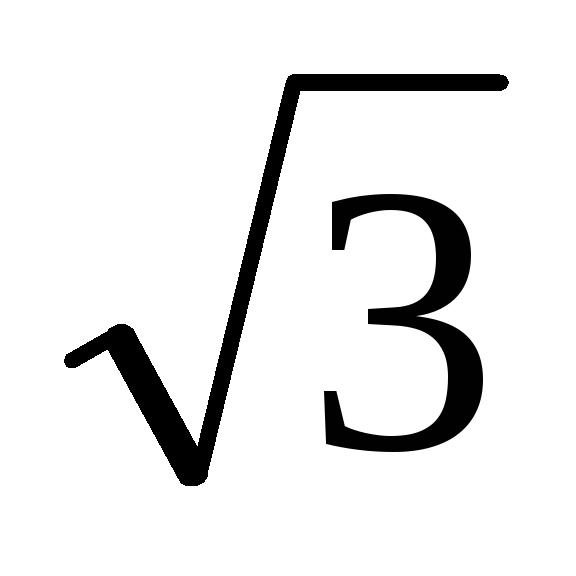
11
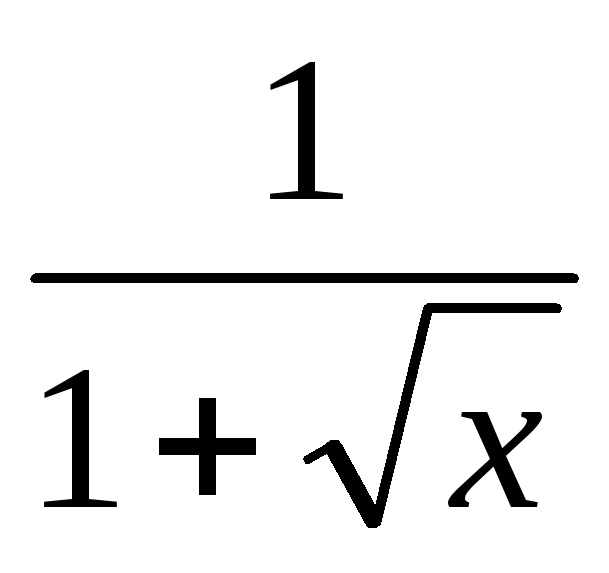
0
4
12

0
2π
13
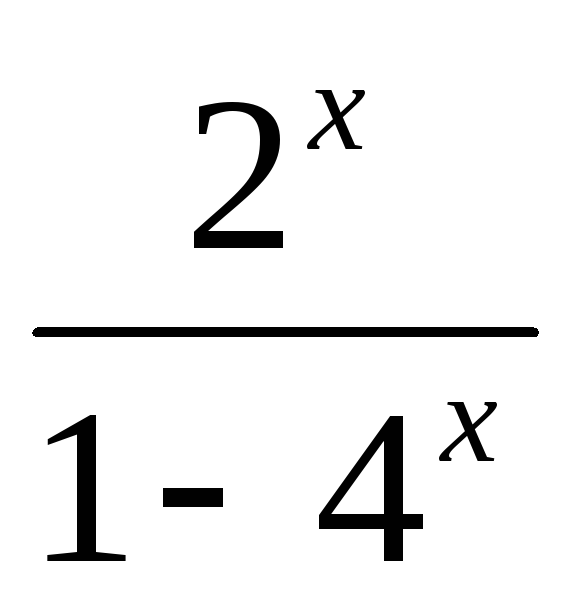
-2
-1
14
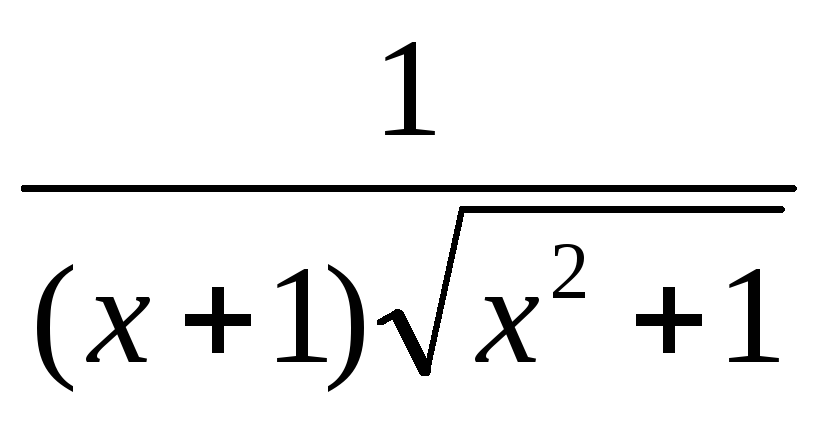
0
3/4
III.
Функция
![]() .
.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
11)
;
11)
![]() ;
12)
;
12)
![]() ;
13)
;
13)
![]() ;
14)
;
14)
![]() ;
15)
;
15)
![]()
IV.
Функция
![]() .
.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() .
.
V. Значение μ.
1) -0.01; 2) -0.05; 3) 0.05; 4) 0.01.
VI.
Значения
![]() .
.
-
N
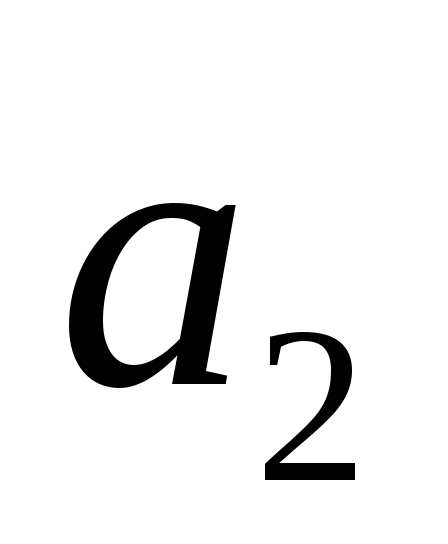
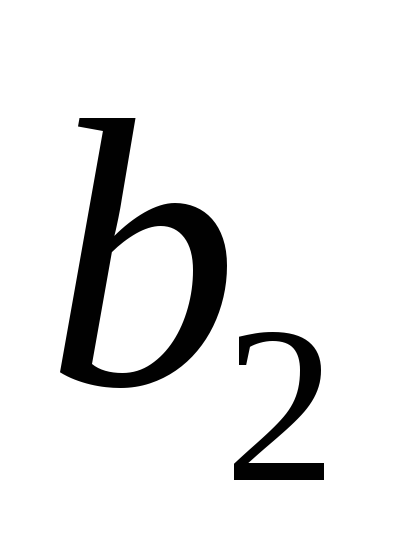
c
d
m
1
0
π/2
0.5
1.5
10
2
0
1
1
2
20
3
π/4
3π/4
1
2.5
15
4
0.5
1.5
2
3
10
Приложение 2. Методические указания
1. Для обеспечения требуемой точности при приближенном вычислении значения интеграла по квадратурной формуле нужно выбрать соответствующее значение шага h (или, что то же самое, число шагов N, на которое делится отрезок интегрирования). Для этого можно воспользоваться формулой остаточного члена квадратурной формулы, однако, оценка значения соответствующей производной подынтегральной функции, которая входит в формулу остаточного члена, нередко вызывает большие трудности. Кроме того, эту оценку приходится делать для каждой новой подынтегральной функции.
На практике для достижения требуемой точности вычисления интеграла по квадратурной формуле часто используется метод последовательного удвоения числа шагов, который заключается в следующем.
Интеграл I
вычисляется по квадратурной формуле
дважды: сначала при числе шагов, равном
N,
а затем при числе шагов равном 2N.
Погрешность
![]() приближенного значения интеграла
приближенного значения интеграла
![]() ,
вычисленного
по квадратурной формуле при числе шагов,
равном n,
определяется
приближенно по правилу Рунге:
,
вычисленного
по квадратурной формуле при числе шагов,
равном n,
определяется
приближенно по правилу Рунге:
![]()
( для формул
прямоугольников и трапеций
![]() ,
для формулы Симпсона
,
для формулы Симпсона
![]() ).
).
Таким образом,
![]() вычисляется
для последовательных значений
вычисляется
для последовательных значений
![]() и т.д., где
и т.д., где
![]() -
начальное число шагов. Процесс вычислений
заканчивается, когда для очередного
значения n
получена
погрешность
-
начальное число шагов. Процесс вычислений
заканчивается, когда для очередного
значения n
получена
погрешность
![]() .
Начальное число шагов
.
Начальное число шагов
![]() следует выбирать от 10 до 50.
следует выбирать от 10 до 50.
2. Для получения достаточно эффективной программы следует учесть, что в формулах трапеций и Симпсона при удвоении числа шагов нет необходимости вычислять значение подынтегральной функции заново во всех узлах сетки, так как все узлы сетки, полеченные при числе шагов, равном n, являются узлами сетки и при числе шагов, равном 2N.
3. Для упрощения
процедуры вычисления значения интеграла
в ней не следует предусматривать
зависимость подынтегральной функции
от каких-либо параметров. Поэтому при
описании функции
![]() параметр t
целесообразно
представить глобальной величиной.
параметр t
целесообразно
представить глобальной величиной.
4. Для отладки процедуры интегрирования следует выбрать такую подынтегральную функцию и пределы интегрирования, чтобы ответ был известен заранее и вычисление интеграла не требовало больших затрат машинного времени. Следует, однако, позаботится о том, чтобы для этой функции на самом деле реализовывался процесс последовательного удвоения числа шагов для получения результата с заданной точностью.
5. Следует обратить
внимание на то, что некоторые ошибки в
программе при реализации метода удвоения
числа шагов (например, учет лишнего узла
![]() )
не сказываются на точности получаемого
результата, но эта точность достигается
за счет дополнительных затрат машинного
времени.
)
не сказываются на точности получаемого
результата, но эта точность достигается
за счет дополнительных затрат машинного
времени.
![]()
Литература.
-
Вержбицкий В.М. Основы численных методов: Учебник для вузов. – 2-е изд., перераб. – М.: Высш.шк.,2005.
-
Поршнев С.В. Вычислительная математика. Курс лекций. – СПб.:БХВ-Петербург, 2004.
-
Гусак А.А. Справочник по высшей математике. – Мн.: ТетраСистемс, 2004.
-
Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Учебное пособие для вузов/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.,2005.
-
Кетков Ю., Кетков А., Шульц М. MATLAB 7 программирование, численные методы. БХВ-Петербург, 2005.
