Лабораторное задание 2

Задание 2.

Решение трансцендентных уравнений.

Цель задания.

Практика в использовании численных методов решения трансцендентных уравнений.

Содержание задания.

1. Знакомство с численными методами решения трансцендентных уравнений.

2. Составление программы для решения трансцендентного уравнения.

3. Отладка программы и решение поставленной задачи .

Постановка задачи.

Дано: функция f(x, y), вещественные c, d и целое m (m>0). Для каждого значения 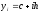(i=0,1,...m), где h=(d-c)/m, найти корень уравнения F(x)=f(x, )=0. Если уравнение имеет не единственный корень, то отдать предпочтение положительному корню, а среди корней одинакового знака предпочтение отдать наименьшему по модулю (но отличному от нуля) корню.

Каждый корень найти с точностью =0.001, используя указанные приближенные методы. Функция f(x, y), значения c, d, m и приближенный метод нахождения корня определяются вариантом задания (см. Приложение 1).

Значения c, d, m должны либо вводиться в процессе выполнения программы, либо задаваться в начале программы с помощью операторов присваивания, с тем, чтобы изменение этих значений требовало внесения минимальных изменений в программу и тем самым уменьшения возможности внесения ошибок. В качестве результатов необходимо выдать на печать таблицу значений и соответствующих им значений .

Для решения задачи следует:

1. Исследовать заданную функцию; найти отрезок, в котором находится требуемый корень уравнения при любом значении ;

проверить применимость указанного численного метода.

2. Разработать алгоритм решения поставленной задачи

3. Составить и отладить процедуру функцию вычисления F(x) (считая 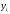глобальной величиной) и, если требуется F'(x).

4. Составить и отладить программу поставленной задачи.

Содержание отчета.

1. Постановка задачи (конкретный вариант).

2. Результаты решения задачи на ЭВМ.

Приложение 1. Варианты задания.

I. Метод приближенного решения уравнения F (x)=0.

1. Метод деления отрезка пополам.

2. Метод хорд (секущих).

3. Метод касательных (Ньютона).

4. Комбинированный метод.

II. Функция f(x, y), значения c, d, m.

N	F(x, y)	c	d	m
1		1	2	10
2		1	2	20
3		1	2	15
4		1	2	30
5		5	6	10
6		1	2	15
7				20
8		1/3	1/2	12
9		1	10	30

Приложение 2. Методические указания

1. При отладке программы следует, прежде всего, отладить описанные в ней процедуры - для этого нужно подготовить и пропустить соответствующий набор тестов.

2. Отладку численного метода решения трансцендентного уравнения целесообразно сначала провести на уравнении с заранее известным решением.

Литература.

1. Вержбицкий В.М. Основы численных методов: Учебник для вузов. – 2-е изд., перераб. – М.: Высш.шк.,2005.

2. Поршнев С.В. Вычислительная математика. Курс лекций. – СПб.:БХВ-Петербург, 2004.

3. Гусак А.А. Справочник по высшей математике. – Мн.: ТетраСистемс, 2004.

4. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Учебное пособие для вузов/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.,2005.

5. Кетков Ю., Кетков А., Шульц М. MATLAB 7 программирование, численные методы. БХВ-Петербург, 2005.