Дельта-функция Дирака

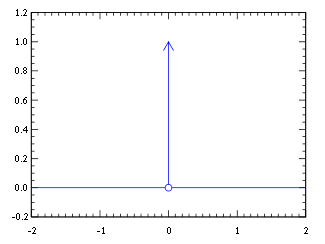
Де́льта-фу́нкция (или δ-функция, δ-функция Дирака, дираковская дельта, единичная импульсная функция)

это функция, которая в определенный момент времени равна бесконечности, а в остальное время равна 0.

Площадь под графиком этой ф-ии равна 1.

Фильтрующее свойство дельта функции

`

12. Определение базисных сигналов. Тригонометрический базис гармонических сигналов.

Сложный сигнал удобно представлять суммой простых сигналов (базисных): функцией Хевисайда, Гармоническая функция, экспоненциальный сигнал…

Гармонический сигнал можно представить в виде синуса или косинуса - это и есть базис

В линейном пространстве сигналов можно определить совокупность линейно независимых сигналов {e_i(t)} таких, что весовая сумма åa_ie_i=0 возможна только при одновременном равенстве нулю всех коэффициентов a. Эти сигналы называются координатным базисом. Базисные сигналы попарно ортогональные.

13. Обобщенный ряд Фурье. Формулы расчета весовых коэффициентов ряда Фурье. Понятие спектра сигнала.

Если выбраны сигналы координатного базиса, то любой сигнал s(t) в линейном пространстве может быть представлен взвешенной суммой ортогональных сигналов координатного базиса Сумма(С_ie_i(t)=s(t))

Такое представление сигнала называется обобщенный ряд Фурье.

Совокупность коэффициентов обобщенного ряда Фурье {Сi} называется спектром сигнала s(t) в базисе ортогональных сигналов {e_i(t)}

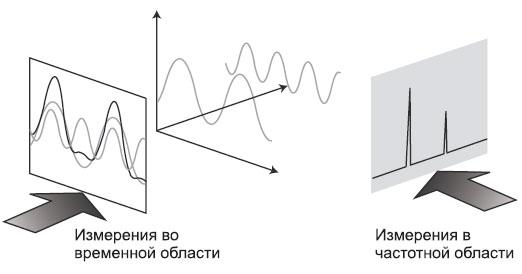
Рисунок 1-2. Связь между временной и частотной областью

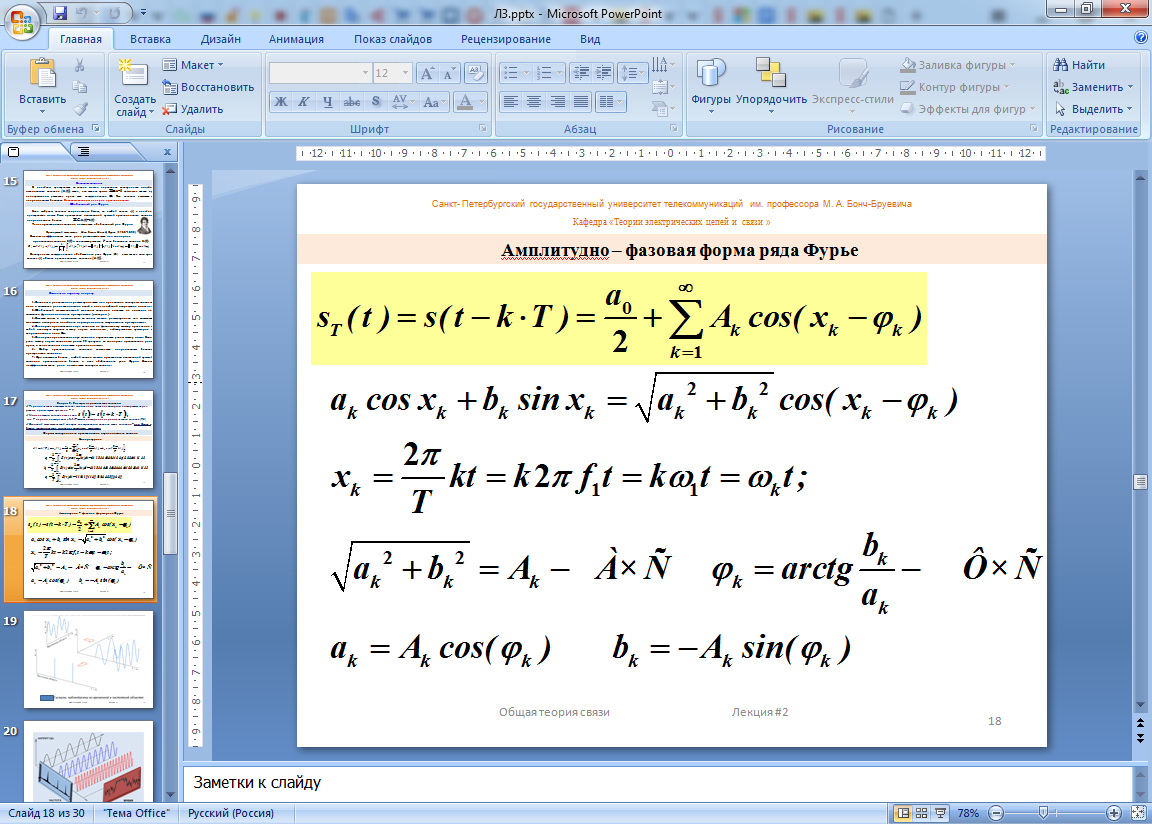
14.Периодический сигнал и формы представления его спектра в ортогональном базисе гармонических сигналов: квадратурная форма, амплитудно-фазовая форма, комплексная форма.Комплексный фазор. Понятие отрицательной частоты в гармоническом спектре.

Периодическим называют сигнал, мгновенные значения которого повторяются через равные промежутки времени – Т Модель такого сигнала имеет вид где Т- период повторения, а F=1/T-частота повторения периодического сигнала (ПС) Основной математический аппарат спектрального анализа таких сигналов –ряд Фурье в базисе гармонических сигналов с кратными частотами.

Спектр – это набор синусоидальных волн, которые, будучи надлежащим образом скомбинированы, дают изучаемый нами сигнал во временной области.

Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой. Все остальные сигналы будут негармоническими или несинусоидальными. 

15. Модель т- финитного непериодического сигнала при предельном переходе от периодического сигнала.

Моделью т финитного сигнала является периодический сигнал, у которого период повторения стремится к бесконечности

Чем больше период, тем больше частота

Следовательно гармоники в спектре будут расположены очень близко друг к другу

Поэтому мы вводим новую величину, называемую спектральной плотностью сигнала

Чтобы рассчитать спектральную плотность сигнала используют прямое преобразование Фурье

А обратное позволяет синтезировать сигнал по спектральной плотности

16. Прямое и обратное преобразование Фурье и их свойства.

17. Физический смысл спектральной плотности т-финитного сигнала. Понятие эквивалентной гармоники в спектре непериодического сигнала.

Т-финитными называют ограниченные по времени сигналы. По определению они не могут быть периодическими и, следовательно, к ним не применимо разложение в ряды Фурье.

Чтобы получить адекватное описание таких сигналов в частотной области используют следующий прием. На первом этапе от заданного сигнала x(t), имеющего начало в точке t₁ и конец в точке t₂ переходят к сигналу x_п(t), являющемуся периодическим повторением x(t) на бесконечной оси времени с периодом . Сигнал x_п(t) можно разложить в ряд Фурье

_,

где .

Введём в рассмотрение текущую частоту и спектральную плотность амплитуд .

Тогда _.

Исходный сигнал x(t) можно получить из x_п(t) в результате предельного перехода Т® ¥ .

При этом

, , å ® ò , ,

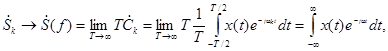
Таким образом, для описания спектра финитного сигнала приходим к известному в математике интегральному преобразованию Фурье:

– прямое,

– обратное.

В данном случае (и в дальнейшем) комплексную функцию записали в виде , как это принято в научно-технической литературе.

Из полученных соотношений следует, что спектр Т-финитного сигнала сплошной. Он представляет собой совокупность бесконечного числа спектральных составляющих с бесконечно малыми амплитудами , непрерывно следующих по оси часты. Вместо этих бесконечно малых амплитуд используют спектральную функцию (спектральную плотность амплитуд)

,

где – амплитудный спектр,

– фазовый спектр.

 

Выводы

1. Математическим аппаратом спектрального анализа Т-финитных сигналов является интегральное преобразование Фурье.

2. Спектры Т-финитных сигналов сплошные и описываются непрерывными функциями частоты в виде модуля спектральной плотности амплитуд (амплитудный спектр) и её аргумента (фазовый спектр).

18. Средняя энергия периодического сигнала. Равенство Парсеваля для вещественных сигналов.