Операторы для построения рекурсивных функций

Из уже имеющихся базисных вычислимых функций новые вычислимые функции строятся с помощью следующих операций.

Оператор суперпозиции (s) (регулярная суперпозиция)

Оператором суперпозиции S называется подстановка в функцию от m переменных m функций от n этих же переменных. Получаем новую функцию от n переменных.

С помощью оператора суперпозиции из некоторых функций:

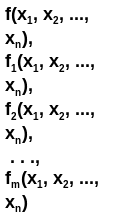
можно получить новую функцию g:

g = S^m+1(f, f₁, f₂, ..., f_m) = g(x₁, x₂, ..., x_n) =

f( f₁(x₁, x₂, ..., x_n), f₂(x₁, x₂, ..., x_n), ..., f_m(x₁, ..., x_n)).

индекс сверху m+1указывает на число функций.

Функция g является

• частичной функцией от n переменных.

• её значение определено тогда и только тогда, когда определены все выражения в правой части

• если функции f, f₁, f₂,..., f_m вычислимы, то и функция g вычислима.

Алгоритм ее вычисления описывается правой частью равенства.

Пример. При помощи оператора суперпозиции и функции выбора можно выразить любую подстановку функции в функцию.

Например, осуществляя операцию суперпозиции функций

f(x) = 0 и f₁(x) = x+1,

получим функцию:

g(x) = f₁(f(x)) = 0 + 1 = 1.

При суперпозиции функции f₁(x) с этой же функцией получим функцию

g(x) = f₁(f₁(x)) = x+1 + 1 = x+ 2.

Таким же образом с помощью оператора суперпозиции можно получить любую константу

S(S( …(Z(x)) …)) = n, где число вложенных функций следования равно n.

или сдвиг числа на константу n, также равную числу вложенных функций следования

S(S( …(S(x)) …)) = x + n

Оператор примитивной рекурсии (r)

С помощью этого оператора конструируем функцию f от n+1 переменной из некоторых частичных функций

g(x₁, x₂, ..., x_n) и

h(x₁, x₂, ..., x_n, y, z),

функция g имеет n переменных, а функция h имеет n+2 переменных.

Значения новой функции f вычисляем оператором примитивной рекурсии по двум правилам:

1. f(x₁,x₂,...,x_n,0) = g(x₁,x₂,...,x_n),

2. f(x₁,x₂,...,x_n,y+1) = h(x₁,x₂,...,x_n,y, f(x₁,x₂,...,x_n,y))

• означает вычисление значения f(x₁,x₂,...,x_n,y+1) с использованием f(x₁,x₂,...,x_n,y) (возвращением к ранее вычисленному значению).

• Приведенная пара равенств называется схемой примитивной рекурсии.

• В операции примитивной рекурсии всякую функцию от меньшего числа аргументов можно рассматривать как функцию от большего числа аргументов.

• Существенным является то, что независимо от числа переменных в f рекурсия ведется только по одной переменной у.

• Остальные n переменных x₁, x₂, ..., x_n на момент применения схемы зафиксированы и играют роль параметров.

• Большинство современных языков высокого уровня поддерживают механизм рекурсивного вызова, когда функция, как элемент структуры языка программирования, возвращающая вычисленное значение по своему имени, может вызывать сама себя с другим аргументом.

• Эта возможность позволяет напрямую реализовывать вычисление рекурсивно определенных функций.

• Любой рекурсивный алгоритм может быть реализован итерационно.

• Если программист начинает использовать оператор цикла while, в котором число итераций заранее неизвестно и может быть бесконечным, то он переходит в класс частично рекурсивных функций.