
Травень В.Ф. - Органическая химия. В 3 т. Т. 1
..pdf1.8. Природа ковалентной связи с позиций теории молекулярных орбиталей |
61 |
Еще одним важным качеством МО как волновой функции является ее
нормированность:
с12 + с22 + ... + сμ2 + ... + сn2 = 1.
В соответствии с указанными свойствами МО значение сμ2 оценивает вероятность пребывания электрона на АО χμ и называется электронной плотностью на μ-м центре.
2. Задачи теории МО решаются методами квантовой химии на основе результатов квантово-химических расчетов. При этом одним из важнейших является вопрос о базисе: какие АО следует включать в аналитическое выражение (1) для МО. Атомные орбитали, включаемые в расчет, называют базисными.
Если расчет проводят в валентном базисе, в число базисных включают все орбитали внешнего (валентного) слоя каждого атома молекулы. Для атома каждого элемента число орбиталей валентного слоя определяется максимальным значением главного квантового числа, возведенным в квадрат n2. Например, от каждого атома водорода в уравнение (1) включают только 1s-орбиталь, а от каждого атома элементов 2-го периода (в том числе углерода) — четыре орбитали: 2s, 2px, 2py, 2pz. Таким образом, при расчете молекулы метана в валентном базисе
аналитическое выражение (1) для молекулярной орбитали принимает вид: |
|
ϕ = с1χ(2s) + с2χ(2px) + с3χ(2py) + с4χ(2pz) + с5χ(1s) + с6χ(1s) + |
|
+ с7χ(1s) + с8χ(1s). |
(2) |
Соответственно при расчете молекулы этилена в валентный базис должны быть включены 12 АО.
Если расчет проводят в π-базисе, от каждого атома элемента 2-го периода в выражение (1) для ϕ включают только одну 2pz-орбиталь. При расчете молекулы этилена, например, в π-базис должны быть включены только две АО — 2pz-орбитали двух атомов углерода.
Число АО, включаемых в число базисных (размер базиса), определяет число МО, получаемых в результате расчета. Таким образом, при расчете молекулы этилена в валентном базисе имеем двенадцать МО, а при расчете в π- базисе — две МО. При этом каждая МО ϕi, получаемая при расчете, характеризуется набором собственных коэффициентов [сn]i и собственной энергией εi.
3. Чтобы найти набор собственных коэффициентов [сn]i и собственную энергию εi каждой i-й МО, нужно на волновую функцию (1) подействовать
оператором энергии Н (гамильтониан) в соответствии с уравнением Шрёдингера
H ϕ = εi ϕi |
(i = 1, 2, ..., n). |
(3) |
Действие оператора энергии Н на волновую функцию ϕ позволяет оценить кинетическую и потенциальную энергию электрона (Н = Т + V ). Этот оператор энергии применяют в простых квантово-химических расчетах.
Уравнение Шрёдингера имеет точное решение лишь для наиболее простых объектов, например, атома водорода. В результате этого решения математически точно определены все возможные состояния электрона в атоме водорода.

62 Глава 1. Природа ковалентной связи. Электронные эффекты. Кислоты и основания
Для молекул возможно лишь приближенное решение уравнения Шрёдингера. В квантовохимических расчетах молекул вместо оператора Н в уравнении Шрёдингера применяют оператор F (фокиан*); его действие на волновую функцию позволяет оценить еще и энергию межэлектронного взаимодействия (F = Т + V + E). Этот оператор энергии используют в расчетах молекул по методу самосогласованного поля (ССП).
В общем виде алгоритм решения квантово-химической задачи заключается в следующем.
Умножают обе части уравнения Шрёдингера (3) на ϕ, интегрируют полученное выражение и получают выражение энергии в интегральной форме.
ϕHϕ = εϕ2, ε = ∫ϕHϕdτ / ∫ϕ2dτ.
Подставляют вместо ϕ его аналитическое выражение
∫(c1χ1 |
+ c2χ2 |
+ ... + cnχn)H(c1χ1 + c2χ2 + ... + cnχn) dτ |
(4) |
|||
ε = . |
||||||
|
|
∫(c |
χ |
+ c χ |
+ ... + c χ )2dτ |
|
|
|
1 |
1 |
2 2 |
n n |
|
Для нахождения минимальных значений собственной энергии применяют вариационный метод: последовательно дифференцируют полученное выражение (4) для энергии по коэффициентам с1, с2, ..., сn и приравнивают полученные значения первых производных нулю.
Указанная процедура сводит квантово-химическую задачу к математической задаче — решению системы уравнений, линейных относительно коэффициентов (система уравнений Рутаана). В рамках простых методов эта система имеет вид:
n |
|
∑ (Hμν – εi Sμν)сiμ = 0, |
(5) |
μ = 1
где i = 1, 2, ..., n; Hμν — элементы оператора энергии, оценивающие энергию электрона в области перекрывания атомных орбиталей χμ и χν; Sμν — интегралы перекрывания, оценивающие область перекрывания атомных
орбиталей χμ и χν.
Результатом решения системы уравнений (5) является получение n наборов собственных коэффициентов [сn]i и n значений собственной энергии εi для n молекулярных орбиталей ϕi:
ϕi = ci1χ1 + ci2χ2 + … + ciμχμ + cinχn.
Здесь i — индекс МО (i = 1, 2, …, n), μ — индекс АО (μ = 1, 2, …, n).
* Названия операторов энергии были введены по фамилиям ученых, предложивших соответствующие приближения для решения уравнения Шрёдингера. В частности, фокиан был предложен в 1930 г. нашим соотечественником академиком В.А. Фоком.

1.8. Природа ковалентной связи с позиций теории молекулярных орбиталей |
63 |
4.Молекулярные орбитали подчиняются тем же правилам заполнения электронами, что и атомные орбитали. Для них возможны числа заполне-
ния gi, равные 0, 1 или 2. Соответственно этим числам на молекулярной орбитали могут находиться один или два электрона; такие МО называют занятыми. Молекулярная орбиталь может не содержать ни одного электрона; такие МО называют свободными.
5.Заполнение молекулярных орбиталей электронами начинается с ϕ1, имеющей самое низкое значение собственной энергии ε1.
Таким образом, в результате расчета молекулы метана в валентном базисе получают восемь МО. Размещая на них восемь валентных электронов, по-
лучают четыре занятые МО (ϕ1, ϕ2, ϕ3, ϕ4) и четыре свободные МО (ϕ5, ϕ6, ϕ7, ϕ8). Орбиталь ϕ4 называют высшей занятой молекулярной орбиталью (ВЗМО), а орбиталь ϕ5 — низшей свободной молекулярной орбиталью (НСМО).
ВЗМО и НСМО являются граничными молекулярными орбиталями.
 ОБРАТИТЕ ВНИМАНИЕ!
ОБРАТИТЕ ВНИМАНИЕ!
Высшая занятая молекулярная орбиталь (ВЗМО) — занятая электронами
молекулярная орбиталь, обладающая наиболее высокой энергией.
Низшая свободная молекулярная орбиталь (НСМО) — свободная (не занятая
электронами) молекулярная орбиталь, обладающая самой низкой энергией. Занятые МО, имеющие энергию меньше, чем исходные АО, называют связывающими. Свободные МО, имеющие энергию выше, чем исходные АО, называют разрыхляющими; при попадании электронов на них система де-
стабилизируется.
1.8.2. Простой метод Хюккеля (метод МОХ)
Водном из простых квантово-химических методов — методе Хюккеля (метод МОХ) — расчеты параметров электронной структуры органических молекул проводят при следующих приближениях.
1. Расчеты проводят в π-базисе. От каждого атома элемента 2-го периода
врасчет вводят только по одной орбитали — 2рz-орбитали.
2.При решении системы уравнений Рутаана (5) интегралы Нμμ для атома углерода приравнивают к α и называют кулоновским интегралом. Этот интеграл оценивает энергию электрона в поле атома углерода.
3.Интегралы Нμν, оценивающие энергию электрона в поле двух атомов, для соседних атомов углерода приравнивают к β и называют резонансным интегралом. Для несоседних атомов этот интеграл приравнивают нулю.
4.Интегралы Sμν, оценивающие перекрывание μ-й и ν-й орбиталей, называют интегралами перекрывания. Эти интегралы приравнивают к единице при μ = ν и приравнивают к нулю при μ ≠ ν.

64Глава 1. Природа ковалентной связи. Электронные эффекты. Кислоты и основания
5.В методе МОХ могут быть рассчитаны лишь плоские молекулы, имеющие сопряженные системы связей, в том числе содержащие гетероатомы. Для гетероатомов в значения параметров α и β вводят поправки и принимают следующие числа заполнения m атомных орбиталей электронами.
Атом |
С |
N |
N |
О |
О |
Cl |
|
|
(sp3, анилин) |
(sp2, пиридин) (sp3, фенол) (sp2, карбонил) |
|
||
m |
1 |
2 |
1 |
2 |
1 |
2 |
Несмотря на значительное число приближений, принятых в методе МОХ, результаты расчета этим методом показывают плодотворность кван- тово-химического подхода в получении объективных оценок распределения электронных плотностей, в том числе и в достаточно сложных органических молекулах. Ниже рассмотрен ряд примеров расчетов по методу МОХ.
Расчет молекулы этилена
Процедура расчета включает следующие операции.
1. Нумеруют орбитали, включаемые в базис. Это 2рz-орбитали двух атомов углерода:
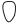 1
1  2
2
2. Записывают систему уравнений (5): |
|
||
(H11 – ε S11)с1 + (H12 – ε S12) с2 = 0 |
(6) |
||
{(H21 – ε S21)с1 + (H22 – ε S22) с2 = 0 |
|
||
3. Вводят принятые в методе МОХ обозначения |
|
||
H11 = H22 = α; H12 = H21 = β; S11 = S22 = 1; S12 = S21 = 0 |
|
||
в систему (6) |
|
||
(α – ε)с1 |
+ βс2 = 0 |
(7) |
|
{βс1 + (α |
– ε)с2 = 0 |
||
|
|||
4. Система уравнений (7) имеет ненулевое решение, если соответствующий ей вековой определитель, составленный из коэффициентов при с1 и с2, равен нулю.
| (α –β ε) (α –β ε)| = 0 |
(8) |

1.8. Природа ковалентной связи с позиций теории молекулярных орбиталей |
65 |
Разделив все члены этого определителя на β и заменив (α – ε)/β = х, получают
|1х |
х1 |= 0, |
откуда при х1, 2 = ±1 собственные значения указанной выше системы равны:
ε1 = α + β, ε2 = α – β.
5. Найденные значения ε1 и ε2 представляют собой собственные энергии молекулярных π-орбиталей ϕ1 и ϕ2 этилена. Чтобы найти собственные коэффициенты этих МО, последовательно подставляют значения ε1 и ε2 в уравнения (7). Например, при ε1 = α + β получают
{–βc1 + βc2 = 0 βc1 – βc2 = 0,
откуда следует, что с1 = с2. |
= 1, выражение для ϕ |
|
этилена приобретает вид: |
||
При условии, что с2 + с2 |
1 |
||||
|
1 |
2 |
|
|
|
|
|
χ2 = 0,707χ1 + 0,707χ2. |
|
|
|
ϕ1 = 1/√ 2 |
χ1 + 1/√ 2 |
|
|
||
Аналогично при ε2 = α – β получают выражение для ϕ2 этилена: ϕ2 = 0,707χ1 – 0,707χ2.
Электроны размещают на МО попарно, начиная с ϕ1, имеющей самое низкое значение энергии. Эта орбиталь в этилене является занятой. При расчете в π-базисе ϕ1 оказывается и высшей занятой молекулярной орбиталью (ВЗМО). Орбиталь ϕ2 является свободной, а в данном примере — низшей свободной молекулярной орбиталью (НСМО) этилена.
ε2 |
|
|
|
|
|
|
ϕ2 |
НСМО (разрыхляющая) |
|
|
|
|
|
|
|
||||
α |
|
|
|
|
|
|
|
ВЗМО (связывающая) |
|
|
|
|
|
|
|
|
|||
ε1 |
|
|
|
|
|
|
ϕ1 |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Энергия π-электронов молекулы этилена оказывается равной
Eπ = 2ε1 = 2(α + β).
Размещение электронов на орбитали ϕ1 стабилизирует систему. По сравнению с энергией электронов двух изолированных атомов углерода (2α) выигрыш энергии Eπ составляет
Eπ = 2(α + β) – 2α = 2β.

66 Глава 1. Природа ковалентной связи. Электронные эффекты. Кислоты и основания
Расчет молекулы 1,3-бутадиена
Аналогично в рамках метода МО рассчитывают молекулу 1,3-бутадиена. В табл. 1.9 приведены результаты этого расчета: собственные энергии и собственные коэффициенты МО расположены по строкам снизу вверх в порядке возрастания энергии начиная с ϕ1, а собственные коэффициенты соответствующих МО, относящиеся к отдельным атомам, даны в столбцах.
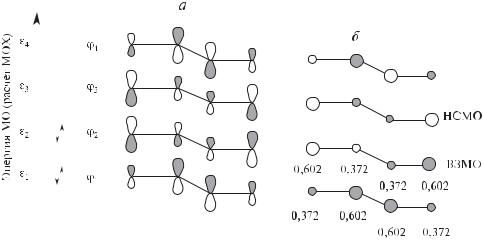
Энергетическая диаграмма и графические изображения МО 1,3-бутади- ена представлены на рис. 1.6 (размеры «гантелек» и кружков пропорциональны значениям собственных коэффициентов; положительные доли орбиталей затемнены).
Собственные коэффициенты МО позволяют рассчитывать ряд параметров электронной структуры молекулы.
1. Электронная плотность ρμ на атоме.
Электронная плотность на μ-м атоме в i-й МО обозначается ρiμ:
ρiμ = gi сiμ2.
Значения ρ на отдельных атомах в ВЗМО 1,3-бутадиена показаны ниже.
ρ(ВЗМО) 1 = 2 (–0,602)2 = 0,72
|
|
|
ВЗМО |
0,72 |
0,28 |
0,28 |
0,72 |
Всумме на ВЗМО находятся два электрона (0,72 + 0,28 + 0,28 + 0,72 = 2,00). Полная электронная плотность на μ-м атоме определяется суммирова-
нием значений электронной плотности на μ-м атоме по всем занятым МО:
зан
ρμ = ∑ gi сiμ2, i = 1
ρ1 = 2(0,372)2 + 2(–0,602)2 = 1,000.
Таблица 1.9. Результаты расчета МО молекулы 1,3-бутадиена
|
|
|
|
|
Номер |
Энергия |
Собственные коэффициенты* МО |
|||
1 |
|
2 |
|
|
МО |
МО |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
||
CH2 |
|
CH 3 |
4 |
4 |
α – 1,618 β |
–0,372 |
0,602 |
–0,602 |
0,372 |
|
|
||||||||||
|
||||||||||
|
|
CH |
|
CH2 |
3 |
α – 0,618 β |
–0,602 |
0,372 |
0,372 |
–0,602 |
|
|
|
||||||||
|
|
|
||||||||
|
|
|
|
|
2 |
α + 0,618 β |
–0,602 |
–0,372 |
0,372 |
0,602 |
|
|
|
|
|
1 |
α + 1,618 β |
0,372 |
0,602 |
0,602 |
0,372 |
|
|
|
|
|
|
|
|
|
|
|
* 1–4 — номера АО (в методе МОХ — номера атомов).
1.8. Природа ковалентной связи с позиций теории молекулярных орбиталей |
67 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.6. Энергетическая диаграмма и графические изображения молекулярных π-орбиталей 1,3-бутадиена: а — вид спереди, б — вид сверху
2.Заряд на атоме Zμ определяют по разности Zμ = mμ – ρμ, Z1 = 1 – 1,000 = 0.
3.Порядки π-связей между атомами.
Порядок между μ-й и ν-й АО в i-й МО называют дробным порядком связи и находят по формуле
(pμν)i = gi сiμ сiν.
Полный порядок π-связи между μ-м и ν-м атомами определяется суммированием порядков по всем занятым МО:
зан
Pμν = ∑ gi сiμ сiν. i = 1
Проделав указанные выше расчеты, получаем следующие порядки связей для молекулы 1,3-бутадиена:
1,896 1,448 1,896
CH2

 CH
CH

 CH
CH

 CH2 .
CH2 .

68 Глава 1. Природа ковалентной связи. Электронные эффекты. Кислоты и основания
4. Особый интерес представляет оценка энергии делокализации
π-электронов Eπ (делок) на основе расчета методом МОХ. Для этого значение энергии π-электронов молекулы
зан
Еπ = ∑ gi εi i = 1
cравнивают с энергией, рассчитанной из условия локализации двойных связей
Еπ (лок) = n • 2 (α + β),
где n — число двойных связей в молекуле.
Для 1,3-бутадиена значение π-электронной энергии
Еπ = 2(α + 0,618β) + 2(α + 1,618β) = 4α + 4,472β
сравнивают со значением энергии π-электронов Еπ (лок), рассчитанным из условия их локализации в двух двойных связях.
Еπ (лок) = 2(α + β) + 2(α + β) = 4α + 4β.
Разность полученных значений энергий является мерой эффекта сопряжения π-связей в молекуле 1,3-бутадиена:
Еπ (делок) = Еπ – Еπ (лок) = 0,472β.
Ниже в качестве примера оценена энергия делокализации Eπ (делок) в молекуле бензола.
Еπ = 2ε1 + 2ε2 + 2ε3 = 2(α + 2β) + 4(α + β) = 6α + 8β, Еπ (лок) = 3[2(α + β)] = 6α + 6β, Еπ (делок) = 6α + 8β – (6α + 6β) = 2β.
Сравнивая полученное из расчета значение энергии делокализации 2β с экспериментальным значением энергии делокализации в молекуле бензола, равным 150,6 кДж/моль (36 ккал/моль), можно оценить численное значение резонансного интеграла β:
2β = 150,6 кДж/моль (36 ккал/моль), β = 75 кДж/моль (18 ккал/моль).
В этом разделе были рассмотрены примеры расчетов электронного строения органических молекул в рамках наиболее доступного метода квантовой химии — простого метода Хюккеля (метод МОХ). Учитывая приближенность этого метода, результаты, получаемые на его основе, следует применять лишь для сравнительных оценок тех или иных свойств органических соединений. Тем не менее нужно иметь в виду, что возможности современных вычислительных методов квантовой химии практически неограничены. Для органических молекул любой сложности в настоящее
1.9. Классификация органических реакций |
69 |
время доступны расчеты значений электронной плотности, зарядов на атомах и порядков связей, сравнимые по точности с результатами самых совершенных физических измерений.
1.9.КЛАССИФИКАЦИЯ ОРГАНИЧЕСКИХ РЕАКЦИЙ
Известно огромное число различных превращений органических соединений, с помощью которых химики могут получать практически любые вещества заданного строения. Ориентироваться во множестве органических реакций помогает их классификация. В этом разделе излагается основа классификации превращений органических веществ.
Органические реакции классифицируют по различным признакам:
—по типу превращения субстрата;
—по типу активирования;
—по характеру разрыва связей.
Особую группу органических реакций составляют одноэлектронные реакции.
1.9.1.Классификация по типу превращения субстрата
Реакции замещения
Замещение — реакция, в ходе которой атом водорода (или функциональная группа) в органической молекуле замещается на какую-либо функциональную группу (или атом водорода). В общем виде реакцию замещения X  Y можно записать в виде:
Y можно записать в виде:
R–X + Y |
|
R–Y + X |
(1) |
|
реагенты продукты
Исходные соединения в органических реакциях называют реагентами, а образующиеся соединения — продуктами. В уравнении (1) R–X и Y — реагенты, а R–Y и X — продукты.
Для удобства один из реагентов принято называть субстратом, а другой — атакующим реагентом. Как правило, субстрат имеет более сложное строение, атакующий реагент часто имеет неорганическую природу. Например, в реакции метана с хлором
CH4 |
+ Cl2 |
hν, t |
CH3Cl |
+ |
HCl |
(2) |
|
||||||
метан |
хлор |
|
хлорметан |
|
хлороводород |
|
(субстрат) |
(реагент) |
|
(продукт) |
(побочный продукт) |
|
|
метан является субстратом, а хлор — атакующим реагентом.
70 Глава 1. Природа ковалентной связи. Электронные эффекты. Кислоты и основания
Символами над стрелкой обозначают условия, требуемые для проведения реакции; в реакции (2) такие условия — УФ-облучение и нагревание.
Реакции замещения обозначают латинской буквой S (от англ. “substitution” — замещение).
Реакции замещения атома водорода часто называют по вступающей функциональной группе. Реакцию (2) называют, например, реакцией хлорирования (H  Cl, т. е. атом водорода замещается на атом хлора).
Cl, т. е. атом водорода замещается на атом хлора).
Другим примером реакции замещения водорода можно назвать нитрование бензола (H  NO2):
NO2):
|
|
|
|
|
NO2 |
(3) |
|
|
|
|
|
|
|
|
|
+ NO2BF4 |
|
|
|
+ HBF4 |
бензол |
нитроний- |
нитробензол |
тетрaфторборо- |
|||
(субстрат) |
тетрафторборат |
(основной |
водородная кислота |
|||
|
|
(реагент) |
продукт) |
(побочный продукт) |
||
Замещению могут подвергаться не только атомы водорода, но и различные функциональные группы, ранее введенные в молекулы углеводородов. Например, замещение Cl  OH:
OH:
CH3Cl + |
OH |
|
CH3OH + Cl |
(4) |
|
||||
хлорметан |
гидроксид- |
метанол хлорид- |
|
|
|
ион |
ион |
|
|
Группу Х в субстрате R–X [реакция (1)] принято называть уходящей группой, а группу Y — вступающей группой; в реакции (4) Cl — уходящая группа, ОН — вступающая группа.
Реакции присоединения
Присоединение — реакция, в ходе которой реагент присоединяется по кратной связи (С=С, С=О, С=N) молекулы субстрата. Это, например, гидробромирование этилена:
СН2=СН2 |
+ HBr |
|
CH3CH2Br |
(5) |
|
||||
этилен |
бромоводород |
|
бромэтан |
|
Реакции присоединения обозначают латинским символом Аd (от англ. “addition” — присоединение). Продукт такой реакции обычно называют аддуктом. Другие примеры реакций присоединения:
— образование циангидрина ацетальдегида
|
|
|
O |
|
|
|
|
|
OH |
|
|||
CH3 |
|
C |
+ HCN |
|
|
|
CH3 |
|
|
|
|
|
(6) |
|
|
|
|
|
C |
|
CN |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
ацетальдегид |
циановодород |
циангидрин |
|
|
ацетальдегида |
|
|
(аддукт) |
