Задача 5. Расчет производительности строительных процессов с учетом надежности рабочих и техники
Исходные данные:
- вероятность безотказной работы техники Рт = 0,80;
- вероятность безотказной работы людей Рч = 0,90;
- рассматриваемый интервал времени для техники Тсм = 200 смен;
- рассматриваемый интервал времени для людей Тдн = 100 дней;
- продолжительность восстановления для техники tвт = 3 смены;
- продолжительность восстановления для людей tвч = 3 дня;
- продолжительность отказа для техники tот = 3 смены;
- продолжительность отказа для людей tоч = 3 дня.
Работа выполняется комплектом машин в составе:
- экскаватор «прямая лопата»;
- 5 автосамосвалов;
- бульдозер;
- уплотняющая машина.
Решение:
Вероятность отказа каждой машины: qt = 1 – Pт = 1 – 0,8 = 0,2. На указанном интервале времени Тсм в 200 смен это составит 200*0,2 = 40 смен.
Число отказов техники на исследуемом промежутке времени:
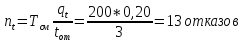
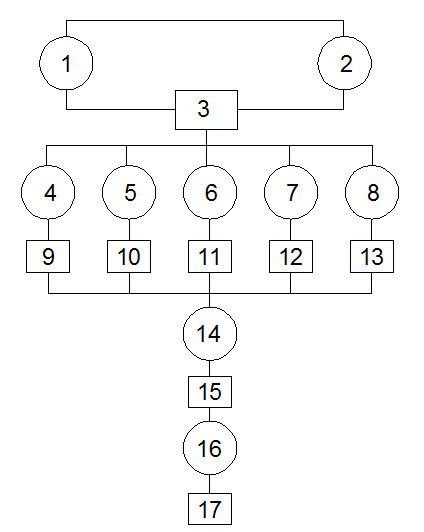
Графическая модель процесса производства земляных работ экскаваторным комплектом
Интенсивность отказов техники на исследуемом промежутке времени:
λt = nt / Tсм = 13/200 = 0,065
Интенсивность восстановления техники:
μt = 1/tвт = 1/3 = 0,33
Вероятность отказа рабочих:
qч = 1 – Pч = 1 – 0,9 = 0,1. На указанном интервале времени Тдн в 100 дней это составит 100*0,1 = 10 дней.
Число отказов рабочих на исследуемом промежутке времени:
nч = Тдн/Точ = 100*0,10/3 = 3 отказа
Интенсивность отказов рабочих на исследуемом промежутке времени:
λч= nч / Tдн = 3/100 = 0,03
Интенсивность восстановления рабочих:
μч = 1/tвч = 1/3 = 0,33
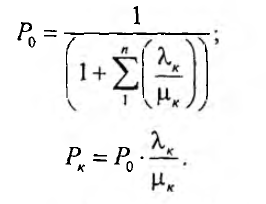
Для удобства расчет сведем в таблицу. Сначала найдем производительность производящей системы (элементы с 1 по 3 включительно). Результаты представлены в таблице 12.
Затем найдем производительность обслуживающей системы (элементы с 4 по 17 включительно). Результаты представлены в таблице 13.
Таблица 12
|
К |
Рк |
Фк |
|
0 |
0,725 |
1,00 |
|
1 |
0,066 |
0,50 |
|
2 |
0,066 |
0,50 |
|
3 |
0,143 |
0,00 |
|
∑ |
1,000 |
|
W1 = 0,725*1,00 + 0,066*0,5 + 0,066*0,5 + 0,143*0 = 0,791
Таблица 12
|
К |
Рк |
Фк |
|
0 |
0,367 |
1,00 |
|
4 |
0,033 |
0,80 |
|
5 |
0,033 |
0,80 |
|
6 |
0,033 |
0,80 |
|
7 |
0,033 |
0,80 |
|
8 |
0,033 |
0,80 |
|
9 |
0,072 |
0,80 |
|
10 |
0,072 |
0,80 |
|
11 |
0,072 |
0,80 |
|
12 |
0,072 |
0,80 |
|
13 |
0,072 |
0,80 |
|
14 |
0,033 |
0,00 |
|
15 |
0,072 |
0,00 |
|
16 |
0,033 |
0,00 |
|
17 |
0,072 |
0,00 |
|
∑ |
1,100 |
|
W2 = 0,367*1,0 + 5*0,8*0,033 + 5*0,8*0,072 = 0,787
Ф = W1*W2 = 0,791*0,787 = 0,62 => 62% - вероятность безотказной работы системы.
Вывод: благодаря наличию последовательно-параллельных связей строительная система обладает невысокой надежностью. Даже если в ней задействованы элементы, имеющие максимальную вероятность безотказной работы, вероятность безотказной работы всей системы будет всего 62%. Поэтому при расчете производительности строительных процессов необходимо учитывать надежность их элементов.