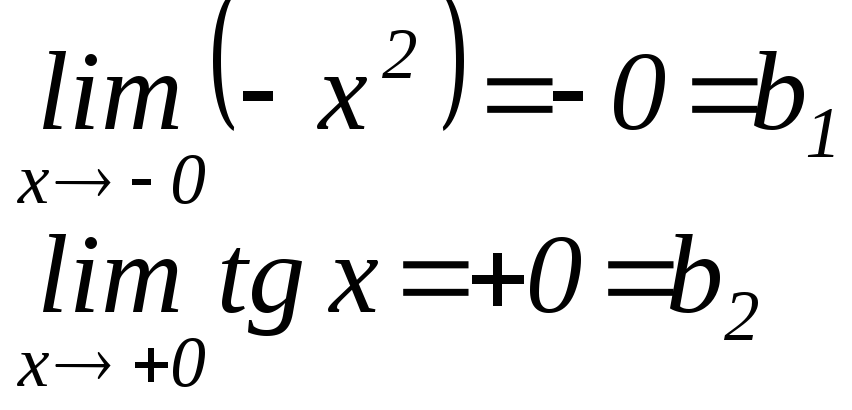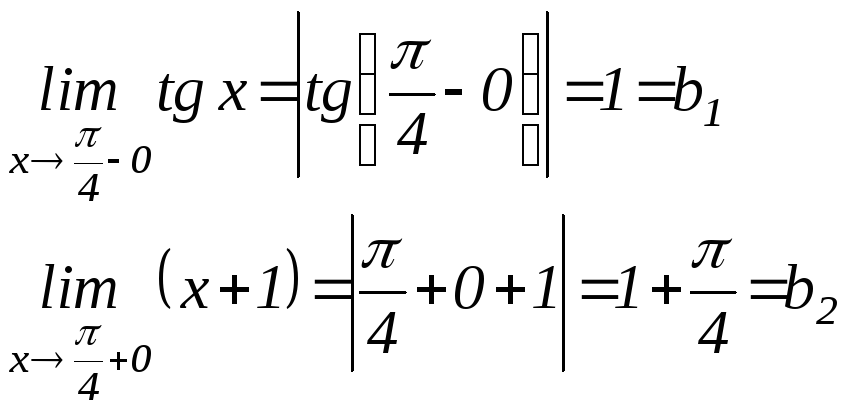Вычисление пределов, сводящихся ко второму замечательному пределу.

Как определить, что предел сводится к виду второго замечательного предела? Такие пределы всегда имеют неопределенное выражение вида . Чтобы проверить, существует ли такая неопределенность, как и во всех предыдущих примерах, предельное значение переменной подставляют в функцию. Здесь мы столкнемся с использованием техники вычисления пределов из-го раздела, где выделялась главная часть числителя и знаменателя рациональной дроби. В связи с этим напомним, что главной частью многочлена

при является слагаемое в наибольшей степени,

а при - в наименьшей степени (причем свободный член отсутствует)..

Например: ,здесь выделена главная часть числителя и знаменателя рациональной дроби, очевидно, что показатель степени стремится к бесконечности, и в конечном счете этот предел не имеет неопределенного выражения.

Если же - такой предел сводится к виду второго замечательного предела:

; или .

Анализ выражения, стоящего под знаком второго замечательного предела, показывает, что его конструкция такова - к единице прибавляется бесконечно малая величина , и эта сумма возводится в степень, равную обратной величине прибавляемой бесконечно малой, т.е. или. Если в таком примере к основанию степени прибавить и отнять единицу, то выражение не изменится, но мы сможем определить вид прибавляемой бесконечно малой величины.

, ПРИМЕРЫ

	Прибавим и вычтем единицу в основании данной функции (выражение в скобках), таким образом, она будет выделена.
=	Два последних слагаемых приведем к общему знаменателю.
= = =		Очевидно, величина , т.е. является БМ. Выделим главные части многочленов при:. Теперь предел приведен к виду второго замечательного предела, в котором. 

 =		Выделим единицу в основании и используем эквивалентность БМ величин.
==
===	Можно ввести новую переменную, чтобы показать, что предел приведен к виду второго замечательного предела. Здесь . 

Задание 2. Исследовать функции на непрерывность и классифицировать точки разрыва.

 

 Пример



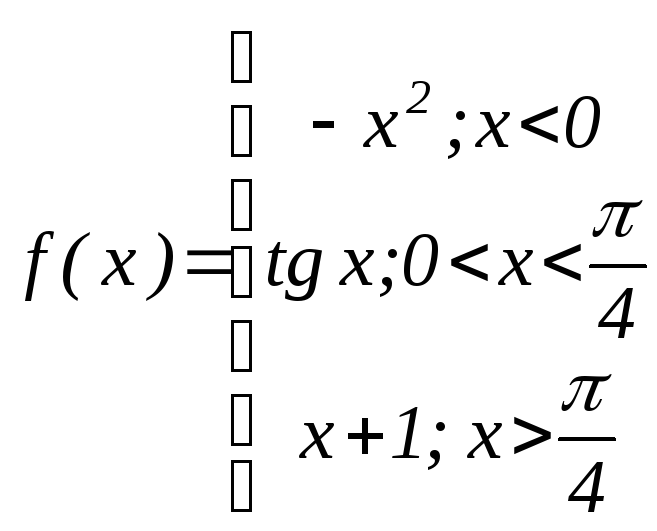
Функция f(x) , заданая условно-функциональным соотношением, определена на всей числовой оси, а функции, ее составляющие, непрерывны на заданных интервалах. Но в точках х=0 и изменяется аналитическое задание функции. Поэтому точких=0 и - возможные точки разрыва.

Исследуем на разрыв точку х=0.

b1=b2; односторонние пределы в этой точке конечны и равны между собой.

В т. х₀ разрыв 1-го рода, устранимый. Устранить разрыв можно, доопределив функцию в точке разрыва. Пусть у(0)=0, тогда в т. х₀=0 функция будет непрерывной.

Исследуем на разрыв точку

b1b2; односторонние пределы конечны, но не равны между собой.

В т. существует разрыв 1-го рода, конечный скачок. Величина скачка

 

 Пример



Преобразуем знаменатель функции в произведение, определив корни квадратного трехчлена.

Тогда Функция не определена в точкахх=3 и х=-1.

Исследуем на разрыв точку х=3.

Можно сделать вывод, что в точке х=3 имеется разрыв 2-го рода.

Исследуем на разрыв точку х=-1.

В т. х=-1 также имеется разрыв 2-го рода.



 

 ПРИМЕР



Заданная функция непрерывна на всей числовой оси, кроме точки х=-1. Исследуем функцию на разрыв в этой точке.

Так как левосторонний предел функции бесконечен, то в точке х=-1 разрыв 2-го рода. 

Задание 3. Сумма первоначального вклада составляет А денежных единиц. Процентная ставка q процентов годовых. 1) Найти наращенное значение вклада на конец n-го года отдельно для вклада под простые проценты и под сложные. 2) Найти наращенное значение вклада при ежеквартальном, ежемесячном и непрерывном начислениях сложных процентов в конце n-го года. Сравнить результаты, сделать вывод. 3) По основной формуле начисления сложных процентов и по формуле непрерывного начисления процентов рассчитать :

• за сколько лет произойдет увеличение первоначального вклада в 1.5 раза;

• какой должна быть годовая процентная ставка, чтобы за n лет вклад увеличился в 1.5 раза;

• сумму первоначального вклада (дисконтированную сумму), которую необходимо вложить для получения в конце n-го года в 1.5 большей суммы.

 
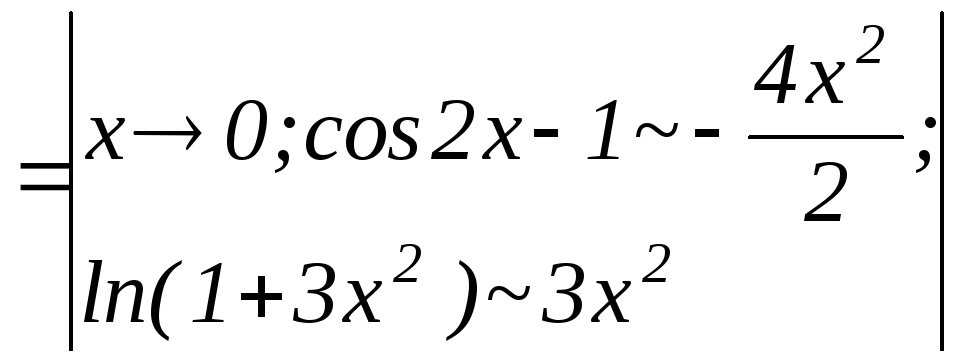