Тема 4. Теория Элементы математического анализа. Функция одной переменной

• Переменная у называется функцией переменной х, если каждому значению переменной х из некоторой области соответствует одно или несколько значений переменной у.

В настоящем разделе используются общепринятые обозначения (если не оговаривается что-либо иное):

х – независимая переменная или аргумент функции;

у – переменная, зависящая от х, или функция.

Функциональная зависимость y=f(x) или, что то же самое у=у(х), может быть изображена графиком функции в координатах (х,у).

Графики и основные свойства элементарных функций приведены в приложении.

Тема 4: Предел и непрерывность функции. Техника вычисления пределов. Классификация разрывов функции Понятие предела функции в точке. Односторонние пределы функции в точке

Понятие предела функции в точке связано с особенностями вычисления значений функции в некоторых точках, когда при подстановке значения х=а получаем неопределенное, неоднозначное выражение для вычисления у. Например: ;

; .

В таких случаях требуется проанализировать поведение функции вблизи точки х=а , и этот анализ основан на ряде понятий, которые вводятся в данной теме.

Любой интервал(; ), содержащий точку х, т.е. <x<, называется окрестностью точки х. Если выбрать любое положительное число , то -окрестностью (дельта-окрестностью) называется интервал (х-; х+). -окрестность симметрична относительно точки х, чего может и не быть в случае произвольной окрестности.

Неравенство илиозначает, что точка, т.е. принадлежит-окрестности точки а.

А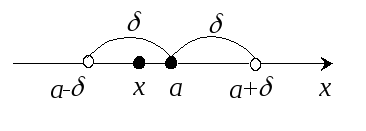налогично можно выбрать-окрестность (эпсилон-окрестность) для значения функции, равного b.

Тогда принадлежность произвольной точки у -окрестности точки b можно записать в виде:

Теперь дадим определение предела функции в точке основываясь на понятии окрестности точки на языке "-".

Пусть функция у=у(х) определена в некоторой окрестности точки х=а. В самой точке х=а функция может быть и не определена.

 Число b называется пределом функции y=y(x) при xa (х стремящемся к а) если для любого сколь угодно малого положительного числа >0 можно найти такое число  >0, зависящее от , что для всех х, удовлетворяющих неравенству справедливо неравенство.

Выражение "х стремится к а" означает, что независимая переменная х принимает значения, все более близкие к значению х=а. В общем случае они могут быть расположены как слева, так и справа от х=а. Например, пусть x_i тем ближе к а, чем больше номер i (i=1,2,3)

Приведем геометрическую интерпретацию определения предела функции в точке, для функции, определенной в точке а.

Из рисунка видно, что при произвольном выборе -окрестности точки b, можно найти симметричную -окрестность точки а (для этого надо выбрать , такую, что для любого значения переменнойх, попадающей в -окрестность точки а, соответствующее значение функции y(x) будет попадать в -окрестность точки b. Именно об этом говорится в определении предела на языке неравенств.

Факт существования предела функции, равного числу b при ха записывается:

При определении предела не уточнялось, каким образом х стремится к а, поэтому введем односторонние пределы функции в точке или пределы слева и справа.

Если независимая переменная х принимает значения, все более близкие к а, но остается при этом меньше а (слева от а), то можно получить левосторонний предел функции или предел слева:

 Число b₁ (b₂) называется пределом функции слева (справа) при ха-0 ( ха+0) если для любого, сколь угодно малого числа  >0 можно найти такое число ( ) >0, что для всех х, удовлетворяющих неравенству а-<x<a (а<x<a+) справедливо неравенство:

.

Обозначим:

Заметим, что если независимая переменная х может стремиться к числу а слева или справа, функция y может стремиться к значению b сверху или снизу.

Например, функция, представленная на рисунке (стр. 6.), стремится к значению b сверху, если ха+0 (справа) и снизу, если ха-0 (слева). Записывается это так: