
А. П. ПОТАПОВ
Математический анализ, часть 1
Теория, задачи и упражнения
Учебное пособие
Оглавление
I. Теория.
Раздел 1. Дифференциальное исчисление функций одной переменной
Глава 1. Производная и дифференциал |
… 2 |
||
Глава 2. Основные теоремы дифференциального исчисления |
… |
27 |
|
Глава 3. |
Исследование функций |
… |
53 |
Раздел 2. Интегральное исчисление функций одной переменной |
|
|
|
Глава 4. |
Неопределенный интеграл |
… |
85 |
Глава 5. |
Определенный интеграл |
… |
119 |
Глава 6. Приложения определенного интеграла |
… |
142 |
|
Глава 7. |
Несобственные интегралы |
… |
172 |
II. Задачи и упражнения. |
|
|
|
Задачи к главе 1 |
… |
201 |
|
Задачи к главе 2 |
… |
205 |
|
Задачи к главе 3 |
… |
207 |
|
Задачи к главе 4 |
… |
210 |
|
Задачи к главе 5 |
… |
213 |
|
Задачи к главе 6 |
… |
215 |
|
Задачи к главе 7 |
… |
217 |
|
Ответы |
|
… |
219 |
Литература |
|
… |
231 |
2
I. Теория.
Раздел 1. Дифференциальное исчисление функций одной переменной
Глава 1. Производная и дифференциал
Содержание
§ 1. |
Производная функции …………………………………………………………………… 3 |
|
§ 2. |
Производные основных элементарных функций ………………..……… 9 |
|
§ 3. |
Понятие дифференцируемости |
.....………………………………………… 11 |
§4. Правила вычисления производных……………………………………….………. 13
§5. Специальные методы дифференцирования функций …………………… 19
§6. Дифференциал функции …………………………….…………………………………… 21

3
§ 1. Производная функции.
Дана функция |
|
с областью определения |
. Пусть |
внутренняя точка |
||||||||||||
множества |
, т.е. |
входит в множество |
|
вместе с некоторой своей окрестностью: |
|
|||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|
, тогда величина |
|
|
|
называется приращением аргумента |
|
|||||||||
(приращением независимой переменной) в точке , а величина |
|
называется |
||||||||||||||
приращением функции (приращением зависимой переменной) в точке |
. Обозначения: |
|||||||||||||||
|
|
|
|
- приращение аргумента; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
- приращение функции. |
|
||||||
Приращения аргумента и функции могут принимать любые значения |
|
|||||||||||||||
(положительные, отрицательные или нулевые). |
|
|
|
|
|
|||||||||||
Поведение функции |
|
в окрестности точки можно описать |
качественно |
или |
||||||||||||
количественно , если известна некоторая зависимость приращения функции от |
|
|||||||||||||||
приращения аргумента |
. Например, если |
|
|
|
при |
|
, то функция |
|
||||||||
является непрерывной в точке . |
|
|
|
|
|
|
|
|
|
|
|
|||||
Для более точной характеристики поведения функции |
в окрестности точки |
|
||||||||||||||
служит понятие производной одно из фундаментальных понятий в математическом |
|
|||||||||||||||
анализе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. Если существует предел |
|
|
|
(конечный или бесконечный), то этот |
||||||||||||
предел называется производной функции |
|
|
|
в точке |
и обозначается |
: |
|
|||||||||
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если производная функции |
вычисляется в произвольной точке |
, то |
||||||||||||||
применяется формула: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
где |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
; |
|
; |
в частности: |
. |
|
||||||
|
|
|
|
|
|
|||||||||||
2. ;
;
; .

4
3. |
, |
; |
;
; |
. |
4. ; ;
; |
|
. |
5. |
|
если |
; |
; |
|
||||
|
|
если
не существует; |
. |
6. |
|
если |
; |
; |
|
||||
|
|
если
|
|
|
|
|
|
|
|
; |
. |
Геометрический смысл производной. |
|
|
|
||||||
|
|
|
|
|
|
||||
Рассмотрим на плоскости некоторую кривую |
и точку , лежащую на этой |
||||||||
кривой. Проведем секущую через точку |
и через другую точку , также лежащую на |
||||||||
кривой . Далее перемещаем точку вдоль кривой |
, неограниченно приближая к точке |
||||||||
(см. рис.) |
|
|
|
|
|
|
|||
 секущая
секущая
касательная
Определение. Предельное положение секущей |
при неограниченном приближении |
|||||
точки |
вдоль кривой к точке |
называется касательной к кривой в точке . |
||||
|
Используя понятие касательной, сформулируем геометрический смысл |
|
||||
производной. |
|
|
|
|
|
|
|
Для этого рассмотрим график |
непрерывной функции |
и точку |
, ), |
||
где |
. Проведем секущую |
|
и касательную к графику |
в точке |
. Пусть |
|
угол между секущей и осью |
, |
угол между касательной и осью , |
|
|||
угловой коэффициент касательной |
|
. |
|
|
||
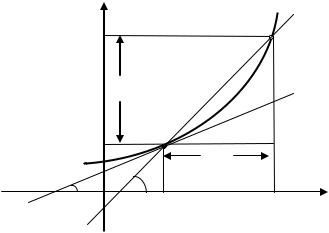
5
секущая
касательная
Из рисунка видно, что |
. |
При |
точка |
неограниченно |
|
|
||||
приближается к точке |
вдоль графика |
и, следовательно, секущая |
переходит в |
|||||||
пределе в касательную. При этом |
|
и |
. |
|
|
|
|
|||
Если |
существует, то |
|
|
|
|
|
. |
|
||
Таким образом, производная функции |
в точке |
равна угловому |
|
|
||||||
коэффициенту касательной, проведенной к графику функции в точке |
: |
|||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
Уравнение касательной: |
|
|
или: |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
|
Уравнение нормали: |
|
|
|
|
|
или: |
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Пример 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Составим уравнения касательной и нормали к графику функции |
|
в точке |
. |
||||||||||||||||||
|
Здесь |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
Уравнение касательной: |
|
|
|
|
|
|
или |
|
|
|
|
. |
|
|
|
|
|
||||
Уравнение нормали: |
|
|
|
|
|
|
или |
|
|
|
|
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Из геометрического смысла производной следует: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
; |
|
|
|
|
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
В случае |
имеем горизонтальную касательную с уравнением: |
|
|
|||||||||||||||||
и вертикальную нормаль с уравнением: |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
В случае |
имеем вертикальную касательную с уравнением: |
|
и |
|||||||||||||||||
горизонтальную нормаль с уравнением: |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
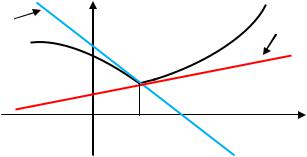
Пример 8. Для функции |
|
|
|
|
в точке |
имеем |
|
|
|
|
|
см Пример |
, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
поэтому касательная к графику функции в этой точке будет вертикальной |
и |
||||||||||||||||||||
будет совпадать с осью |
, а нормаль будет горизонтальной |
|
и будет совпадать с |
||||||||||||||||||
осью |
см рис |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

6
касательная
нормаль
Физический смысл производной.
1. Скорость и ускорение движения (механический смысл производной).
Пусть |
путь, пройденный материальной точкой за время при |
|
прямолинейном движении. Тогда |
- путь, пройденный за время . |
|
Отношение |
средняя скорость движения на этом промежутке. |
|
Чем меньше , тем точнее средняя скорость выражает скорость движения точки в
данный момент времени . |
|
|
|
|
|||
Скоростью движения точки в момент времени |
(или мгновенной скоростью) |
||||||
называется предел средней скорости движения при стремлении к нулю промежутка |
|||||||
времени |
|
|
|
|
|
|
. |
Таким образом, скорость прямолинейного движения материальной точки в |
|||||||
момент времени есть производная пути |
по времени : |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||
Аналогично устанавливается, что ускорение |
прямолинейного движения |
||||||
материальной точки в момент времени |
есть производная скорости по времени : |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
2. Сила тока. |
|
|
|
|
|
|
|
Пусть |
количество электричества, протекающего через поперечное |
||||||
сечение проводника за время . Тогда |
|
|
|
- количество электричества, |
|||
протекающего за время . Отношение |
|
|
средняя сила тока за промежуток . |
||||
Силой тока в момент времени называется предел средней силы тока при |
|||||||
стремлении к нулю промежутка времени |
|
|
|
. |
|||
Таким образом, сила тока в момент времени |
есть производная количества |
||||||
электричества |
по времени : |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
3. Теплоемкость тела. |
|
|
|
|
|
||
Пусть |
|
количество тепла, необходимого при нагревании тела от до |
|||||
температуры |
. Тогда |
|
|
- количество тепла, необходимого при |
|||
нагревании тела на температуру |
. Отношение |
средняя теплоемкость при |
|||||
нагревании от |
до |
. |
|
|
|
|
|
Теплоемкостью тела при температуре |
называется предел средней теплоемкости |
||||||
при стремлении к нулю величины |
|
|
|
|
. |
||
Таким образом, теплоемкость тела при температуре |
есть производная |
||||||
количества тепла |
по температуре |
: |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Обобщая вышеприведенные примеры, можно сформулировать физический смысл |
|||||||
производной: |
|
|
|
|
|
|
|
если функция |
описывает какой-либо физический процесс, то ее |
||||||
производная |
есть |
|
скорость |
протекания этого процесса. |
|||
Односторонние производные.
Если в определении производной функции ограничиться лишь значениями (справа от точки ), то получим определение производной справа (правосторонней
производной); если ограничиться лишь значениями |
(слева от точки |
), то |
||||
получим определение производной слева (левосторонней производной): |
|
|
||||
|
|
; |
|
|
|
. |
|
|
|
|
|||
Очевидно, что для существования «обычной» конечной производной необходимо и достаточно, чтобы существовали конечные производные справа и слева и они были бы равны:
|
|
|
|
. |
|
Если |
, |
, но |
|
, то |
не существует. |
В этом случае касательная к графику функции |
в точке |
также не существует, но в |
|||
этой точке есть левосторонняя и правосторонняя касательные (см. рис.) При этом точка на графике называется угловой точкой.
левосторонняя |
|
касательная |
правосторонняя |
|
касательная |
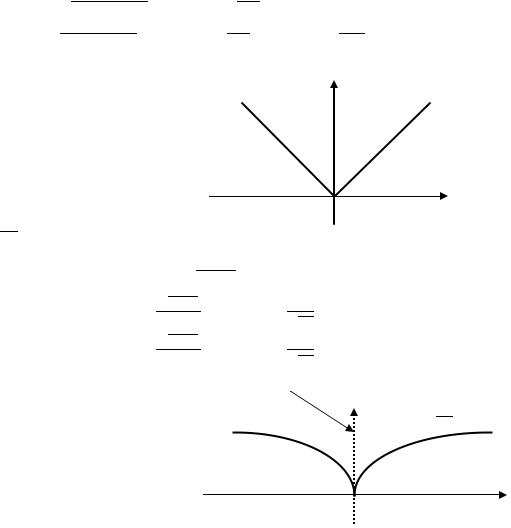
|
|
|
|
8 |
В случае бесконечных значений производных справа и слева имеем следующую |
|
|||
картину: |
|
|
|
|
- если |
и |
, то и |
; |
|
- если |
и |
, то и |
. |
|
В этих случаях касательная к графику в точке |
является вертикальной (см. Пример 8). |
|
||
Если |
, |
, или |
, |
, |
т.е. |
, то в этом случае |
|
, при этом левосторонняя и |
|
правосторонняя касательные вертикальны и совпадают (см. Пример ниже).
Примеры.
9. .
;
.
Так как |
, то |
не существует. |
Геометрически это означает, |
|
|
что в точке |
касательная к графику |
|
функции |
не существует. |
|
10. .
;
;
;
|
|
. |
касательная |
Здесь левосторонняя и правосторонняя |
|
||
касательные вертикальны и совпадают. |
|
||
Замечание. |
|
|
|
В определении производной функции |
в некоторой точке предполагалось, |
что |
внутренняя точка области определения |
. Теперь можно допустить, что эта |
точка не является внутренней для , но при обязательном условии, чтобы множество
содержало некоторый промежуток вида |
или |
, где |
. Тогда |
производная в точке будет пониматься как односторонняя производная. |
|
||

9
§ 2. Производные основных элементарных функций.
Вычислим производные основных элементарных функций.
1. Постоянная функция: |
. |
;
; .
2. Степенная функция. Частные случаи.
2.1. |
, |
натуральное число . |
. По формуле бинома Ньютона имеем:
;
;
;
.
Например: |
; |
; |
. |
2.2. .

 .
.
2.3. .

 .
.
Замечание. При имеем касательная
правостороннюю производную:
.

10
3. Степенная функция. Общий случай: |
, |
. |
|
|
|
||||||
3.1. |
; |
|
|
|
|
|
|
|
|
|
; |
|
|
при |
; |
|
|
|
|
||||
|
|
|
|
|
|
|
|
. |
|
|
; |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.2. |
; в этом случае |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
|
|
|
|
|
|
|
|
|
|
|
если |
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
если |
|
Например: |
|
; |
|
|
. |
|
|
||||
4. Показательная функция: |
|
, где |
. |
||
|
|
|
; |
|
|
|
|
при |
; |
|
|
;
|
|
|
|
|
|
|
; в частности: |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||
5. Логарифмическая функция: |
, где |
. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
при |
; |
|
|
|
|
|
|
|
|
|
|
; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
; в частности: |
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6. Тригонометрические функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6.1. |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
при |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
