ИЭ / 2 семестр / Учебник / Мат. анализ 1

91

§2. Основные методы интегрирования.

Косновным методам интегрирования относятся:

метод непосредственного интегрирования;

метод замены переменной;

метод интегрирования по частям.

1. Непосредственное интегрирование.

Этот метод состоит в применении основной таблицы интегралов и правил интегрирования путем тождественных преобразований с использованием известных формул элементарной математики. Рассмотрим примеры.

Пример 1.

.

Пример 2.

.

Пример 3.

.

Пример 4.

;

Пример 5.

.

92

Пример 6.

;

.

2. Замена переменной (метод подстановки или подведения под знак дифференциала).

Метод замены переменной основан на следующем факте.

дифференцируемая функция, то это равенство остается верным, т.е. , или иначе:

формула замены переменной.

Это следует из равенства:

.

Частным случаем этой формулы является линейная замена переменной:

.

Формула замены переменной может применяться в следующем виде:

, или:

,

такой метод называется еще подведением под знак дифференциала.

Например:

;

.

93

Применение формулы замены переменной возможно и в следующей форме (метод подстановки):

Например:

.

Замену переменной в неопределенном интеграле можно применять в тех случаях, когда невозможно непосредственное интегрирование. В случае «удачной» замены исходный интеграл сводится к табличному интегралу или к интегралу, к которому можно применить непосредственное интегрирование.

Общих методов подбора нужной замены переменной не существует. Лишь в отдельных случаях можно дать рекомендации, облегчающие поиск нужной замены переменной. Умение подобрать подходящую замену приходит с опытом и приобретается упражнениями и практикой.

Случаи, когда можно рекомендовать подходящую замену переменной, связаны с известными формулами для дифференциалов:

Рассмотрим некоторые интегралы, в которых встречаются эти выражения для дифференциалов, и укажем нужную замену (подстановку) переменной.

; и т.д.

Например:

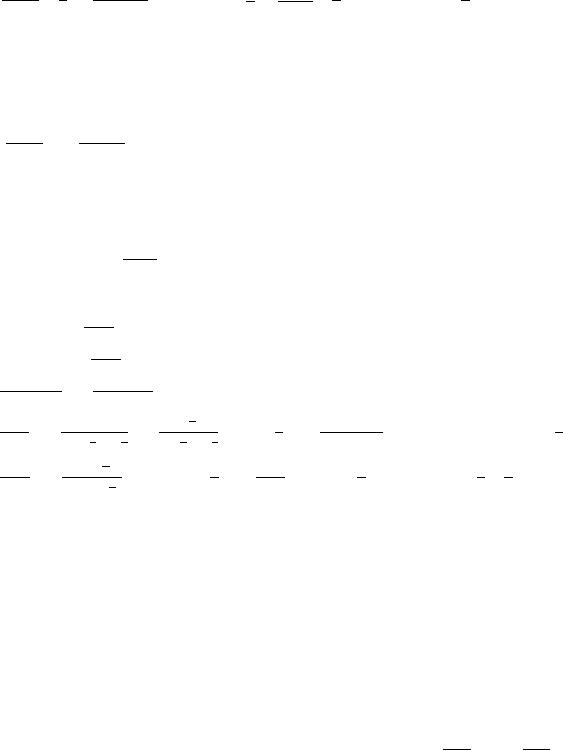
94

.

Например:

.

;

.

Например:

;

;

;

;

.

В общем случае, если непосредственное интегрирование к результату не приводит, то можно рекомендовать тригонометрические или гиперболические подстановки:

, ,

.

При этом используются известные соотношения между этими функциями:

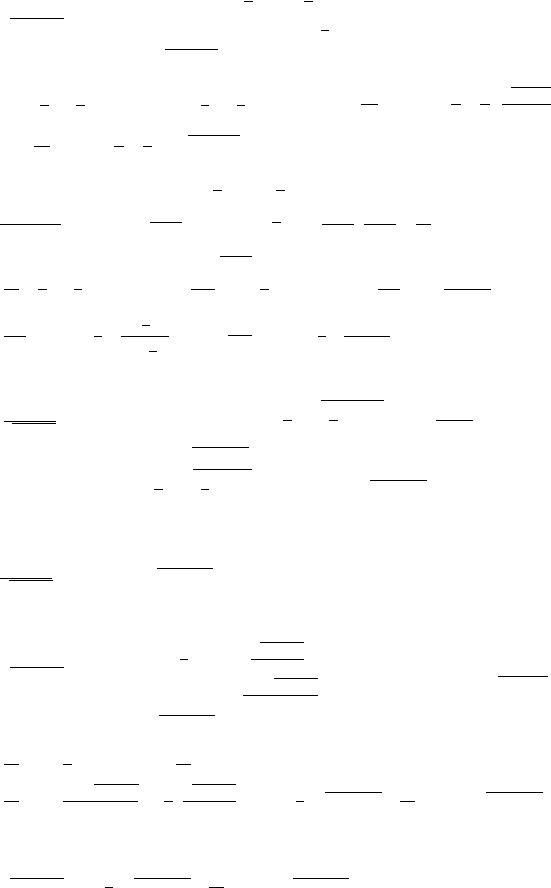
95

Например:

.

;

.

Аналогично можно показать, что

.

.

Аналогично можно показать, что

.

Например:

97

Иногда при вычислении интегралов приходится применять формулу

интегрирования по частям несколько раз.

Например:

.

В некоторых случаях после применения формулы интегрирования по частям получается исходный интеграл. В этих случаях полученное равенство нужно рассматривать как уравнение относительно неизвестного интеграла и решить его.

Отметим, что метод интегрирования по частям имеет более ограниченную область применения, чем метод замены переменной. Но есть интегралы, которые вычисляются именно методом интегрирования по частям. Эти интегралы можно условно разбить на следующие 3 типа:

98

) интегралы, у которых подынтегральная функция содержит в качестве множителя одну из следующих функций:

… ;

;

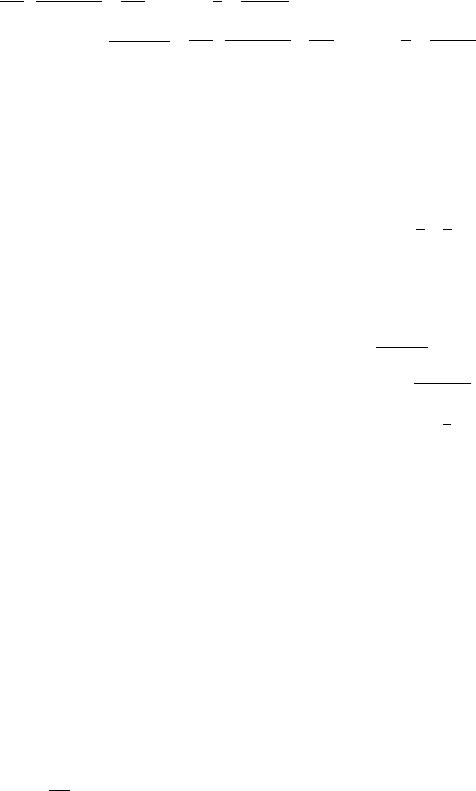
99

, или:

и т.д.

В заключение дополним основную таблицу интегралов некоторыми полученными здесь формулами, имеющими широкое применение в приложениях.

Дополнение к основной таблице интегралов.

§ 3. Интегрирование рациональных функций.

«Берущиеся» и «неберущиеся» интегралы.

В дифференциальном исчислении было показано, что производная любой элементарной функции также является элементарной функцией, т.е. операция дифференцирования не выводит за пределы множества элементарных функций.

С операцией интегрирования дело обстоит уже иначе. Есть элементарные функции, для которых их первообразная не является элементарной функцией, т.е. не выражается через основные элементарные функции с помощью арифметических действий и суперпозиции этих функций.

Наиболее известными примерами таких интегралов могут служить следующие:

-интегральный логарифм;

Хотя эти интегралы и существуют, как интегралы от непрерывных функций, но они не выражаются через элементарные функции. Такого типа интегралы называются

100

«неберущимися» интегралами. В отличие от них все остальные интегралы называются «берущимися» интегралами.

Существует не так много классов элементарных функций с «берущимися» интегралами, т.е. классов функций, для которых интегрирование может быть выполнено в конечном виде и привести обязательно к какой-нибудь элементарной функции.

Среди таких классов функций на первом месте по значению стоит класс

Здесь необходимо напомнить некоторые сведения об алгебраических многочленах и рациональных функциях (см. , глава 7).

Рациональные функции.

Рациональной функцией, как известно, называется отношение двух многочленов:

Любой многочлен можно разложить на линейные и квадратичные множители с вещественными коэффициентами:

,

Условие: - означает, что квадратичные множители не имеют действительных корней, и они уже не могут быть разложены в произведение линейных множителей с вещественными коэффициентами.

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя , в противном случае дробь называется

неправильной.

Если рациональная дробь неправильная, то ее можно представить в виде суммы многочлена и правильной рациональной дроби, используя операцию деления с остатком. Это действие называется выделением целой части из дроби.

Например:

;

Среди правильных дробей выделяют так называемые простейшие дроби.