11.Метод перемены плоскостей проекции

11. Метод перемены плоскостей проекций

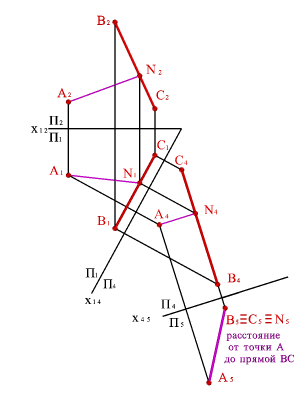
Перемена плоскостей может помочь при нахождении натуральных величин отрезков.

Изменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П1 или П2 новой плоскостями П4. Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.

Для решения некоторых задач может потребоваться двойная замены плоскостей проекций. Последовательный  переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

12.Пересечение многогранников плоскостью и прямой

Для построения точек пересечения отрезка прямой с поверхностью многогранника, также как в задаче о пересечении прямой и плоскости, необходимо через заданную прямую провести вспомогательную плоскость частного положения и определить сечение заданной поверхности проведенной плоскостью. Точки, в которых прямая пересечется с сечением, будут искомыми точками пересечения прямой с поверхностей многогранника.

1. Через прямую m проведем фронтально-проецирующую плоскость α. 2. Плоскость α пересекает ребра пирамиды Ф в точках 1,2,3. (1-2-3) = α ∩ Φ.

3. Прямая m пересекается с сечением (1-2-3) в точках I, II, которые являются искомыми. I, II = m ∩ (1-2-3).

4. Видимость прямой m в проекциях определяем способом конкурирующих точек. Поверхность пирамиды рассматриваем как непрозрачную оболочку.

Форма многоугольника, полученного при сечении многогранника плоскостью, зависит от ее положения относительно основания многогранника. Секущая плоскость может быть параллельна, перпендикулярна или наклонена к основанию многогранника. В первом случае фигура сечения будет равна (для призмы) или подобна (для пирамиды) основанию.

Когда секущая плоскость не параллельна ни одной из плоскостей проекций, фигура сечения проецируется с искажением. Поэтому, если требуется определить натуральный вид сечения, то следует применять один из способов преобразования проекций.

Для построения линии пересечения многогранника плоскостью общего положения необходимо преобразовать способом замены плоскостей проекций заданную плоскость в проецирующую. Для этого выбирается новая плоскость проекций, перпендикулярная данной плоскости и строится новый след плоскости (если она задана плоской фигурой, то – новая проекция этой фигуры) и новая проекция многогранника. Относительно плоскостей проекций заданная плоскость станет проецирующей и задача решается как в приведенном примере.

1. фронтальная проекция плоской фигуры сечения - отрезок прямой линии. Обозначаем ее вершины - А₂=D₂, В₂, С₂ – точки пересечения плоскости α с ребрами призмы.

2. Для построения их горизонтальных и профильных проекций достаточно провести соответствующие линии проекционной связи, так как грани призмы и плоскость α занимают частные положения. Дополнительную линию проводим лишь при построении профильной проекции точки А.

 3. Строим линии пересечения граней призмы с плоскостью α, т. е. проекции четырехугольника АBCD. Определяем видимость тех его сторон, изображения которых не совпадают с проекциями граней пирамиды.

4. Фигура сечения изображена на основных плоскостях проекций с искажением. Ее истинную величину получаем проецированием на дополнительную плоскость, параллельную плоскости α, выполняя замену плоскостей проекций.