7.Виды многгранников

Куб, шар, пирамида, цилиндр, конус — геометрические тела. Среди них выделяют многогранники. Многогранникомназывают геометрическое тело, поверхность которого состоит из конечного числа многоугольников. Каждый из этих многоугольников называется гранью многогранника, стороны и вершины этих многоугольников — соответственно ребрами и вершинами многогранника.

Двугранные углы между соседними гранями, т.е. гранями, име­ющими общую сторону — ребро многогранника — являются так­же и двугранными умами многогранника. Углы многоугольников — граней выпуклого многоугольника — являются плоскими умами многогранника. Кроме плоских и двугранных углов у выпуклого многогранника имеются еще и многогранные углы. Эти углы образу­ют грани, имеющие общую вершину.

Среди многогранников различают призмы и пирамиды.

Призма — это многогранник, поверхность которого состоит из двух равных многоугольников и параллелограммов, имеющих об­щие стороны с каждым из оснований.

Два равных многоугольника называются основаниями ггризмьг, а параллелограммы — ее боковыми гранями. Боковые грани образуют боковую поверхность призмы. Ребра, не лежащие в основаниях, называются боковыми ребрами призмы.

Призму называют п-угольной, если ее основаниями являются я-угольники. На рис. 24.6 изображена четырехугольная призма АВСDА'В'С'D'.

Призму называют прямой, если ее боковыми гранями являются прямоугольники (рис. 24.7).

Призму называют правильной, если она прямая, а ее основа­ния — правильные многоугольники.

Четырехугольную призму называют параллелепипедом, если ее основания — параллелограммы.

Параллелепипед называют прямоугольным, если все его грани — прямоугольники.

Диагональ параллелепипеда — это отрезок, соединяющий его противоположные вершины. У параллелепипеда четыре диаго­нали.

 

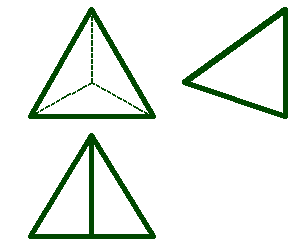
 Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники  с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью (рис.67).

а) модель		б) эпюр
Рисунок 67. Пирамида

2. Призма - многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы. Призма называется прямой, если её ребра перпендикулярны плоскости основания. Если основанием призмы является прямоугольник, призму называют параллелепипедом (рис. 68).

а) модель		б) эпюр
Рисунок 68.  Призма

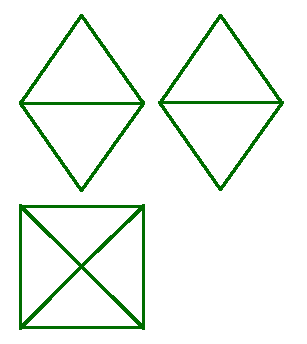
3. Призматоид - многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники или трапеции, вершины которых являются и вершинами  многоугольников оснований (рис.69).

а) модель		б) эпюр
Рисунок 69. Призматоид

4.   Тела Платона.  Многогранник, все грани которого  представляют собой правильные и равные многоугольники, называют правильными. Углы при вершинах такого многогранника равны между собой.

Существует пять типов правильных многогранников. Эти многогранники и их свойства были описаны более двух тысяч лет назад древнегреческим  философом Платоном, чем и объясняется их общее название.

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

Тетраэдр - правильный четырехгранник (рис.70). Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).

а) модель			б) эпюр
Рисунок 70. Тетраэдр

Гексаэдр - правильный шестигранник (рис. 71). Это куб состоящий из шести равных квадратов.

а) модель		б) эпюр
Рисунок 71. Гексаэдр

Октаэдр - правильный восьмигранник (рис.72). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.

а) модель		б) эпюр
Рисунок 72. Октаэдр

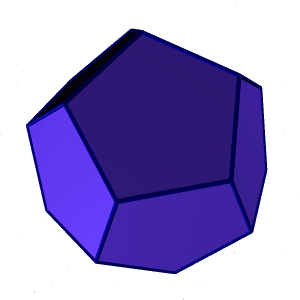
Додекаэдр - правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины (