6.Основные позиционные задачи

Основными позиционными задачами называются задачи на определение взаимного расположения точки, прямой и плоскости.

Для видимости на чертеже применяется метод конкурирующих точек. Конкурирующими называются точки, расположенные на одной проецирующей прямой. На рисунке 4.1 (АВ) ^П₁, следовательно точки А и В – фронтально-конкурирующие. (СD) ^П₂, поэтому точки С и D – горизонтально-конкурирующие. Точка С находится выше точки D, поэтому точка С является видимой на горизонтальной проекции. Ордината точки Абольше, чем точки В, поэтому точка А находится ближе к зрителю, следовательно, она является видимой на фронтальной проекции.

Прямые и точки, лежащие в плоскости. Прямая принадлежит плоскости, если две ее точки принадлежат данной плоскости. На рисунке 4.2 показана прямая l, принадлежащая плоскости a(bÇc), поскольку имеет с нею две общие точки – В и С.

Точка принадлежит плоскости, если она расположена на прямой, принадлежащей данной плоскости. Для того чтобы построить в плоскости a(bÇc) точку K (рисунок 4.2), необходимо провести в плоскости прямую l, принадлежащую плоскости a(bÇc), а затем задать на ней точку K, которая принадлежит прямой l и, следовательно, плоскости a(bÇc).

Главные линии плоскости. Среди множества прямых, которые могут быть проведены в плоскости, следует выделить главные линии плоскости:

1. Горизонтали – прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций (рисунок 4.3а). Фронтальная проекция горизонтали горизонтальна.

2. Фронтали – прямые, принадлежащие плоскости и параллельные фронтальной плоскости проекций (рисунок 4.3б). Горизонтальная проекция фронтали горизонтальна.

 3. Линии наибольшего ската(наклона) — прямые, принадлежащие данной плоскости и перпендикулярные горизонталям (или фронталям) плоскости. На рисунке 4.4 показана линия наибольшего ската MN плоскости a.

Следует отметить, что следы плоскости также являются главными линиями плоскости – горизонталью и фронталью, совмещенными с плоскостями проекций. Главные линии плоскости в качестве вспомогательных прямых облегчают решение ряда задач.

 Взаимное положение двух плоскостей. Две плоскости в пространстве могут быть параллельными или пересекающимися. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым второй плоскости. Если параллельные плоскости задаются на эпюре следами, то одноименные следы этих плоскостей должны быть параллельны. На рисунке 4.5 плоскость a(aÇb) параллельна плоскости b(сÇd), поскольку с || а(с₁ || а₁, с₂ || а₂ ), d || b (d₁ || b₁, d₂ || b₂ ) .

 

Для построения точки пересечения прямой линии l с плоскостью a(АВС) необходимо(рисунок 4.9):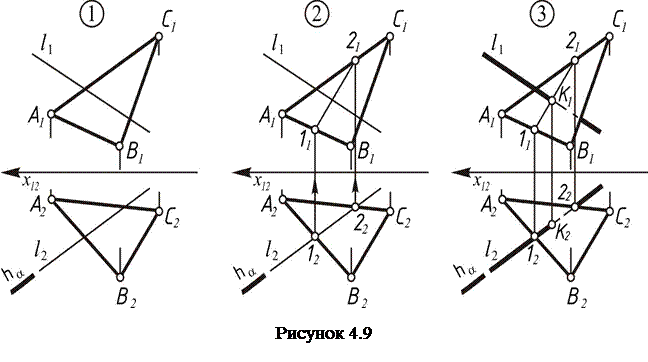 1) провести через прямую l вспомогательную проецирующую плоскость b; 2) построить линию MN пересечения данной плоскости a и вспомогательной плоскости b; 3) определить искомую точку К пересечения данной прямой l с линией пересечения плоскостей MN (в случае если l || MN, то прямая lпараллельна плоскости a, если l Î MN, то прямая l принадлежит плоскости a).