Зависимость видности полос от ширины d протяженного источника.

При 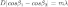(m=1,2,...) видность, как уже отмечалось, обращается в нуль. Ориентировочно в качестве условия хорошего наблюдения интерференционной картины от протяженного источника можно принять неравенство $D |cos{\beta_1}-cos{\beta_2}| \approx \lambda/2$. При его выполнении видность полос .

26) Интерференция в тонких плёнках. Вывод формулы для разности хода. Полосы равного наклона. Метод контроля плоскопараллельности пластин.

Примеры: радужные полосы на поверхности, радужная окраска мыльных пузырей, оперенья птиц, крылышек бабочек.

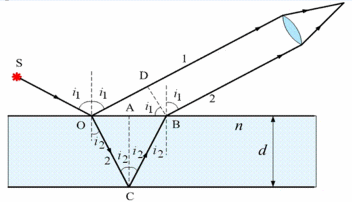
Рис. 26.1

Как возникают цвета тонких плёнок при освещении белым светом? Световая волна, падая на пластину, частично отражается (луч 1 на рис.26.1), частично преломляется. Преломлённый луч, отражаясь от нижней поверхности плёнки (луч 2 на рис.26.1), интерферирует с лучом 1, отражённым от верхней поверхности. Если эти лучи окажутся в противофазе, они погасят друг друга, и в отражённом луче не будет света с такой длиной волны. При падании света под другим углом разность хода будет другая, и лучи могут оказаться в одной фазе; тогда они усилят друг друга. Яркость плёнки в этом цвете возрастает.

Вычислим разность хода   лучей в тонкой плёнке с показателем преломления n и толщиной d при падении света под углом 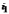 . Начиная от точки О, где луч раздваивается, разность хода набегает до точек D и B, лежащих на одном волновом фронте обоих лучей.

Первый луч проходит путь ОD в воздухе и теряет полволны при отражении от оптически более плотной среды в точке О; длина оптического пути его равна

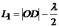. (26.1)

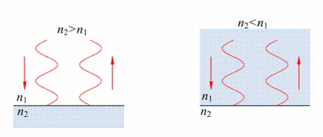
Рис. 26.2

Потерю полдлины волны при отражении иллюстрирует рис.26.2: фаза волны скачком меняется на противоположную при n2>n1 и не изменяется при n2<n1.

Второй луч проходит путь ОСВ в среде с показателем преломления n и, отражаясь от оптически менее плотной среды в точке С, полволны не теряет. С учётом того, что

,

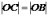длина оптического пути второго луча равна

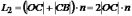. (26.2)

Из прямоугольных треугольников ОDB и OAC:

;  .

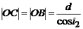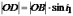По закону преломления в точке О:

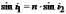. (26.3)

Далее,

,

.

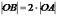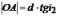Тогда оптическая разность хода

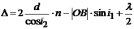
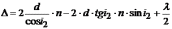
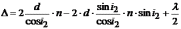
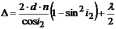
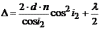
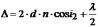
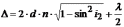
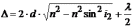
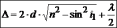 (26.4)

Условие минимума (18.7б) можно записать в виде:

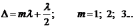 (26.5)

Тогда

.

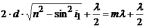
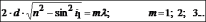Интерференционная картина определяется величинами  ,  ,  , .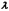

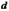При освещении светом плоскопараллельной пластинки (b  = const ) результаты интерференции зависят только от углов падения на плёнку. Интерференционная картина имеет вид чередующихся криволинейных тёмных и светлых полос. Каждой из этих полос соответствует определённое значение угла падения. Поэтому они называются полосами или линиями равного наклона. Если оптическая ось линзы L перпендикулярна к поверхности плёнки, полосы равного наклона должны иметь вид концентрических колец с центром в главном фокусе линзы. Это явление используется на практике для весьма точного контроля степени плоскопараллельности тонких прозрачных пластинок; изменение толщины пластинок на величину порядка 10^-8 м уже можно обнаружить по искажению формы колец равного наклона.

Формула (26.4) выведена для случая наблюдения интерференции в преломленном свете. Если интерференционные полосы равного наклона наблюдаются в тонких пластинках или плёнках, находящихся в воздухе на просвет (в проходящем свете), то потери волны при отражении не происходит. Следовательно, оптические разности хода для проходящего и отражённого света отличаются на λ/2, т.е. максимумам интерференции в отражённом свете соответствуют минимумы в проходящем свете, и наоборот.